




尽管随着移动通信技术这些年的迅猛发展,地面通信网络在世界范围内已覆盖了多数人群,但在人迹罕至的沙漠、高山、海洋、极地地区等,尚有大面积的覆盖空洞,而卫星通信可以有效地为这些地区提供无线服务。与地面通信中的固定基站/低功率节点不同,除了距离地球表面35786 km的同步卫星(GEO),其他大部分卫星,无论是高度在8000~20000 km的中轨卫星(MEO),还是高度在500~2000 km的低轨卫星(LEO),如图3-21所示,都是沿着地球的大圆,环绕地球(地心)公转,也就是说中轨卫星或者低轨卫星基站/中继节点相对于地面始终是运动的,是一个不断运动漂移的网络。
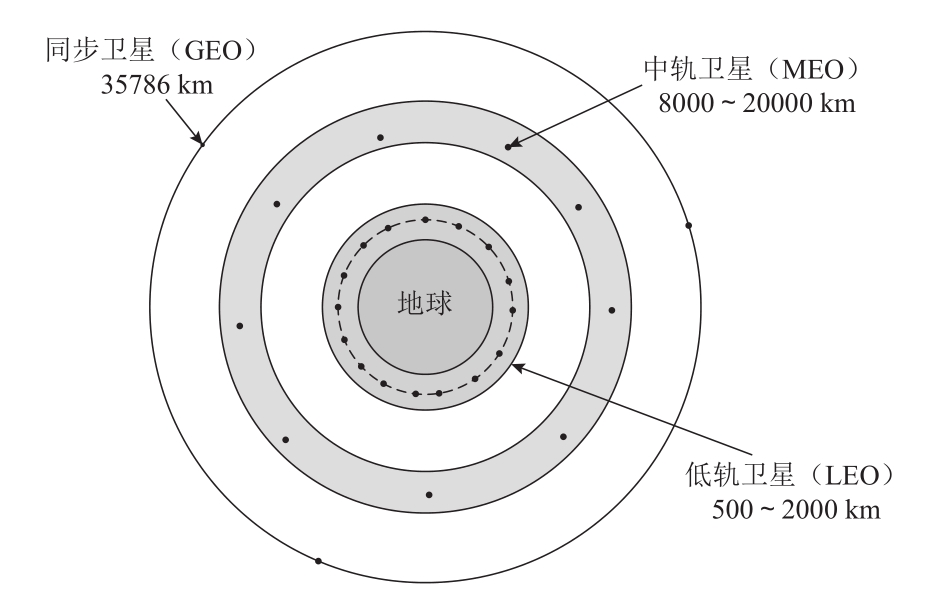
图3-21 通信卫星按高度分类的示意图(圆形轨道为例)
对于同一条轨道上的卫星,它们之间的相对距离基本保持不变(但不一定等距),周期性地对地球上某一地区的用户提供服务。当部署的卫星数量达到一定程度时,业务的连续性可以通过切换至同一轨道相邻的卫星或者邻近轨道上的卫星或更高轨的卫星得以保障。根据运动学原理和万有引力定律,得

式中, M 和 m 分别是地球和卫星的质量, M = 5.965×10 24 kg; v 是卫星环绕地球的线速度; G 是万有引力常数,等于6.67×10 -11 Nm 2 /kg 2 。因此,环绕速度可以表示为

可见,轨道越低,卫星环绕速度越快(例如,对于600 km、1500 km和10000 km高度,速度分别是7.5622 km/s、7.1172 km/s和4.9301 km/s),环绕周期越短,对地面的视角越大,卫星切换越频繁。低轨卫星的优势在于:①传输时延较小;②路径损耗较小;③可以更密集地覆盖地球表面。这些都可以大大提高卫星-地面一体化网络的容量。
卫星与地面用户的基本路径损耗(不包括空气吸收、电离层/平流层闪烁、穿透损耗)可以用以下公式表示:
FSPL( d , f c )=32.45+20lg( f c )+20lg( d ) (3-8)
式中,载频 f c 的单位是GHz;与地面用户的距离 d 的单位是m。尽管在自由空间传播,但由于传输距离很长,路径衰减还是相当严重的。以S波段的2 GHz载频为例,对于低轨600 km和1200 km的基本路径损耗分别为154 dB和160 dB。这个损耗比相距为300 m的两个地面终端之间的路损还高。如果是Ka波段的20 GHz载频,低轨600 km和1200 km的路径损耗分别可达174 dB和180 dB。
相比正常工作条件下,sub-6G频段的地面基站与用户的路损一般在100~130 dB的范围。为了弥补近30 dB的额外路损,通信卫星通常需要很大孔径的天线及大阵列单元形成方向可调的窄波束,从而满足地面目标用户的信号强度要求。随着星上天线的制造水平的进步,以及火箭运载能力的不断提升,即使是低轨的通信卫星,天线孔径目前可以做到直径超过5 m,能够支持手持式终端,大大增强了卫星通信的移动性。
由于卫星沿地球大圆环绕,尽管每条轨道上的卫星的相对位置比较固定,但相同高度的各个不同轨道上的卫星之间的相对位置是动态变化的,这些卫星不是按照某种固定队形做整体迁移。轨道的排布也有多种方式,即使是一个卫星网络中同样高度的卫星轨道,也可以与赤道平面呈不同角度,如图3-22所示。具体的轨道排布取决于所服务的地区、业务需求、覆盖连续性、每个轨道上的卫星数目、轨道高度等。
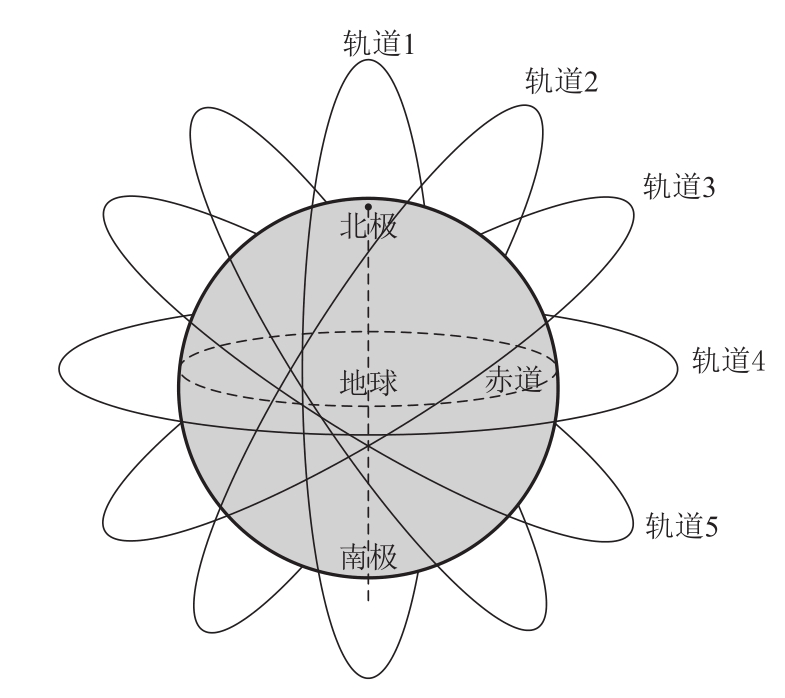
图3-22 相同高度的卫星轨道示意图(以圆形轨道为例)
环绕轨道可以是圆形的,也可以是椭圆形的。椭圆轨道上的卫星在远地点时的环绕速度最低,在近地点时的环绕速度最高,覆盖半径也不断变化,计算比较复杂。为方便分析,不失一般性,本节以圆形轨道为例。卫星正下方地面的波束覆盖半径 R B 与地球半径 R E 、卫星距离地面的高度 H 、3 dB的波束半角宽度 η 等的关系可以用以下公式表示。其中一些参数的几何关系如图3-23所示 [6] 。3 dB的波束半角宽度 η 与天线孔径 D 和波长 λ 之间的关系可以近似写成 η = 35 λ / D 。
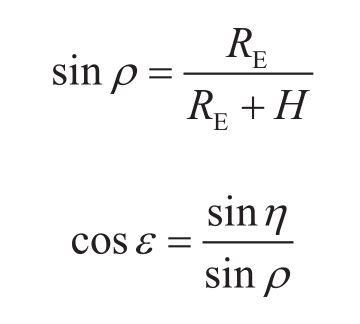

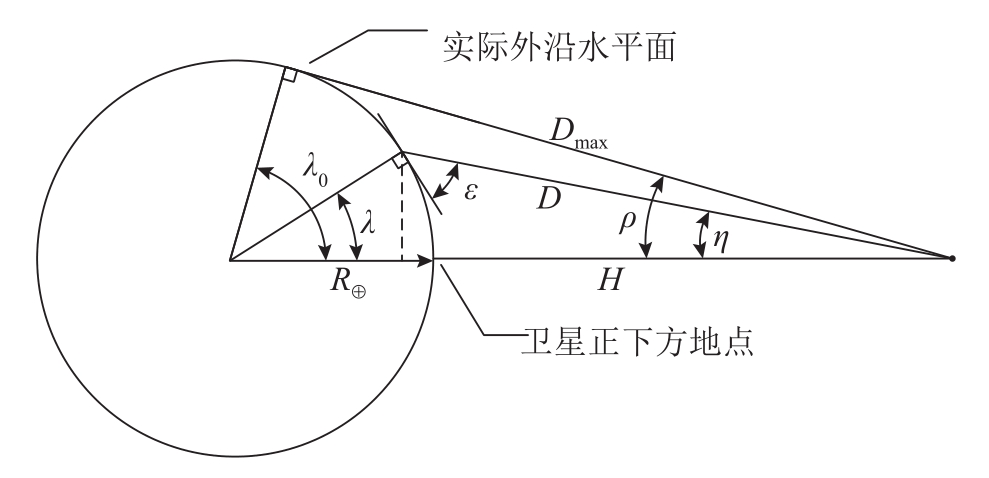
图3-23 计算卫星波束地面覆盖半径(在卫星正下方)
注: D —卫星与波束外沿的距离; D max —卫星与地平线的距离。
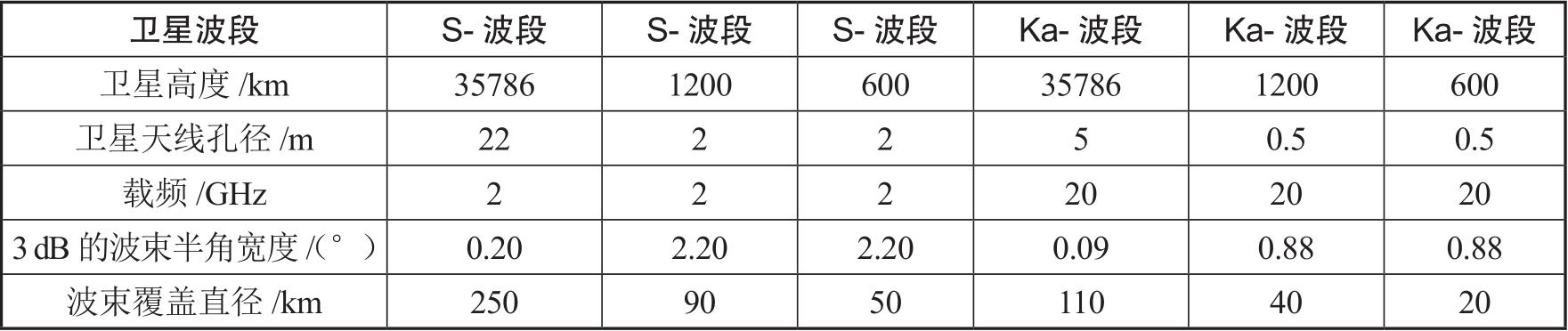
根据以上的波束覆盖半径公式,分别代入卫星高度、卫星天线孔径和波长,可以大致计算出在卫星正下方的波束覆盖直径,如表3-4所列。对于处于35786 km高度的S-波段同步卫星,天线孔径较大,可达22 m,波束较窄,只有12分(0.2°),但由于距离地面较远,尽管波束很窄,但一个波束的覆盖直径仍可达250 km;同样,S-波段距离地面1200 km和600 km的低轨卫星,典型的天线孔径为2 m,波束宽度虽增加了10倍,但覆盖直径分别只有90 km和50 km。以上的卫星工作在Ka波段时,天线孔径因为波长的减小可以适当减小,波束能够更细,覆盖直径也相应更小。例如,Ka波段的600 km高的低轨卫星,其波束覆盖直径只有20 km。
表3-4 典型卫星高度、天线孔径、载频、3dB的波束半角宽度和正下方波束覆盖直径 [7]
需要强调的是,以上的波束覆盖半径的计算是假设在卫星的正下方的区域,即波束的法线方向与地面垂直。然而,在很多时候,卫星与地面覆盖区域的俯仰角远小于90°,如图3-24所示。此时,每个波束覆盖区域在沿着卫星轨道方向的直径和垂直于卫星轨道方向的直径都变长,但前者变长更快、更显著,波束照到地面的“光斑”变成类似椭圆的形状。地球表面的球面形状使得“光斑变形”的现象更加明显,如图3-25所示。这里的低轨卫星工作在S波段,距离地面的高度为1200 km。卫星天线的总孔径为2 m。如果按照半波长的天线单元间距,即3×10 8 /(2×10 9 ×2)= 0.075(m),可以容纳(2/0.075) 2 = 711个单元。处理器通过对各个天线单元施加合适的预编码权值,形成331个波束。从图3-25可以看出,外圈波束“光斑”直径是中心光斑直径(即卫星正下方波束光斑直径)的3~4倍。由于卫星一直在运动,为了保障业务的连续性,需要不断地进行波束间的切换。对于1200 km高的S波段低轨卫星,最频繁时,大约每12(90/7.5)秒就需要切换一次服务波束。
从图3-24可以看出,斜角度入射加剧了一个波束覆盖区域内的传输时延差别,这尤其对随机接入有较大影响,对于卫星空口的传输,需要设计合理的前导信号结构。
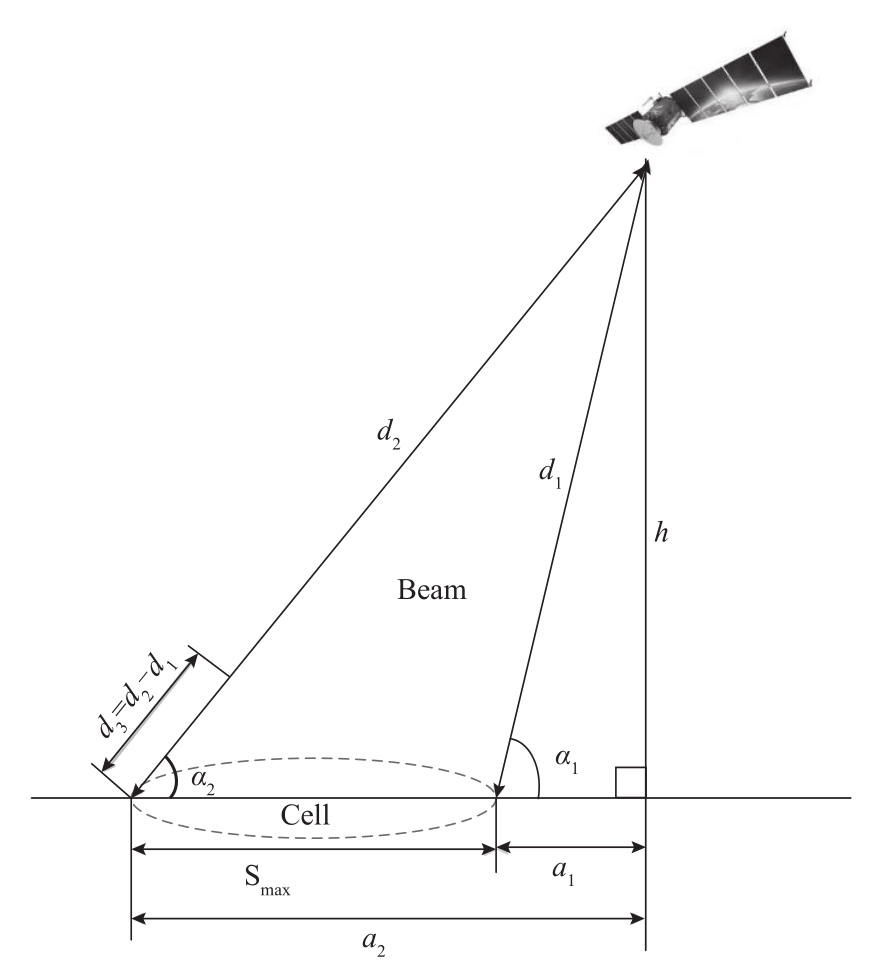
图3-24 斜入射波束的覆盖和路程差问题(假设地面为理想平面)
注: h —卫星距离地面的高度; d 1 、 d 2 —波束近边缘和远边缘距离卫星的距离; a 1 、 a 2 —波束近边缘和远边缘与卫星正下方地面点的距离;S max —波束直径; α 1 、 α 2 —卫星相对于波束近边缘和远边缘的俯仰角。
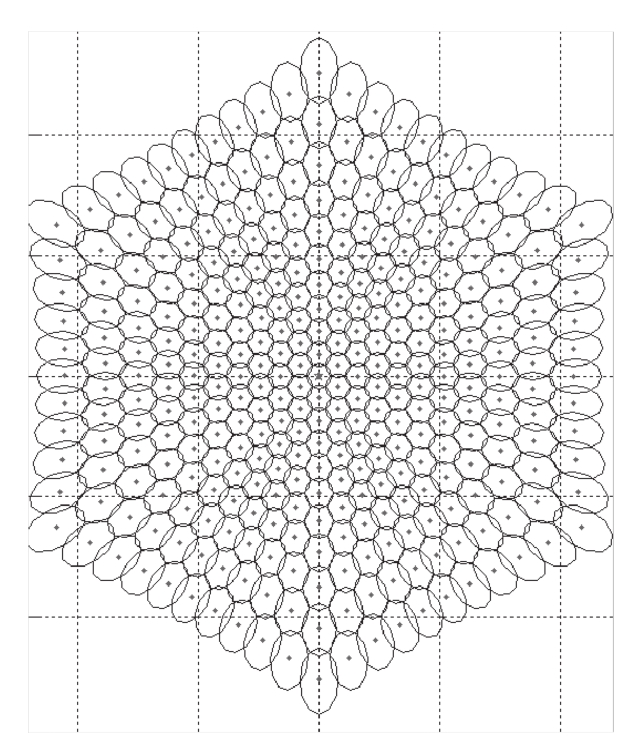
图3-25 一颗低轨卫星331个波束的覆盖范围示意(S波段1200km高度) [8]
从图3-25可以看出,一颗S波段1200 km高度的低轨卫星的整个覆盖半径大约是中心波束直径的14倍,即14×90=1260(km),接近于卫星的高度。类似的,600 km高度的低轨卫星的覆盖半径大致为600 km。地球大圆的周长为2×6400×3.14=40192(km),即一个600 km低轨轨道至少需要约34(40192/600/2)颗卫星来覆盖整个轨道对应的带状区域。轨道之间最宽处也近似为600×2=1200(km),即需要34条轨道保证足够的密度,因此总的卫星数至少是34×34=1156(颗)。在实际部署时,所需要的卫星数远比这个高,其中一个重要原因是图3-25中的比较靠外的波束对于地面用户的俯仰角较小,信道质量较差,波束半径又比较大,一个波束所能承载的数据传输速度较低,很难满足速率要求稍高的业务。只有在卫星正下方附近的波束才能支持较高速率。小俯仰角时,卫星-地面信道情况变化是由几个方面因素造成的。
第一个因素是俯仰角。小俯仰角卫星的多普勒频移较大。多普勒频移的计算如图3-26所示。影响多普勒频移的一个重要因素是SM向量与速度向量V的夹角,用 θ 来表示。这里的卫星高度为 h ,地球半径是 R ,载频是 F c 。多普勒频移的表达式为
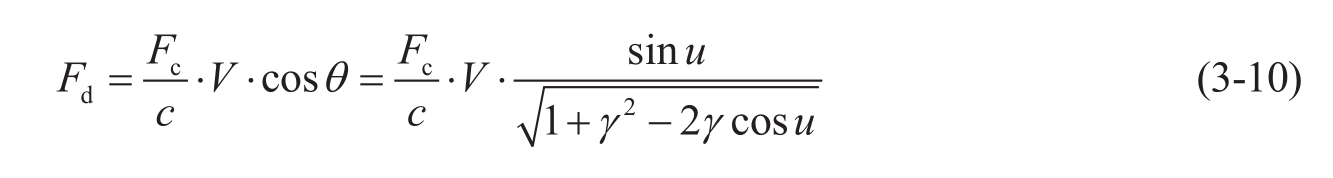
式中, u 是向量OM和向量OS的夹角,其中向量OM是地心指向地面用户,向量OS是地心指向卫星;角度 α 是卫星相对用户的俯仰角;常数 γ = ( R + h )/ R 。考虑600 km高度的卫星,载频为2 GHz,地面终端沿着卫星环绕方向或者相反方向以1000 km/h的速度行驶,根据式(3.10)可以计算在不同时刻[以min(分钟)为单位]的多普勒频移,如图3-27所示。在第0 min到第5 min,卫星俯仰角较小,多普勒频移保持在45 kHz左右;从第5 min到第8 min,卫星俯仰角较大,尤其在第6.5 min时,卫星在用户正上方,多普勒频移为0;第8 min之后,卫星俯仰角变小,多普勒频移趋近于-43 kHz。虽然多普勒频移的变化有解析公式表达,可以事先做处理且进行预处理补偿,但还是对接收机有负面影响。
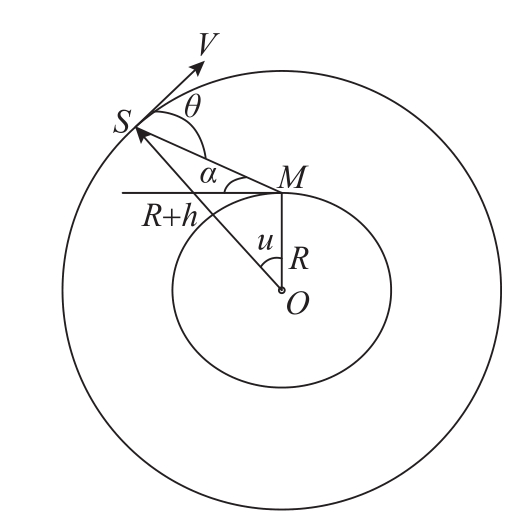
图3-26 卫星-地面通信多普勒频移的计算示意图
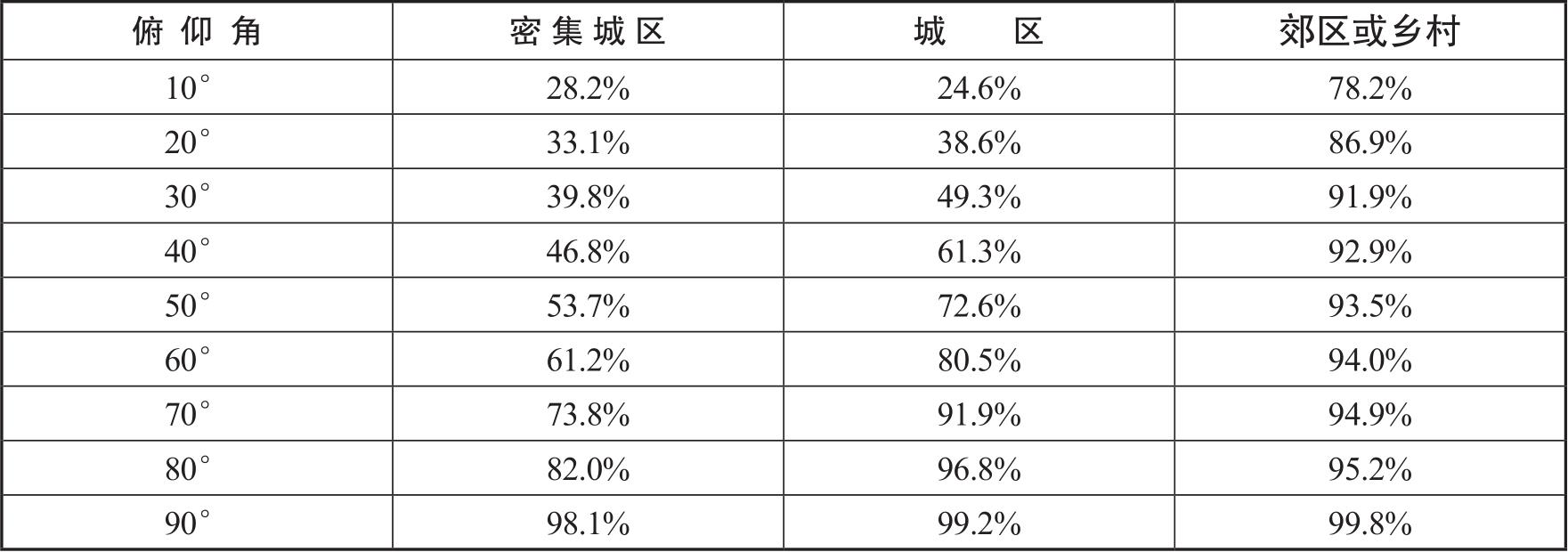
第二个因素是路损。除了基本的自由空间路损,卫星-地面信道的路损还包括阴影衰落和周围建筑物的杂物路损,而后面这两种额外路损与卫星-地面信道的视距(LOS)比例关系很大,LOS比例又直接取决于卫星的俯仰角,如表3-5所示,分别列举了密集城区、城区、郊区(乡村)3种场景下在俯仰角为10°~90°的LOS传播概率。在密集城区,由于高层建筑物密集,俯仰角在50°以下时,LOS传播只占一半左右;在一般城区,建筑物密度相对较低且高度有限,俯仰角在30°以下时,NLOS传播才明显;而在郊区或乡村,由于十分空旷,即使俯仰角在10°,LOS传播仍占主流。
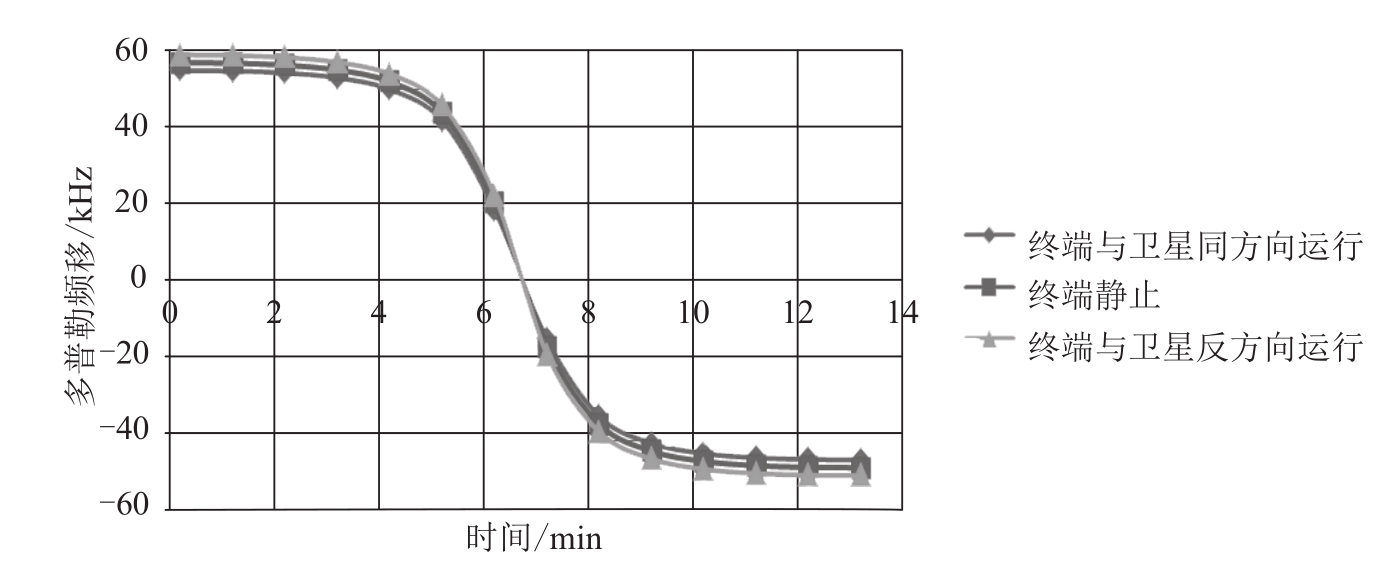
图3-27 工作在2GHz的600km低轨卫星-地面通信多普勒频移随时间的变化关系 [7]
表3-5 不同场景下,俯仰角与LOS传播概率的关系 [7]
如果传播链路不是LOS,周围建筑物会造成严重的阴影衰落和杂物路损(CL),如表3-6、表3-7和表3-8所示。
表3-6 密集城区场景的阴影衰落( σ SF )和杂物路损(CL)
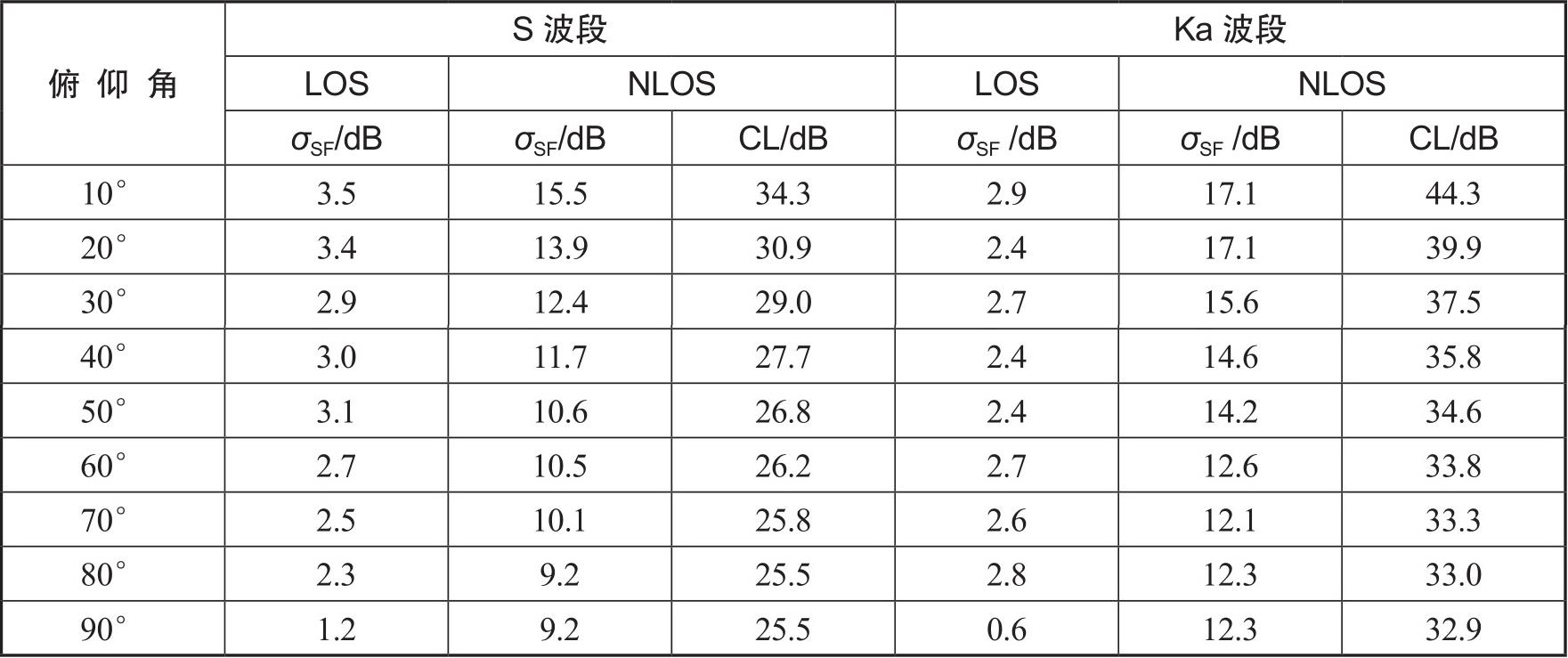
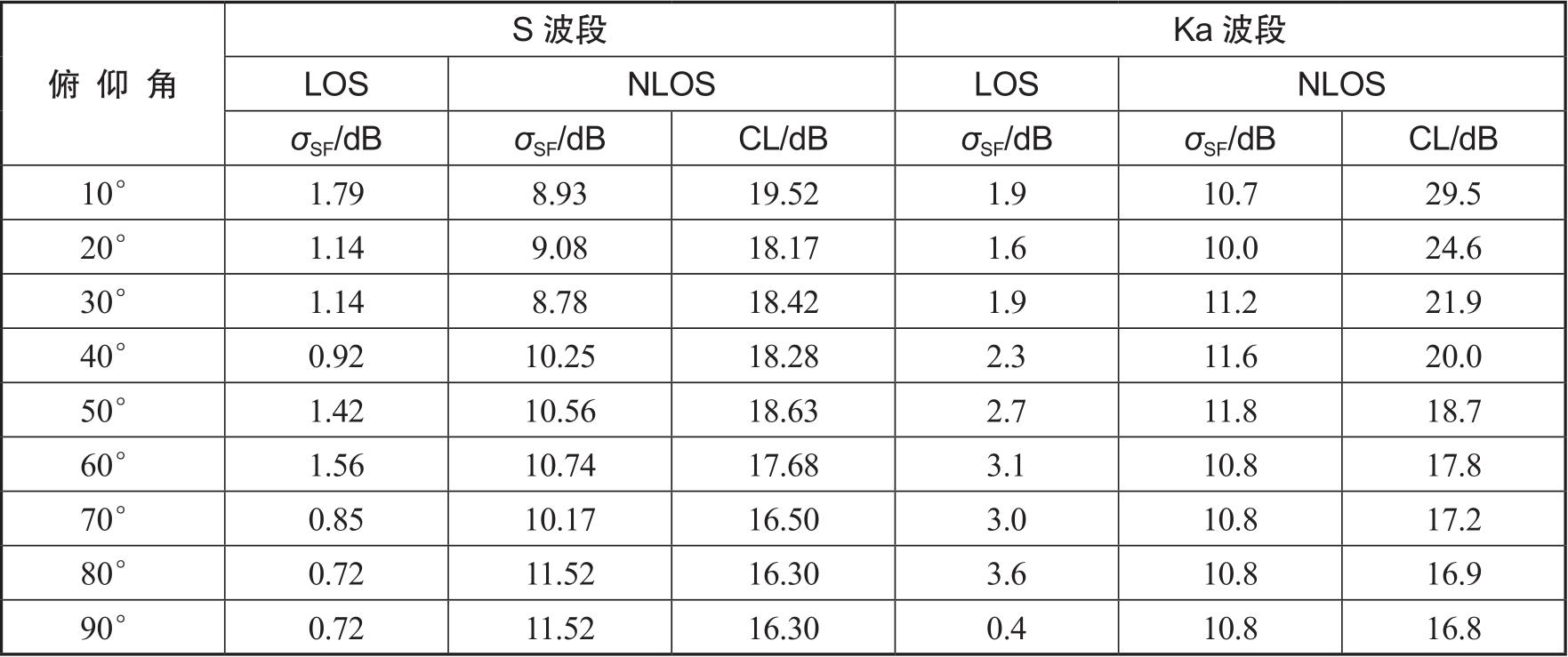
表3-7 城区场景的阴影衰落( σ SF )和杂物路损(CL)
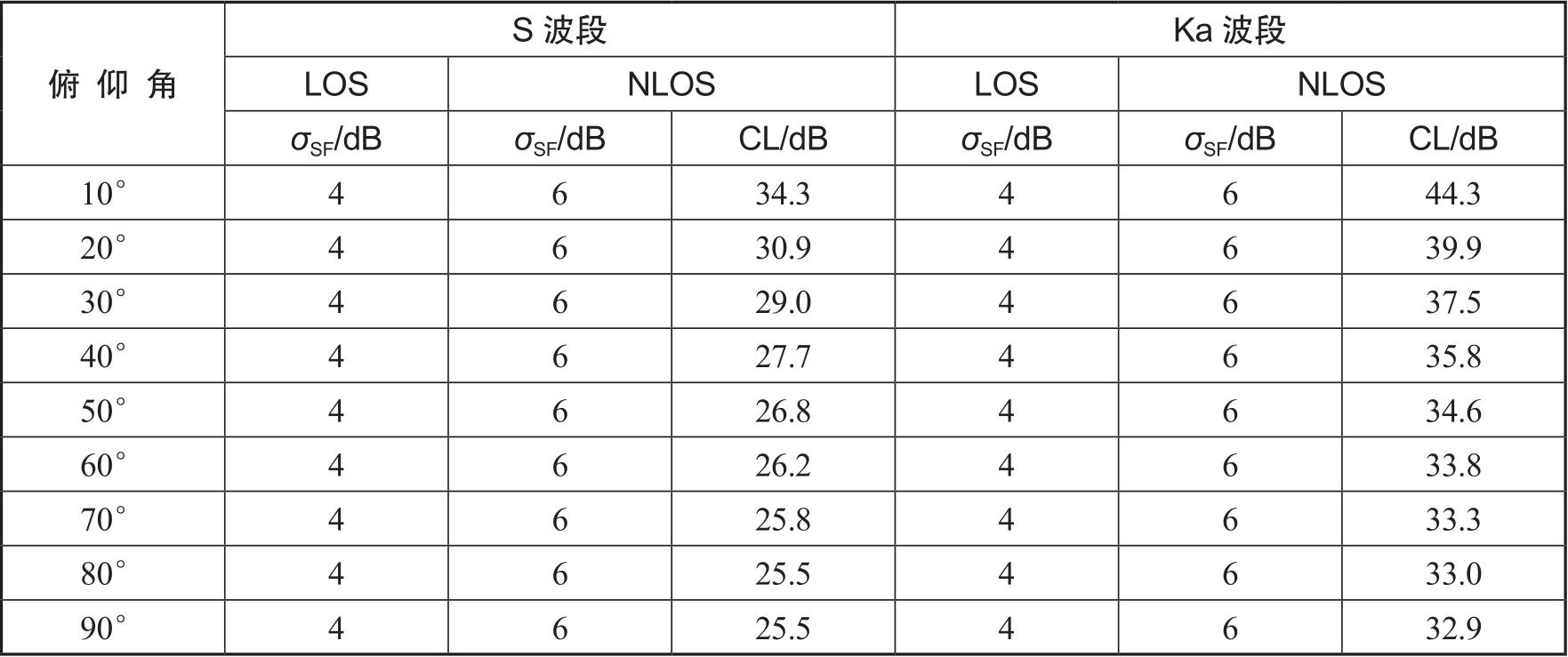
表3-8 郊区或乡村场景的阴影衰落( σ SF )和杂物路损(CL)
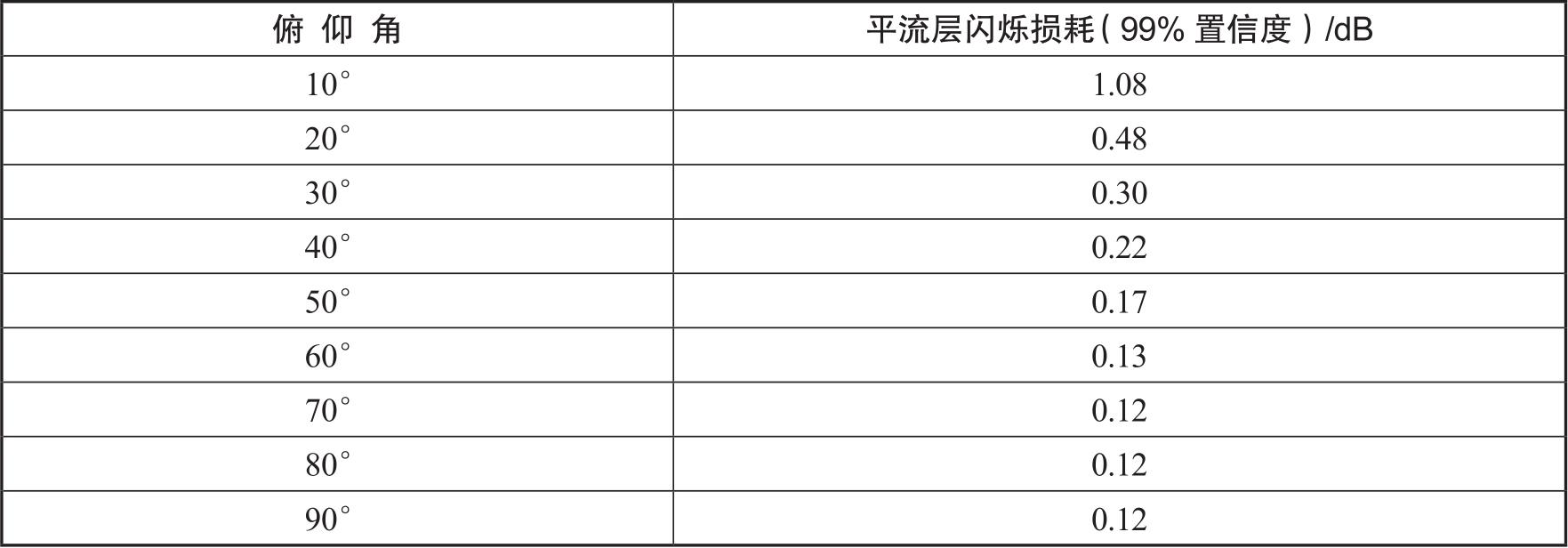
对于6 GHz以上的载频,温度、水汽比例和气压的变化造成空气折射系数的快速变化,形成卫星-地面信道的平流层闪烁损耗,其大小也与俯仰角大小有关,如表3-9所示。
表3-9 法国图卢兹地区20GHz卫星-地面信道的平流层闪烁损耗(99%置信度) [7]
考虑这些路损,为保证足够好的链路质量以支持较高的卫星-地面通信速率,对于密集城区,俯仰角一般需要在80°以上。对于城区,俯仰角需要在70°以上。而对于郊区或乡村,俯仰角可以低到30°。