




图2-23所示为履带拖拉机的运动学模型。拖拉机的状态用车身旋转中心在坐标系的位置及航向表示,令状态变量 p =( x yθ ) T ,其中 x 和 y 为履带拖拉机的位置, θ 为拖拉机前进方向与 X g 轴(北向)的夹角;对于速度可以自动调节的差速转向车辆,自动导航系统往往希望以 q =( v ω ) T 作为控制量,其中 v 和 ω 分别表示拖拉机的线速度和横摆角速度,在运动学模型中作为控制输入。
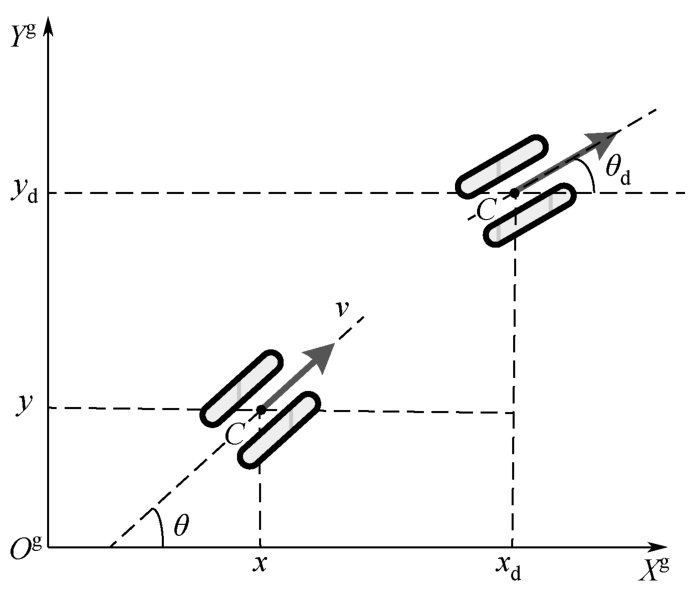
图2-23 履带拖拉机的运动学模型
履带型农用车辆的运动学方程为

从该运动学方程可知,履带拖拉机有3个自由度,而控制变量个数为2个,是典型的欠驱动系统,只能实现2个变量的主动跟踪,剩余的变量为随动或镇定状态。需要通过设计控制率 q =( v ω ) T 实现期望位置( x d y d )的跟踪,并实现夹角 θ 的随动。
式(2-99)也可写为

由上述分析可知,该运动学模型适用于所有以 q =( v ω ) T 作为控制量的农用车辆。
履带拖拉机速度与转向执行机构均采用液压泵控制,可以通过大扭矩舵机直接改造为电信号控制。改造后,履带拖拉机的差速转向系统控制框图如图2-24所示。
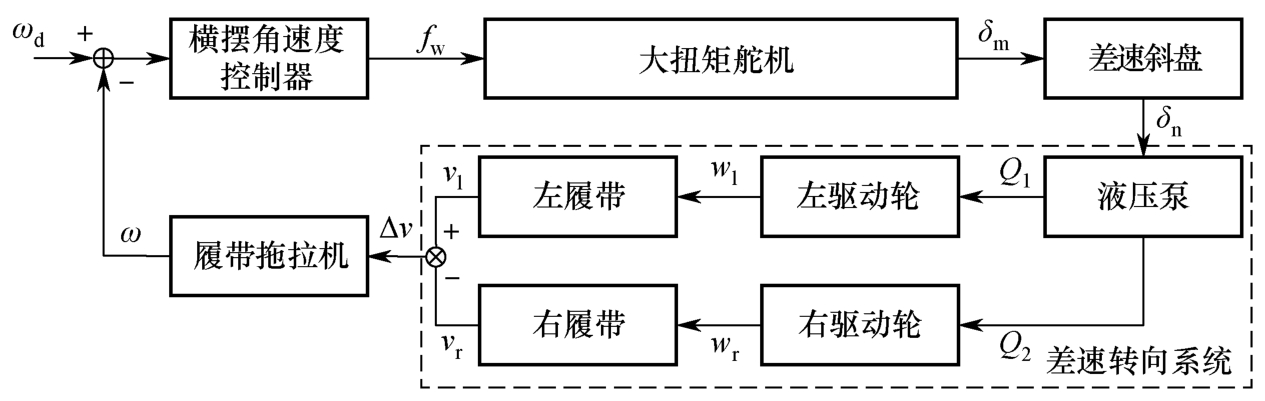
图2-24 履带拖拉机的差速转向系统控制框图
图2-24中 ω d 为期望横摆角速度, f w 为横摆角速度控制器输出的控制信号, δ m 为舵机角度, δ n 为连杆机构带动差速斜盘转过的角度, Q 1 和 Q 2 分别为差速液压泵供应给左、右履带驱动机构的流量值, w l 为左驱动轮转速, w r 为右驱动轮转速, v l 为左履带速度, v r 为右履带速度,Δ v 为两侧履带的速度差, ω 为履带拖拉机的横摆角速度。分析该系统各环节的数学模型如下:
(1)大扭矩舵机是转向系统的驱动装置,在理想情况下, δ m 与 f w 之间呈积分关系,其传递函数为

若考虑系统惯性,可将该传递函数表示为

式中, τ m 为时间常数, K m 为比例增益。
(2)大扭矩舵机和差速斜盘之间的连杆结构相当于一个比例环节,其比例系数为 K n 。
(3)设驱动轮半径为 r ,履带速度与驱动轮转速的关系为

设两侧履带的速度差为Δ v = v l -v r ,液压差速泵分配给两侧驱动轮的流量差为Δ Q = Q 1 -Q 2 ,由差速转向系统的结构可知, δ n 与Δ Q 成比例关系,Δ Q 与Δ v 成比例关系,因此,可将图2-24中的差速转向系统整体看作一个比例环节,其比例系数为 K v 。
(4)履带拖拉机的横摆角速度 ω 主要由两侧履带的速度差和履带间距决定,履带间距为 l ,横摆角速度 ω 可表示为

由上述分析可知

令

可得最终传递函数为

式中的 K a 和 τ m 可以通过系统辨识实验求出。
履带拖拉机的调速系统控制框图如图2-25所示。其中, v d 为期望车速, f v 为车辆线速度控制器输出的控制信号, δ m 为舵机角度, δ v 为调速斜盘转动的角度, Q n 为行走液压泵的输出流量, w n 为驱动轮转速, v 为履带拖拉机的实际行驶速度。
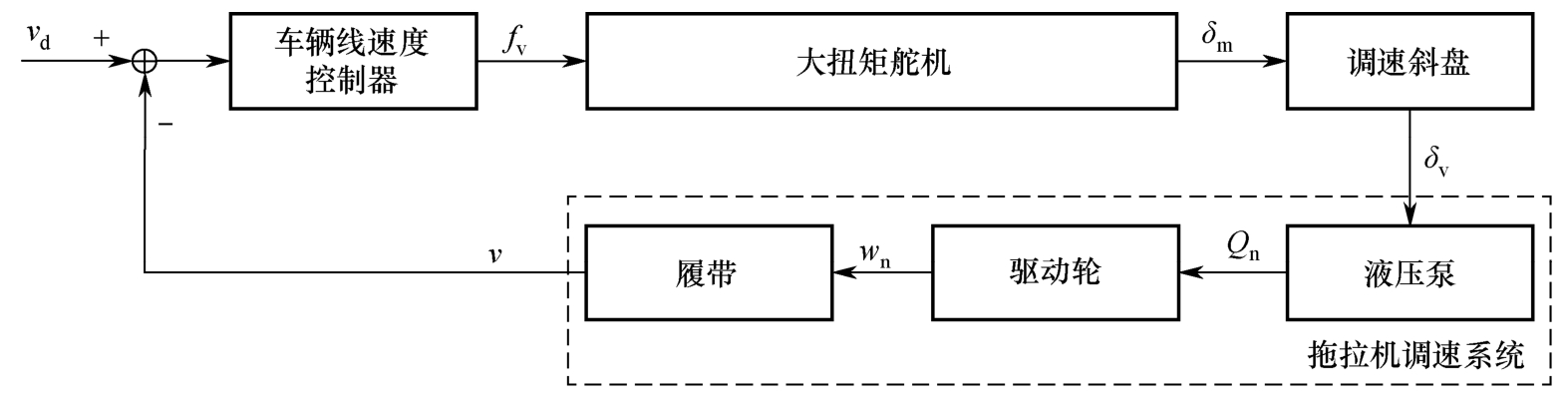
图2-25 履带拖拉机的调速系统控制框图
比较图2-24和图2-25可知,履带拖拉机的差速转向系统和调速系统改造后具有一定的相似性。图2-25中的拖拉机原调速系统可以看作比例环节,参考上文分析可得履带拖拉机调速系统的数学模型为

式中的 K b 和 τ n 可以通过系统辨识实验求出。
路径跟踪控制问题描述如图2-26所示。预设路径和农机状态在平面坐标系 X g -O g -Y g 下定义。( x c , y c )表示农机当前的位置, θ c 表示农机当前的航向,( x d , y d )表示期望的农机位置, θ d 表示期望的农机航向, d ( t )表示农机当前位置与期望位置的距离偏差, v 表示车辆当前速度, v d 表示期望的参考速度。农机的路径跟踪控制就是通过自动调节车辆的方向或速度,使其实际位姿与期望位姿趋向一致的过程。
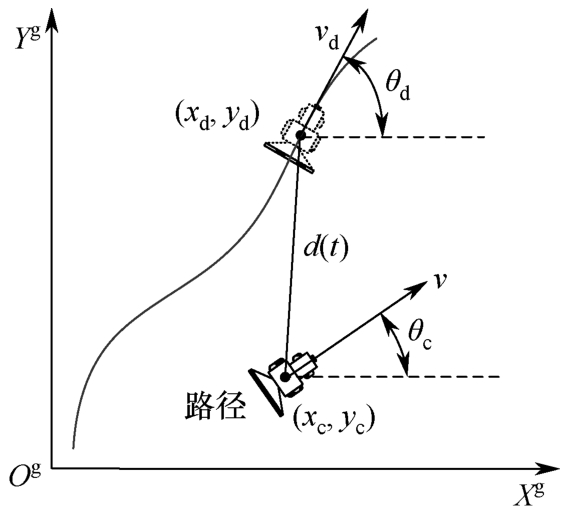
图2-26 路径跟踪控制问题描述
将农机当前的航向偏差定义为 θ e ,由图2-26可知
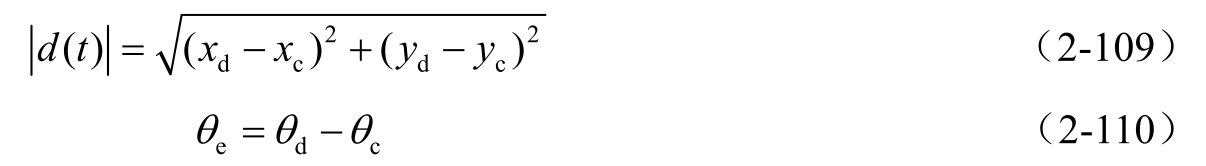
将农机的路径跟踪偏差定义为 e ( t ),有

本书将农机路径跟踪控制问题描述如下。
Q 1 :前向动态路径搜索,即期望参考速度 v d >0。
Q 2 :路径跟踪偏差衰减,即跟踪偏差 e ( t )→0。
Q 1 表示本书所述的农机自动导航系统只考虑前向行驶工况,不考虑倒车。考虑到农机导航作业过程中位置跟踪误差是需要被重点考虑的指标,因此,本书将 d ( t )作为路径跟踪精度的主要评价参数, Q 2 可放松为 d ( t )→0。综上,将 d ( t )离散化后的统计量作为路径跟踪性能评价参数:
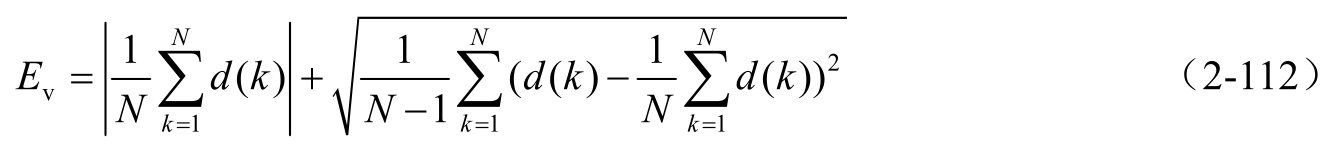
式中, E v 为路径跟踪性能评价参数, k =1,2,…, N 表示采样时刻, N 表示测试时长, d ( k )表示第 k 个时刻的农机位置偏差。式(2-112)由两部分组成,前半部分为偏差均值的绝对值,可以从整体上反映路径跟踪的误差趋势;后半部分为偏差标准差,可以反映农机路径跟踪控制的稳态效果。
对于导航过程中无法调速的农用车辆,实时动态寻优规划器有助于减小上线距离,提高上线点处的路径跟踪精度。但是,随着无级变速系统在农业机械上的广泛应用,通过设计合适的控制律对农机的线速度和横摆角速度进行联合控制,有助于进一步提高路径跟踪精度,减小上线距离,改善导航作业品质。
对于既可以调速也可以控制横摆角速度的农业车辆,本书依据其导航末端执行机构特征,构建由位置控制器和航向控制器组成的内外环串级路径跟踪控制系统,位置—航向双闭环路径跟踪控制系统结构如图2-27所示。其中,位置子系统滑模控制器为外环,输入量为当前车辆位置( x , y )和期望位置( x d , y d ),输出量为期望速度 v d ,外环同时产生中间指令信号 θ d 并传递给内环系统;航向子系统滑模控制器为内环,输入量为当前航向 θ 和期望航向 θ . d ,输出为期望横摆角速度 ω d 。采用基于干扰补偿控制器的离散滑模控制方法跟踪期望线速度和期望横摆角速度。
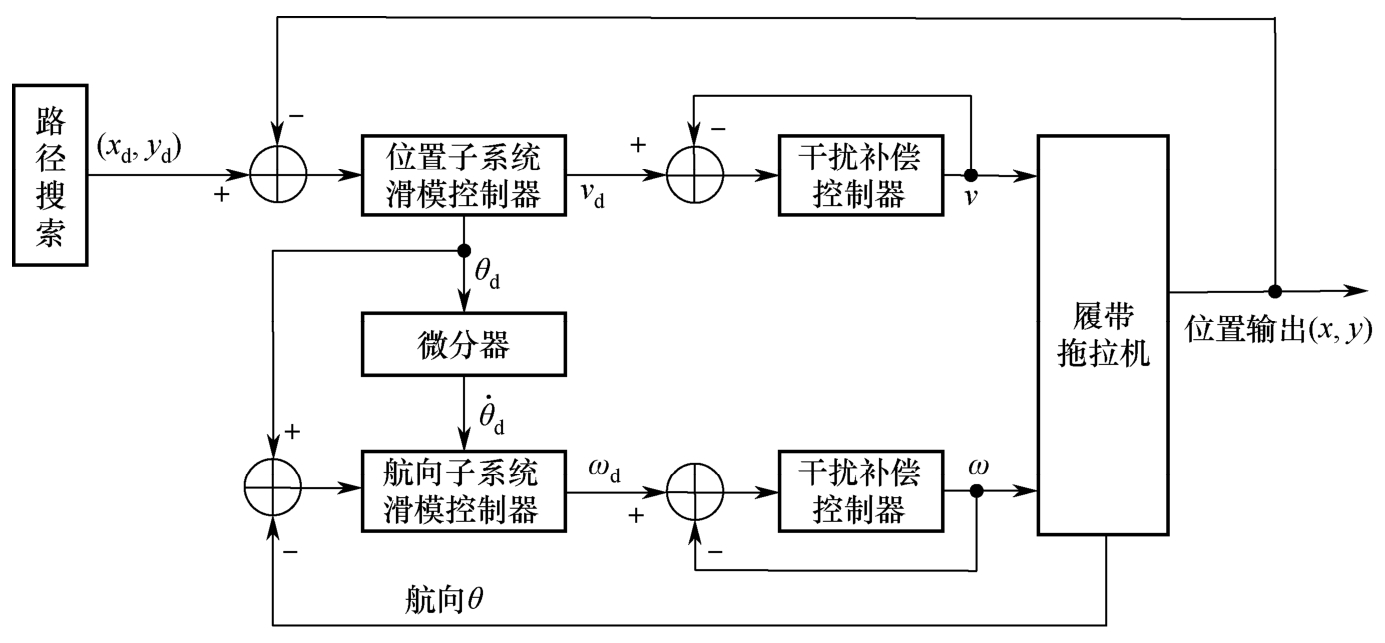
图2-27 位置—航向双闭环路径跟踪控制系统结构
为了实现稳定的内外环控制,工程上一般采用内环收敛速度大于外环收敛速度的方法,通过 θ 快速跟踪 θ d 来保证闭环系统的稳定性,但是该方法只是经验性方法,无法从理论上保证闭环系统稳定,为此,提出一种基于双曲正切函数的双闭环全局稳定串级滑模控制方法。
对于

其中, a , k >0。
当
x
→∞时,
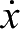 →0。
→0。
证明如下:
考虑函数
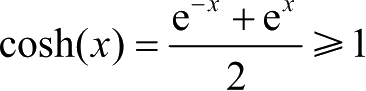 ,ln(cosh(
x
))≥0,且
x
=0时,ln(cosh(
x
))=0。为了证明当
t
→∞时,有
x
→0,定义李雅普诺夫函数为
,ln(cosh(
x
))≥0,且
x
=0时,ln(cosh(
x
))=0。为了证明当
t
→∞时,有
x
→0,定义李雅普诺夫函数为

则

由于
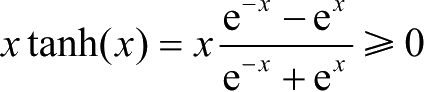 ,则
kx
tanh(
kx
)≥0,从而
V
.≤0;当且仅当
x
=0时,
V
=0。系统的收敛速度取决于
a
,
k
。
,则
kx
tanh(
kx
)≥0,从而
V
.≤0;当且仅当
x
=0时,
V
=0。系统的收敛速度取决于
a
,
k
。
由于
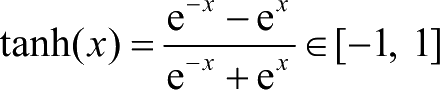 ,则
,则

如果针对模型式(2-113)的结构,并按式(2-25)设计控制率,便可实现控制输入的有界。
1.位置控制率设计
首先设计位置外环控制器。本书研究的履带拖拉机属于典型的可调速农业车辆,令 x e = x-x d , y e = y-y d ,则由履带拖拉机的运动学模型式(2-99)可知误差跟踪模型为

初步取控制指令 u 1 和 u 2 为

由式(2-117)和式(2-118)可知

令
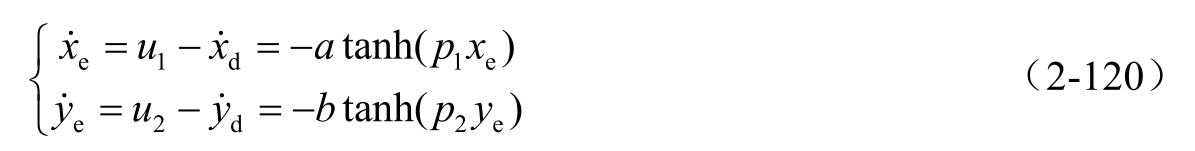
则由全局渐进稳定定理式(2-113)可知,当 t →∞时, x e →0, y e →0。
此时,由式(2-120)可得位置控制律为

其中, a >0, p 1 >0, b >0, p 2 >0。
由式(2-118)和式(2-121),可得位置外环输出的期望速度指令为

由式(2-118)可得
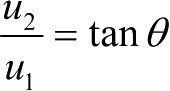 。由于本书所述的农机自动导航系统只考虑前向行驶工况,因此,
θ
的值域为(-π/2,π/2),则可得到满足理想轨迹跟踪的
θ
为
。由于本书所述的农机自动导航系统只考虑前向行驶工况,因此,
θ
的值域为(-π/2,π/2),则可得到满足理想轨迹跟踪的
θ
为

式(2-123)所求得的 θ 为位置控制律所要求的航向角,如果 θ 与 θ d 相等,则理想的轨迹控制律可实现,但实际 θ 与 θ d 不可能完全一致,尤其是控制的初始阶段,这会造成闭环跟踪系统的不稳定,为此,路径跟踪控制器需要跟踪的中间期望航向指令 θ d 为

2.航向控制率设计
通过设计航向内环控制器,实现 θ 跟踪位置控制率产生的 θ d 。
令 θ e = θ-θ d ,取滑模函数为 ς = θ e ,则

基于指数趋近律设计航向内环控制律为

式中, k 1 >0, η 1 >0。
于是
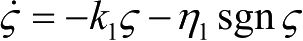 ,取
,取
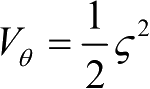 ,则
,则
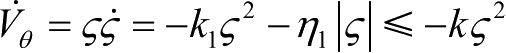 ,即
,即
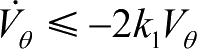 ,从而实现
θ
跟踪
θ
d
。
,从而实现
θ
跟踪
θ
d
。
在控制律式(2-126)中需要对位置外环产生的
θ
d
求导,为了工程实现方便,采用线性二阶微分器实现
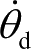 。
。
3.算法稳定性分析
假设存在理想的角度 θ d 满足轨迹跟踪控制,则模型可写为
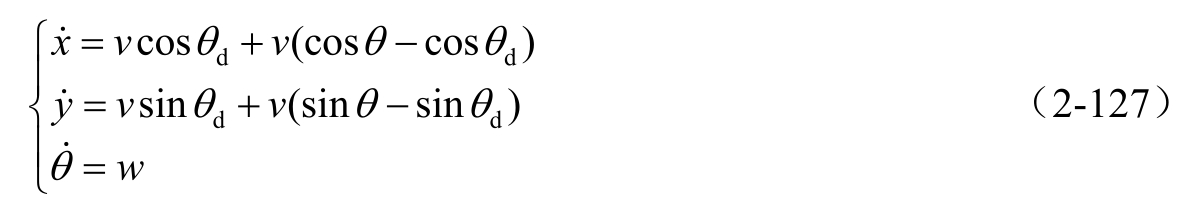
可见,如果 θ 与 θ d 不一致,必然会对位置闭环系统稳定性造成影响。如果考虑航向角度跟踪误差的影响,则按控制律式(2-126)进行设计,式(2-127)变为
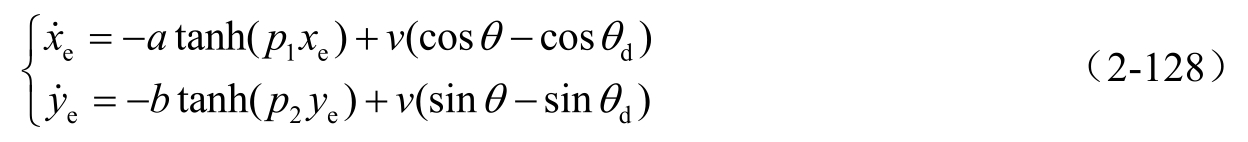
由于 u 1 和 u 2 有界,从而 v 有界,则闭环系统式(2-121)满足全局Lipschitz条件,对于任何初始状态, x e 和 y e 在任何有限时间内有界。
首先,针对闭环系统式(2-128)分析
x
e
的收敛性。考虑函数
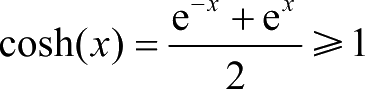 ,ln(cosh(
x
))≥0,且
x
=0时,ln(cosh(
x
))=0。为了证明当
t
→∞时,有
x
e
→0,定义李雅普诺夫函数为
,ln(cosh(
x
))≥0,且
x
=0时,ln(cosh(
x
))=0。为了证明当
t
→∞时,有
x
e
→0,定义李雅普诺夫函数为

式中, a >0, p 1 >0。
于是
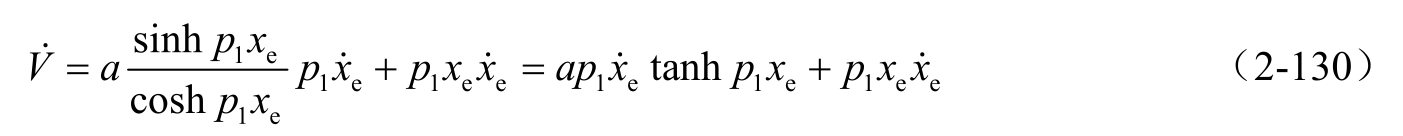
考虑
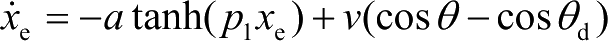 ,令
t
1
=
a
tanh(
p
1
x
e
),
t
2
=
v
(cos
θ
-cos
θ
d
),则
,令
t
1
=
a
tanh(
p
1
x
e
),
t
2
=
v
(cos
θ
-cos
θ
d
),则
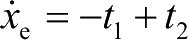 ,式(2-130)可写为
,式(2-130)可写为
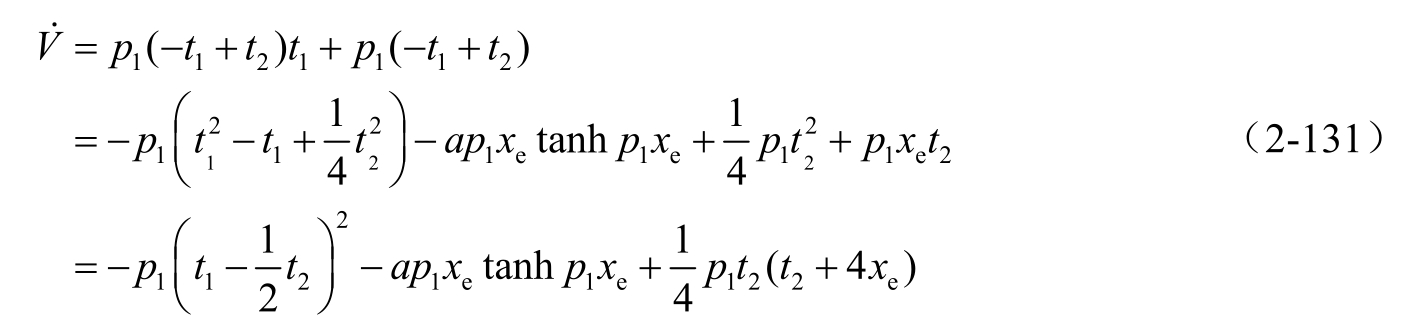
根据正弦函数的性质cos(
A
+
B
)-cos(
A-B
)=-2sin
A
sin
B
,取
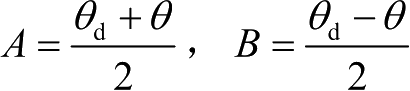 ,有
,有
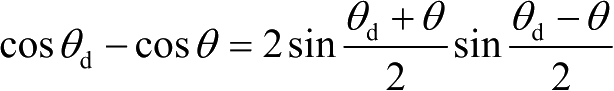 ,则
,则
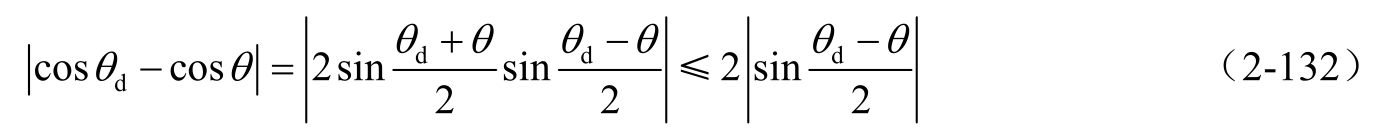
根据正弦函数的性质|sin
x
|≤|
x
[,有
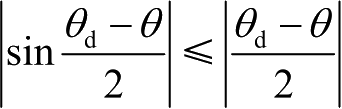 ,则可得
,则可得

由于 θ d -θ 指数收敛,则|cos θ -cos θ d |指数收敛,从而 t 2 = v (cos θ -cos θ d )指数收敛。由于 ap 1 x e tanh p 1 x e >0,所以
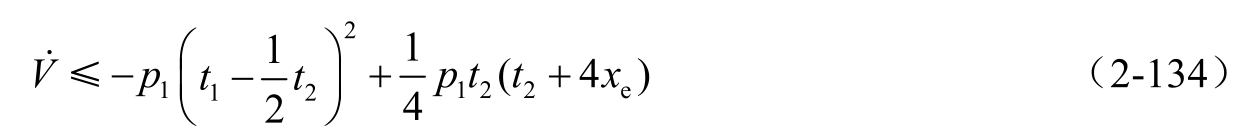
由于
t
2
指数收敛,对于任意
κ
1
>0,存在一个有限时间
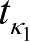 ,使得|
x
e
|≤
κ
1
成立。对于任意
κ
2
>0,存在一个有限时间
,使得|
x
e
|≤
κ
1
成立。对于任意
κ
2
>0,存在一个有限时间
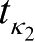 ,使得[
x
e
|≥
κ
2
成立,
,使得[
x
e
|≥
κ
2
成立,
 成立。因此,
x
e
在有限时间内收敛到半径为
κ
2
的紧集内。又由于当
t
→∞时,
t
1
→0,
θ-θ
d
→0,
t
2
→0且指数收敛,从而当
t
→∞时,
x
e
→0。由于|sin
θ
d
-sin
θ
|≤|
θ
d
-θ
|,则|sin
θ
d
-sin
θ
|指数收敛,有当
t
→∞时,
y
e
→0。
成立。因此,
x
e
在有限时间内收敛到半径为
κ
2
的紧集内。又由于当
t
→∞时,
t
1
→0,
θ-θ
d
→0,
t
2
→0且指数收敛,从而当
t
→∞时,
x
e
→0。由于|sin
θ
d
-sin
θ
|≤|
θ
d
-θ
|,则|sin
θ
d
-sin
θ
|指数收敛,有当
t
→∞时,
y
e
→0。
由以上分析可知,由于本算法考虑了内环航向跟踪误差对位置跟踪闭环系统稳定性的影响,因此,整个闭环系统是渐近稳定的。