




拖拉机转向前轮的状态测量结果是影响导航控制效果的直接因素。针对轮式拖拉机的前轮状态测量,目前主要有绝对角度测量法和角速率测量法。绝对角度测量法检测精度较高,但机械连接件多,标定工作复杂;角速率测量法一般选用惯性器件,安装简便,工作寿命长,但受振动影响较大,影响测量精度。在实际应用中,无论上述何种测量方法,其角度测量装置都是整个系统中最易被损坏的部件,例如,裸露在外的线缆很容易被农作物割坏,导致无法输出信号;机械连接机构在与农作物碰撞中易产生变形甚至损坏,导致角度测量值出现较大的误差。这些故障将直接影响转向系统的控制效果,严重时甚至影响自动导航系统的可靠性和安全性,因此,有必要针对前轮转角的容错预估方法开展研究。
下面以线性二自由度车辆模型为基础,研究拖拉机的转向特征,分析拖拉机运动过程中横摆角速度和侧偏加速度与前轮转角的关系。分析时,令拖拉机车体坐标系的原点与拖拉机的质心重合,并做如下假设:
(1)忽略空气动力作用;
(2)忽略地面切向作用力对拖拉机轮胎侧偏特性的影响;
(3)忽略拖拉机载荷变化导致的轮胎特性变化;
(4)忽略轮胎回正力矩的作用;
(5)拖拉机在二维平面内运动,忽略俯仰和横滚的影响;
(6)拖拉机的前进速度不变,只有横向运动与横摆两个自由度。
在上述假设条件下,拖拉机可简化为线性二自由度模型,如图2-14所示。
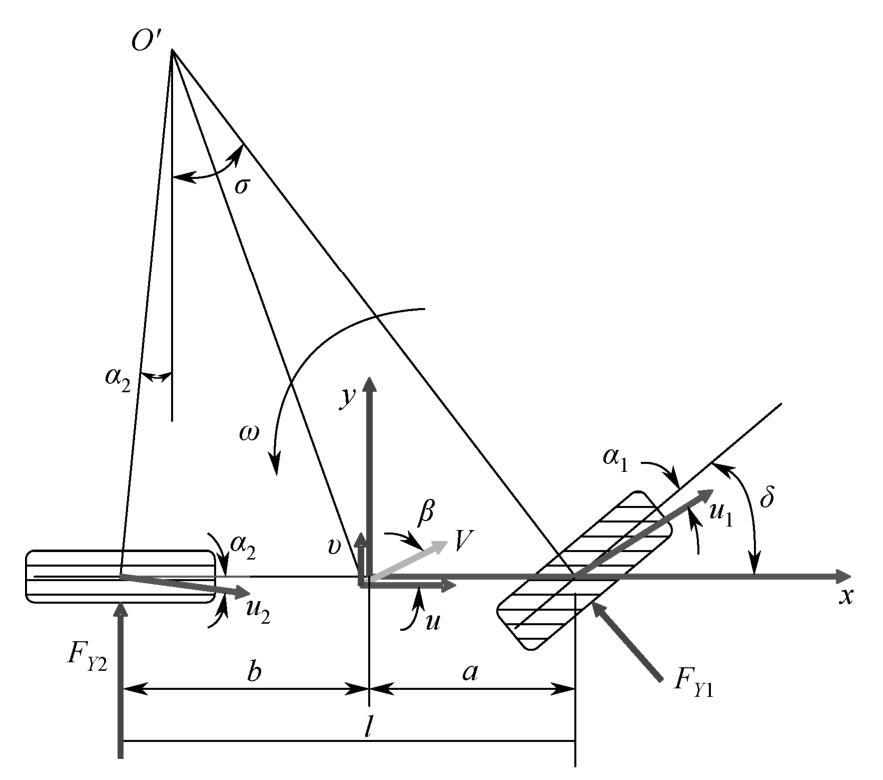
图2-14 线性二自由度拖拉机模型
图2-14中 l 为拖拉机轴距(m), a 为质心到前轴的距离(m), b 为质心到后轴的距离(m), V 为拖拉机的速度(m·s -1 ), u 为车辆质心处的纵向速度(m·s -1 ), v 为车辆质心处的横向速度(m·s -1 ), β 为车辆质心处侧偏角(rad), ω 为拖拉机的横摆角速度(rad·s -1 ), δ 为前轮转角(rad), F Y 1 和 F Y 2 分别对应地面对前、后轮的侧偏力(N), α 1 和 α 2 分别对应前后轮的侧偏角(rad), u 1 和 u 2 是拖拉机前后轴中点的速度(m·s -1 ), σ 是 u 1 与 x 轴的夹角(rad)。
从图2-14中可以看出,二自由度拖拉机沿 y 轴的外力与围绕质心的力矩的合力为

侧偏角与侧偏力的关系为

式中, k 1 和 k 2 分别为前、后轮的侧偏刚度。因为 δ 角较小,所以cos δ ≈1,此时式(2-39)可以进一步写为

质心侧偏角与速度分量的关系为

σ 的计算式为

前后轮的侧偏角 α 1 和 α 2 的计算式为
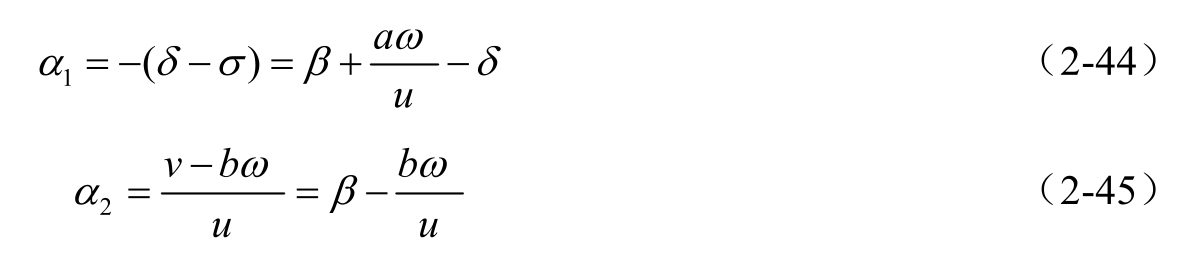
由此,外力、外力矩和拖拉机运动参数之间的关系可以表示为
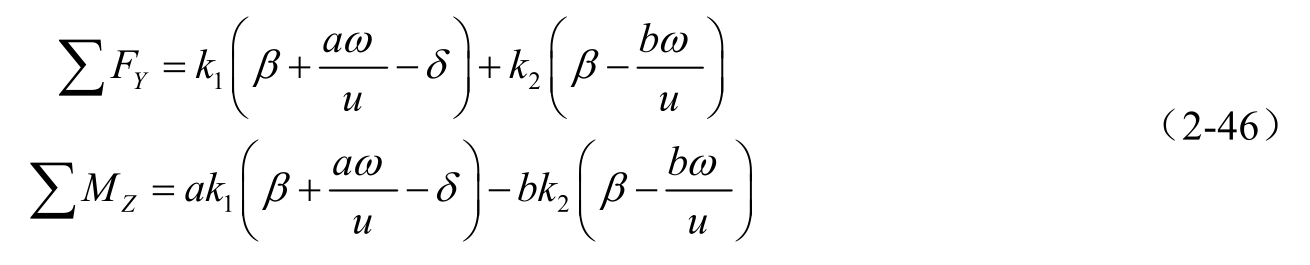
所以,二自由度拖拉机的运动微分方程式为
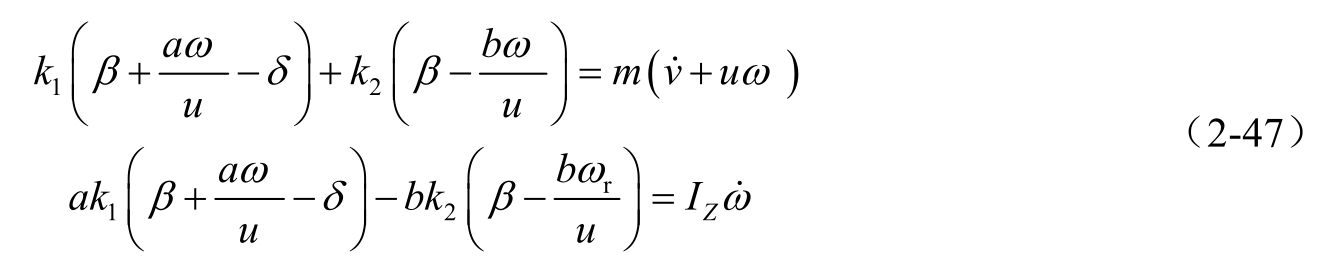
式中, I Z 为拖拉机绕 z 轴的惯性矩(kg·m²),进一步整理得
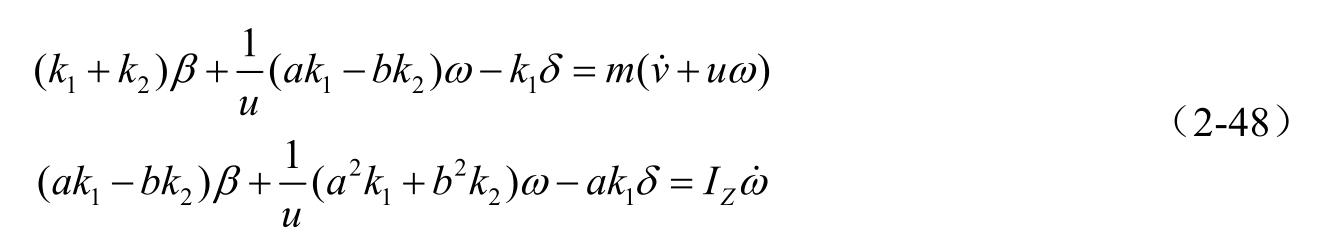
当拖拉机以恒定速度作业时,在前轮转角阶跃输入作用下的稳态响应为匀速圆周运动。此时,
 ,代入运动微分方程(2-48)可以求得
,代入运动微分方程(2-48)可以求得
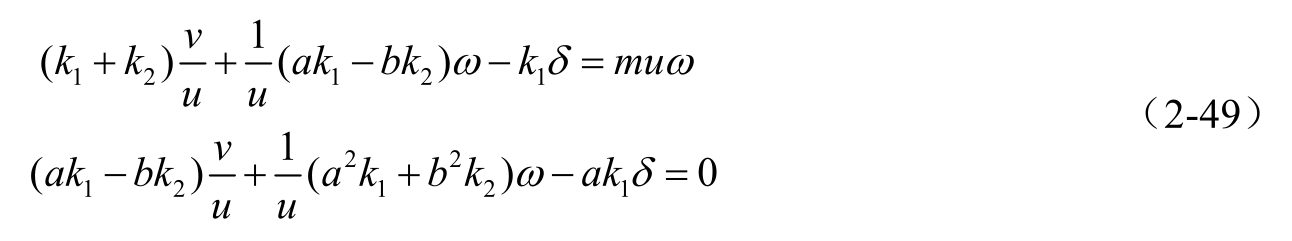
由式(2-49)可求得稳态时横摆角速度的增益表达式为

其中

于是,可求得拖拉机前轮转角与横摆角速度的关系为

由拖拉机前轮转角与侧向加速度 a y 在稳态时的关系可求得

1.基于卡尔曼(Kalman)滤波器的前轮转角传感器性能评估
轮式拖拉机自动转向控制系统的离散状态方程为

式中,
k
为离散时间;
i
(
k
)为系统在时刻
k
的控制量;状态变量
x
=(
x
1
,
x
2
)
T
,其中
x
1
=
δ
,
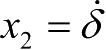 ;
W
(
k
)为过程噪声。
;
W
(
k
)为过程噪声。
基于横摆角速度 ω 和侧向加速度 a y 可以建立两个卡尔曼滤波器观测方程。由式(2-52)得横摆角速度的观测方程为
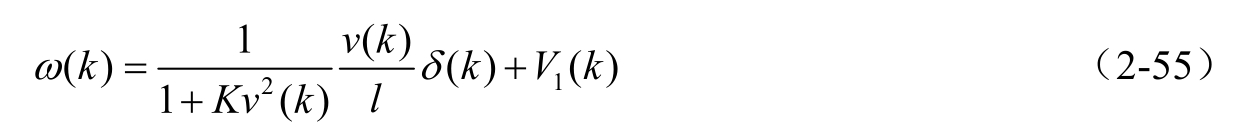
式中, V 1 ( k )为横摆角速度观测噪声,此时观测变量为 ω ( k )。
由式(2-53)可以求得侧向加速度的观测方程为
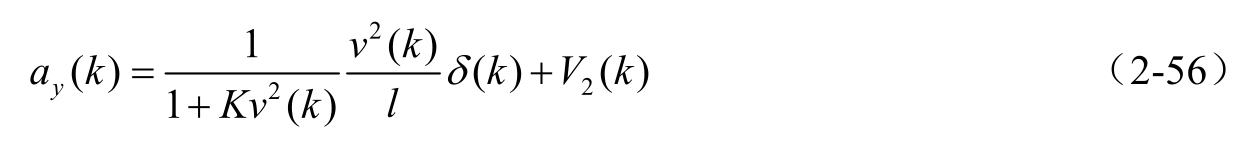
式中, V 2 ( k )为侧向加速度观测噪声,此时观测变量为 a y ( k )。
在工程实践中,传感器测量得到的原始数据中往往夹杂着干扰信号,常用的滤波器为卡尔曼滤波器,它可以有效降低噪声对真实信号的影响,提高系统对实际状态的估计精度,在国防、军事、跟踪等领域得到了广泛应用。
将拖拉机自动转向系统进一步用如下状态空间模型描述:
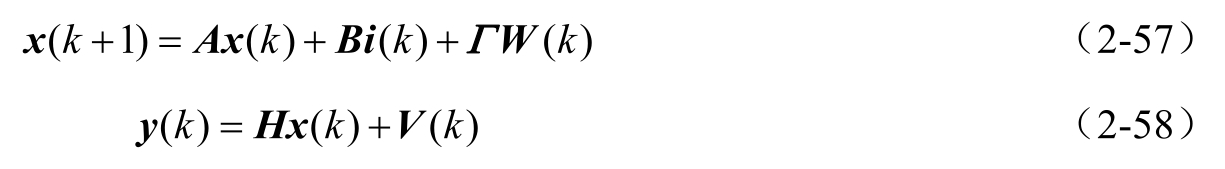
式中,

观测矩阵 H 的表达式为
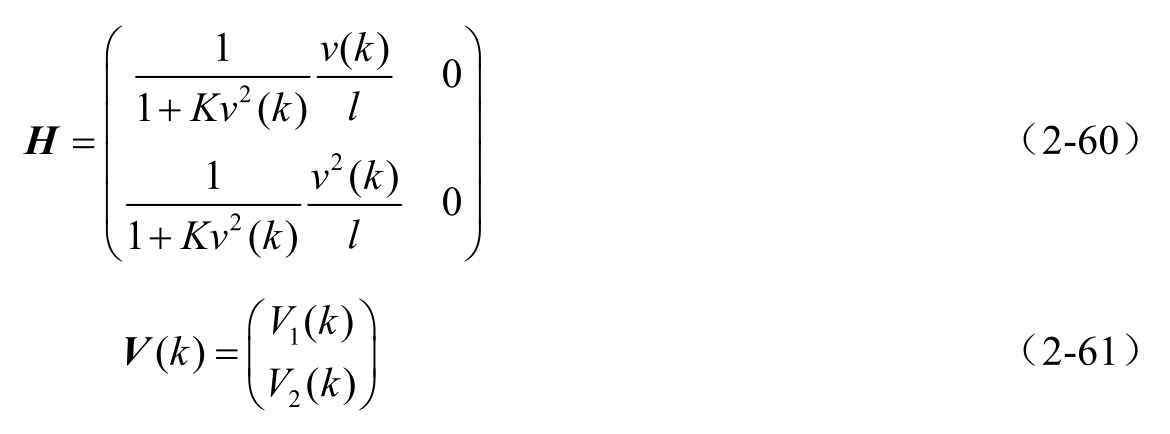
称 A 为状态转移矩阵, B 为控制矩阵, Γ 为噪声驱动矩阵。
假设状态空间中的参数满足如下条件:
(1) W ( k )和 V ( k )是均值为0的不相关白噪声, W ( k )的方差阵为 Q , V ( k )的方差阵为 R ; E [ W ( k )]=0, E [ V ( k )]=0, E [ W ( k ) W T ( j )]= Q η kj , E [ V ( k ) V T ( j )]= R η kj ; W ( k )和 V ( k )互不相关,因此,有 E [ W ( k ) V T ( j )]=0,∀ k , j ,其中 η kk =1, η kj =0,∀表示“任意”。
(2)初始状态 x (0)不相关于 W ( k )和 V ( k ),且有
E [ x (0)]= μ 0 , E [( x (0) -μ 0 )( x (0) -μ 0 ) T ]= P 0
在以上假设均满足的条件下,式(2-57)和式(2-58)的卡尔曼滤波器可描述如下。
状态预测方程:

状态更新方程:
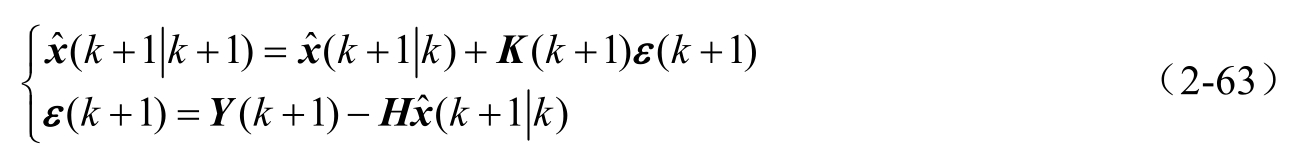
增益矩阵更新:
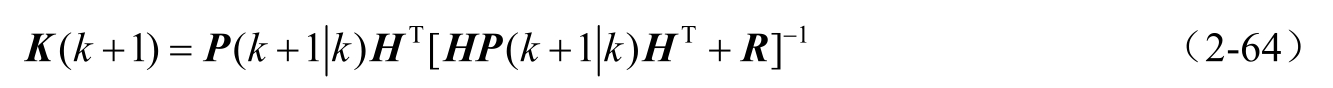
一步预测协方差阵:
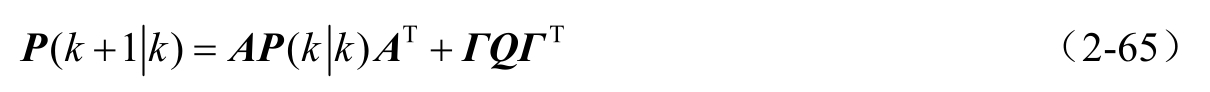
协方差阵更新:
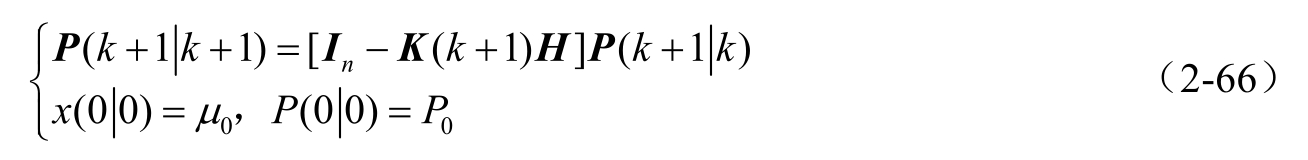
通过递推卡尔曼滤波器方程可以得到拖拉机前轮转角在
k
时刻基于横摆角速度的估计值
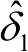 和基于侧向加速度的估计值
和基于侧向加速度的估计值
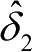 。设基于角度编码器的测量值为
δ
,通过提取残差特征参数,设定诊断规则可以判断前轮转角传感器的故障情况,进而建立前轮角度容错输出规则。
。设基于角度编码器的测量值为
δ
,通过提取残差特征参数,设定诊断规则可以判断前轮转角传感器的故障情况,进而建立前轮角度容错输出规则。
由
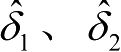 和
δ
可以得到三组残差特征方程为
和
δ
可以得到三组残差特征方程为

式中,
r
i
(
i
=1,2,3)为转角残差,设其对应的阈值为
z
i
(
i
=1,2,3),实际应用时该阈值依据
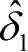 和
和
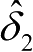 的预估精度确定。取故障特征矢量为
S
i
(
i
=1,2,3),
S
i
与转角残差及对应阈值的关系为
的预估精度确定。取故障特征矢量为
S
i
(
i
=1,2,3),
S
i
与转角残差及对应阈值的关系为

式(2-68)中的矢量 S i 反映了传感器的故障信息:当 S i =0时,表示相应的两个传感器均正常,反之,表示其中有一个出现了故障。考虑到两类传感器同时发生故障的概率很小,所以,要么两个惯性器件之一发生故障,要么测量前轮转角的角度编码器发生故障。角度编码器工作状态 F s 的判断逻辑为
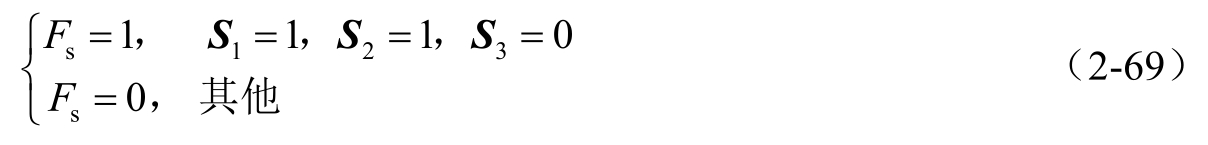
式中,1表示角度编码器出现故障;0表示正常。
综上,基于卡尔曼滤波器的前轮转角传感器故障诊断算法流程如图2-15所示。
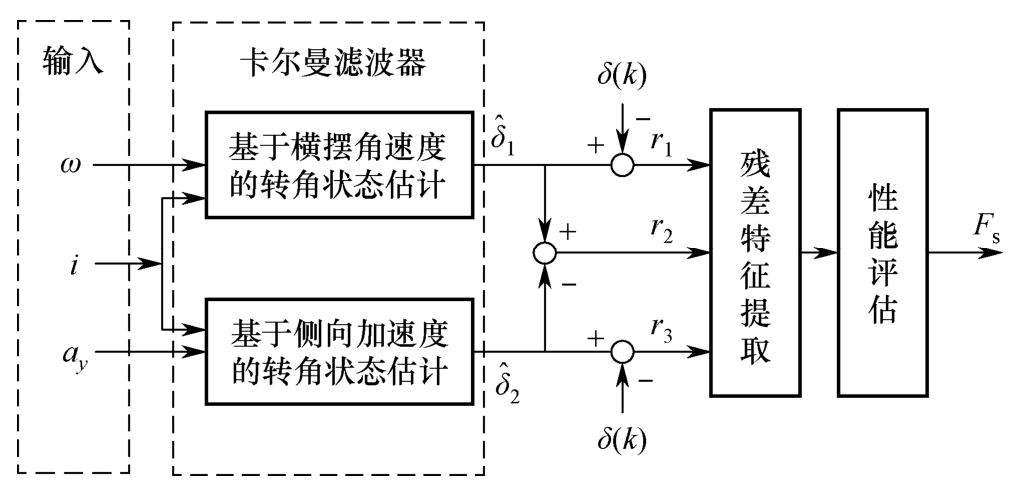
图2-15 基于卡尔曼滤波器的前轮转角传感器故障诊断算法流程
图2-15中,
ω
为横摆角速度,
i
为控制输出,
a
y
为侧向加速度,
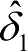 为基于横摆角速度的估计值,
为基于横摆角速度的估计值,
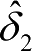 为基于侧向加速度的估计值,
δ
为前轮角度传感器的测量值,
r
i
(
i
=1,2,3)为转角残差,
F
s
为前轮角度传感器工作状态。
为基于侧向加速度的估计值,
δ
为前轮角度传感器的测量值,
r
i
(
i
=1,2,3)为转角残差,
F
s
为前轮角度传感器工作状态。
2.基于混合卡尔曼滤波器的前轮转角数据融合算法
基于卡尔曼滤波器的前轮角度性能评估方法执行效率较高,用来判断前轮转角传感器是否发生故障是合适的。但是,转向控制模型的不确定性和传感器干扰信号统计特性不完全已知,对卡尔曼滤波算法有较大的影响。当故障发生时,直接利用
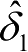 或
或
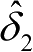 代替
δ
可以起到一定的作用,但是估计精度较低,会对导航控制精度产生较大的影响,因此,有必要针对控制模型不准确和不确定噪声情况进一步深入研究,以提高前轮转角的预估精度。
代替
δ
可以起到一定的作用,但是估计精度较低,会对导航控制精度产生较大的影响,因此,有必要针对控制模型不准确和不确定噪声情况进一步深入研究,以提高前轮转角的预估精度。
结合稳健加权观测融合卡尔曼滤波器,研究一种适用于农机导航领域使用的混合卡尔曼滤波器结构,对侧偏加速度传感器、横摆角速度传感器及前轮转角传感器的数据进行信息融合,在保证执行效率的同时进一步提高转角估计精度。
考虑带有不确定模型参数和噪声统计特性不完全已知的线性离散系统
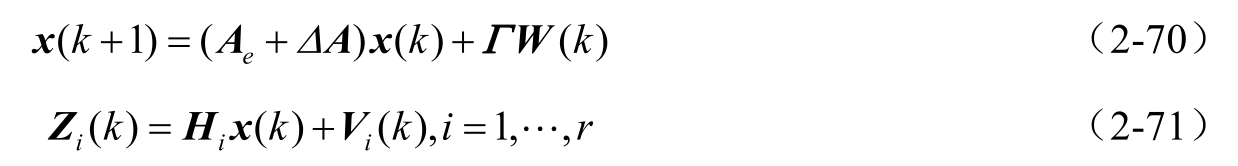
式中,
k
≥0表示离散时刻,
x
(
k
)∈
R
n
为被控对象在时刻
k
的状态,
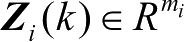 表示第
i
个子系统的观测,
W
(
k
)∈
R
r
为输入噪声,
表示第
i
个子系统的观测,
W
(
k
)∈
R
r
为输入噪声,
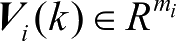 为第
i
个子测量系统的观测噪声。
Δ
A
为不确定模型参数,
A
e
、
Γ
和
H
i
是已知适当维数常阵,
A
=
A
e
+
Δ
A
为真实状态转移矩阵,
r
为测量传感器的个数。
为第
i
个子测量系统的观测噪声。
Δ
A
为不确定模型参数,
A
e
、
Γ
和
H
i
是已知适当维数常阵,
A
=
A
e
+
Δ
A
为真实状态转移矩阵,
r
为测量传感器的个数。
做如下假设:
(1)
W
(
k
)
∈R
r
和
V
(
k
)是互不相关的白噪声,它们的均值都为0;
W
(
k
)的真实方差为
 ,
V
(
k
)的真实方差为
,
V
(
k
)的真实方差为
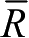 ,两者均是不确定的,并且满足
,两者均是不确定的,并且满足

式中,
Q
和
R
i
分别为
 和
和
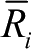 的保守上界。
的保守上界。
(2)真实状态转移矩阵 A 是稳定的。
(3)融合系统和子系统是完全可控、可观的。
第二个假设条件可以保障状态 x ( k )是一个方差有界、均值为零的平稳随机过程,不确定模型参数 Δ Ax ( k )可以近似看作白噪声,可以被虚拟噪声补偿,该虚拟噪声带有保守上界方差,且均值为0。
将带保守上界方差 Δ ξ 的虚拟噪声 ξ ( k )引入,用来补偿式(2-70)中的不确定模型参数 Δ Ax ( k ),则式(2-70)可以转换为带已知模型参数和保守噪声方差上界 Q 、 R i 和 Δ ξ 的保守系统
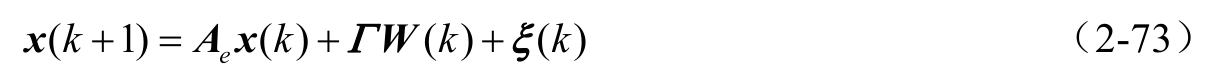
考虑集中型融合观测方程

其中,
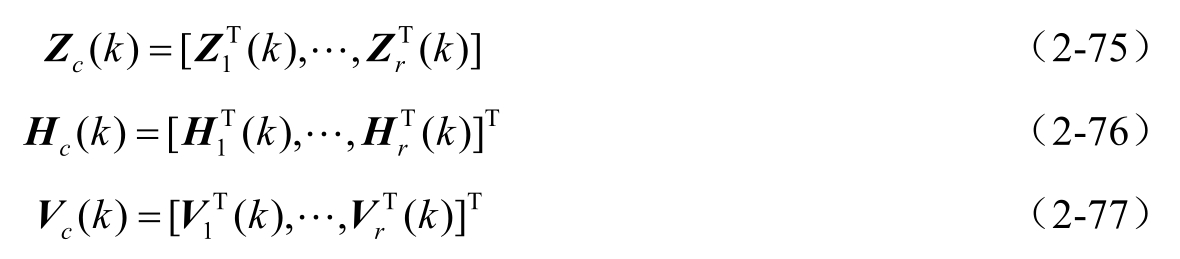
且 V c ( k )具有保守的观测方差阵

假设 H c ( k )列满秩,使用加权最小二乘法可将式(2-74)转化为

其中, Z M ( k )为保守的加权融合观测, V M ( k )为融合的观测白噪声,且有
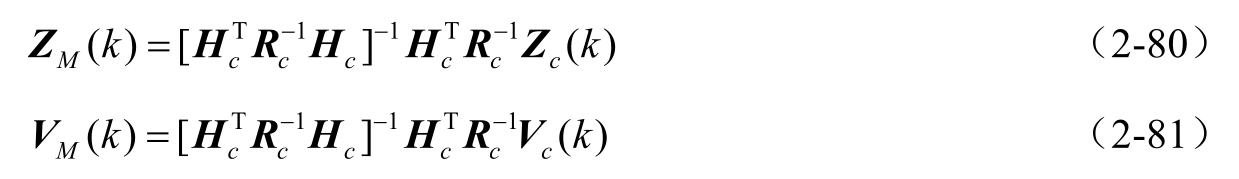
根据式(2-81),可知 V M ( k )具有保守的观测方差阵

对带保守上界 Q 、 R i 和 Δ ξ 的最坏情形系统式(2-73)和式(2-79),由极大极小稳健估值理论可知,有保守的最优加权观测融合稳态卡尔曼滤波器
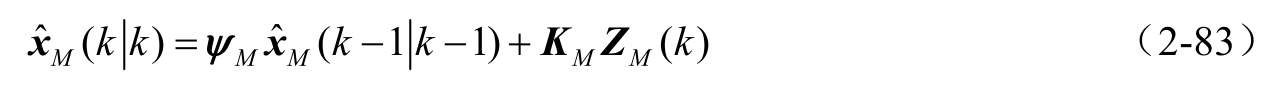
其中, ψ M 为稳定阵,表达式为

K M 的表达式为

式中, Σ M 满足稳态Riccati方程
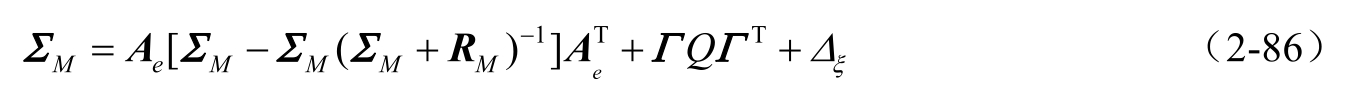
根据式(2-73)、式(2-80)和式(2-81),能够求出保守的滤波误差
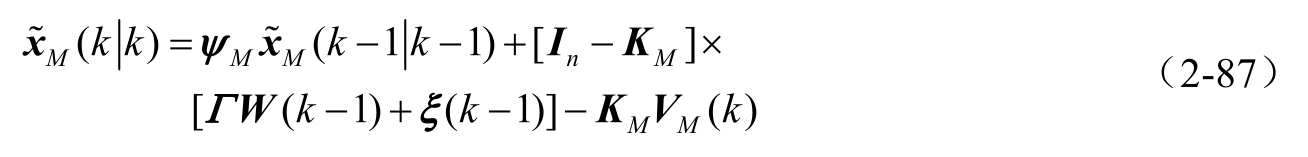
可以看出保守的滤波误差方差符合李雅普诺夫方程
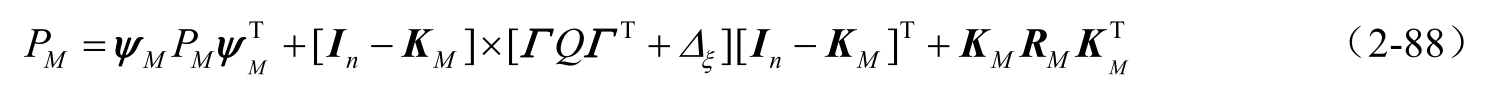
将
Q
和
R
i
替换为
 和
和
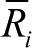 ,则式(2-83)就称作加权观测融合卡尔曼滤波器。
,则式(2-83)就称作加权观测融合卡尔曼滤波器。
为了求取实际的滤波误差,将其描述为

式中,
x
(
k
)为式(2-70)的真实状态,
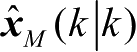 为式(2-83)给出的滤波输出值,则由式(2-70)减去式(2-83)可得实际滤波误差为
为式(2-83)给出的滤波输出值,则由式(2-70)减去式(2-83)可得实际滤波误差为
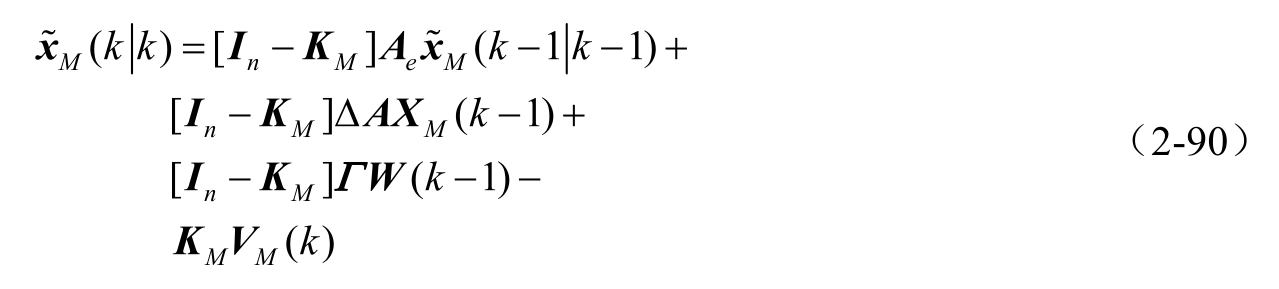
结合自动转向控制系统的状态方程和观测方程,以及稳健加权观测融合卡尔曼滤波器,可以很容易求得对不确定干扰稳健的预估角度值。此时,在上述理论研究基础上可将图2-15所示的故障诊断算法进一步改进为一种混合卡尔曼滤波器结构,如图2-16所示。图2-16中 δ out 为混合卡尔曼滤波器输出。
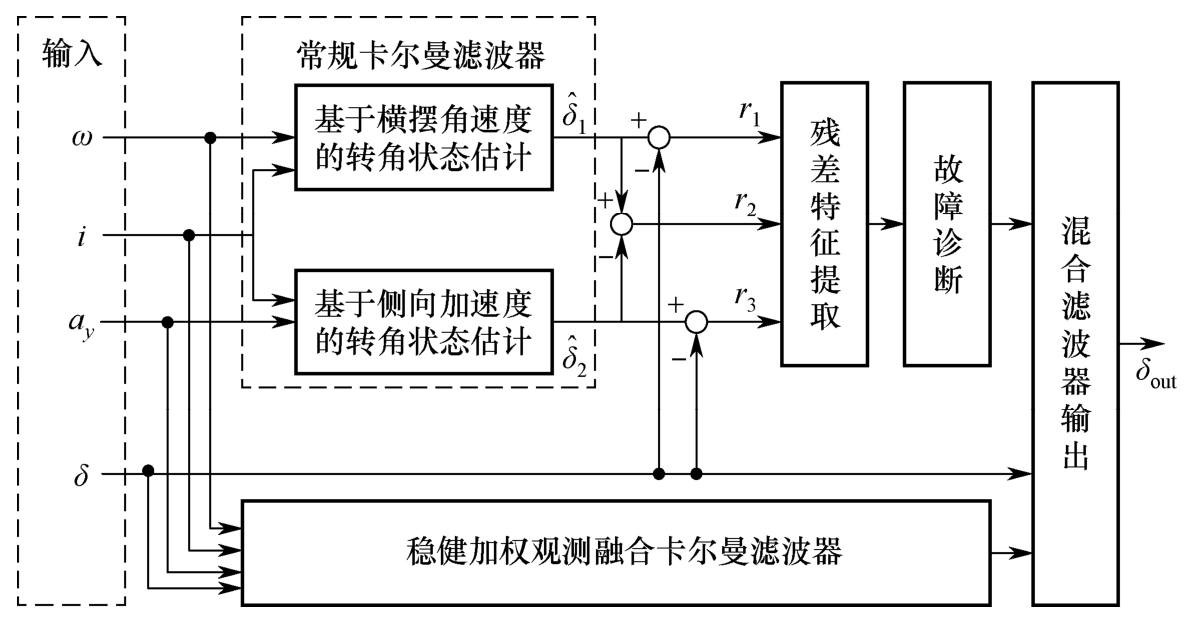
图2-16 基于混合卡尔曼滤波器的前轮转角传感器容错预估算法结构
图2-16采用分布式融合结构处理侧向加速度、横摆角速度和前轮转角编码器3个传感器的数据,采用常规卡尔曼滤波器对前轮转角传感器进行故障诊断。无故障发生时,主要采用前轮角度编码器测量值进行转向控制;当故障发生时,立即切换到多传感器信息融合输出,兼顾了传感器数据融合测量系统的实时性和测量精度。
拖拉机前轮转角多传感器信息融合测量试验在中国农机院北京农机试验站进行。由于试验场地限制,将车速控制在6km/h左右,试验现场如图2-17所示。
1.基于常规卡尔曼滤波器的前轮转角预估试验
在车辆行驶过程中,首先控制转向前轮从0°转动至20°,保持一段时间后控制前轮转动至-20°,通过测试过程中记录的试验数据验证基于常规卡尔曼滤波器的前轮转角预估算法的准确性。试验结果如图2-18和图2-19所示。

图2-17 拖拉机前轮转角多传感器容错预估试验现场
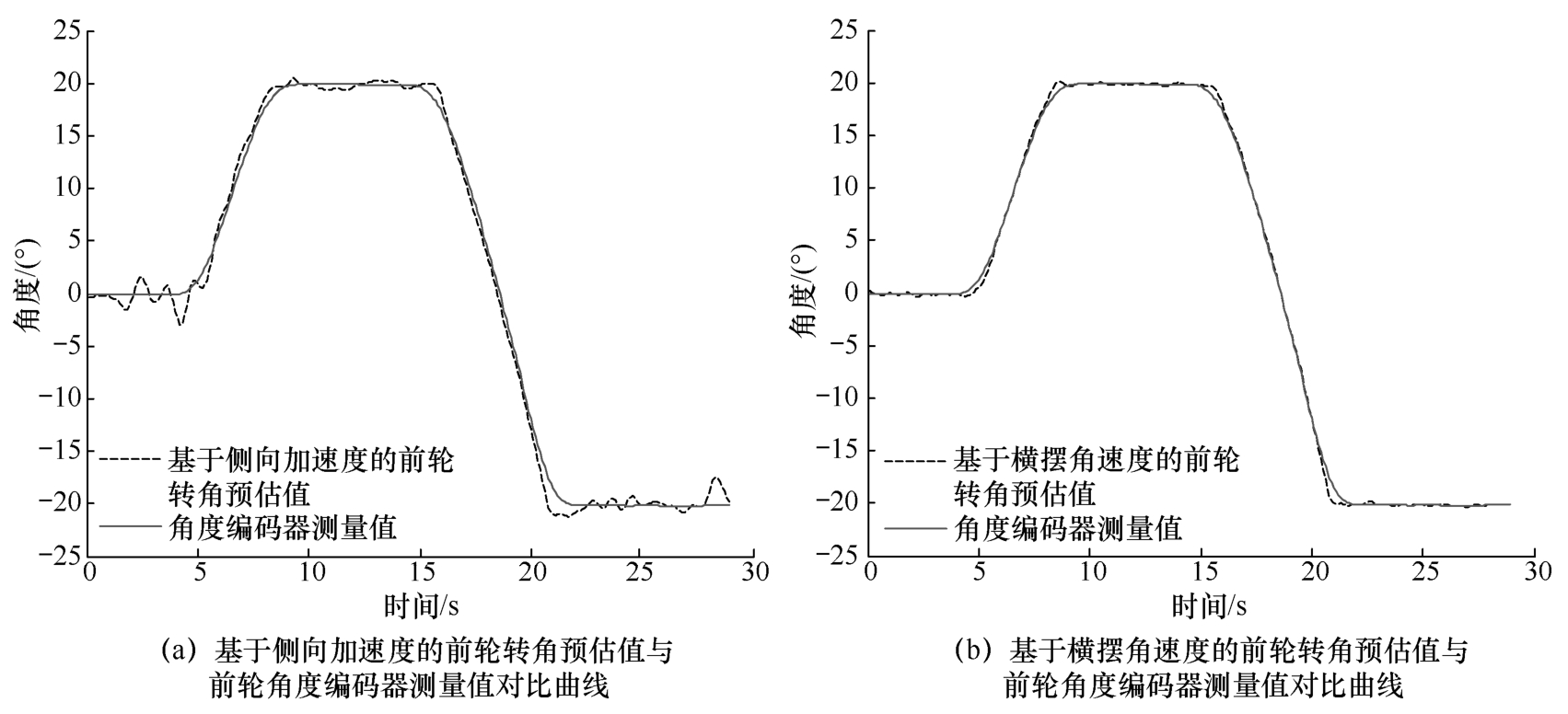
图2-18 基于侧向加速度和横摆角速度的前轮转角预估值
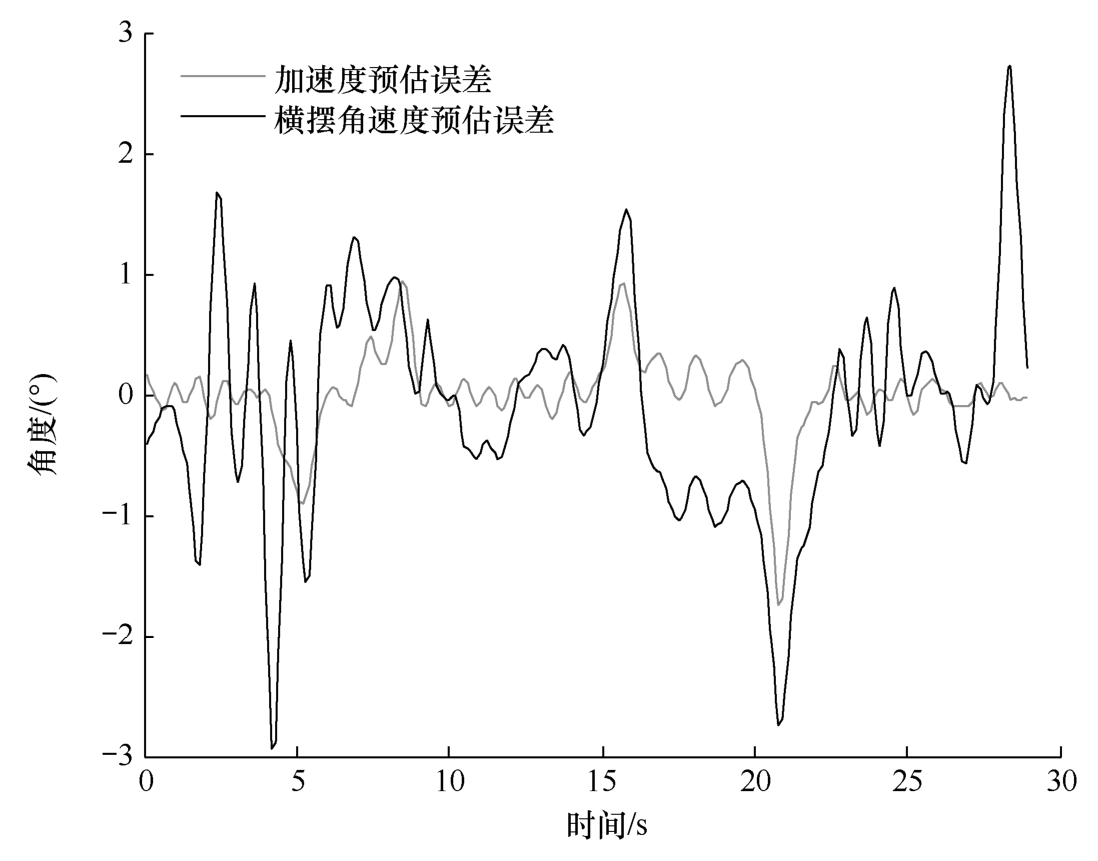
图2-19 基于侧向加速度和横摆角速度的前轮转角预估误差对比曲线
图2-18(a)所示为基于侧向加速度的前轮转角预估值
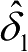 与前轮角度编码器测量值
δ
的对比曲线,图2-18(b)所示为基于横摆角速度的前轮转角预估值
与前轮角度编码器测量值
δ
的对比曲线,图2-18(b)所示为基于横摆角速度的前轮转角预估值
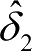 与前轮角度编码器测量值
δ
的对比曲线,从图中可以看到
与前轮角度编码器测量值
δ
的对比曲线,从图中可以看到
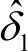 和
和
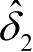 均可以较好地估计前轮转角数值,且无明显的滞后性。
均可以较好地估计前轮转角数值,且无明显的滞后性。
图2-19所示为基于侧向加速度和横摆角速度的前轮转角预估误差对比曲线。由数据统计结果可知:与编码器测量的角度值相比,基于侧向加速度的转角估计值最大误差为2.94°,均方根误差为0.81°;基于横摆角速度的转角估计值最大误差为1.73°,均方根误差为0.14°。前者数值波动相对较大,这是由于试验过程中加速度计受振动影响较大导致的。
误差分析:
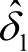 和
和
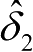 的预估误差较大,主要原因有两方面,一方面,测量过程中使用的RTK-GNSS、姿态传感器和前轮角度传感器均存在一定的偏差,这会给卡尔曼滤波算法带来预估误差;另一方面,车辆转向模型建立得不够准确,而且加速度计和角速度计的干扰信号统计特性不完全已知对常规卡尔曼滤波算法有较大的影响,导致了较大的预估误差。由统计数据可以看出,
的预估误差较大,主要原因有两方面,一方面,测量过程中使用的RTK-GNSS、姿态传感器和前轮角度传感器均存在一定的偏差,这会给卡尔曼滤波算法带来预估误差;另一方面,车辆转向模型建立得不够准确,而且加速度计和角速度计的干扰信号统计特性不完全已知对常规卡尔曼滤波算法有较大的影响,导致了较大的预估误差。由统计数据可以看出,
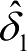 和
和
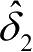 在高精度作业需求条件下仅可用于故障预警,无法完全代替编码器工作。
在高精度作业需求条件下仅可用于故障预警,无法完全代替编码器工作。
2.基于混合卡尔曼滤波器的前轮转角信息融合试验
控制拖拉机转向前轮从-10°向10°连续转动,保持一段时间后控制前轮转动至0°。当角度编码器测量值第一次到达0°附近时,人工对角度编码器施加-5°干扰,通过记录的试验数据验证基于混合卡尔曼滤波器的前轮转角信息融合方法的可行性和准确性。
试验结果如图2-20所示。由图2-20(a)可知,当编码器未施加错误信号时,算法输出的角度为编码器测量值,当编码器测量值施加干扰信号后,算法立刻检测到故障信息并切换为基于混合卡尔曼滤波器的容错输出。图2-20(b)所示为基于混合卡尔曼滤波器的前轮转角预估误差曲线。由数据统计结果可知,与编码器测量值相比,基于混合卡尔曼滤波器的前轮转角预估值最大误差为0.23°,均方根误差为0.12°。
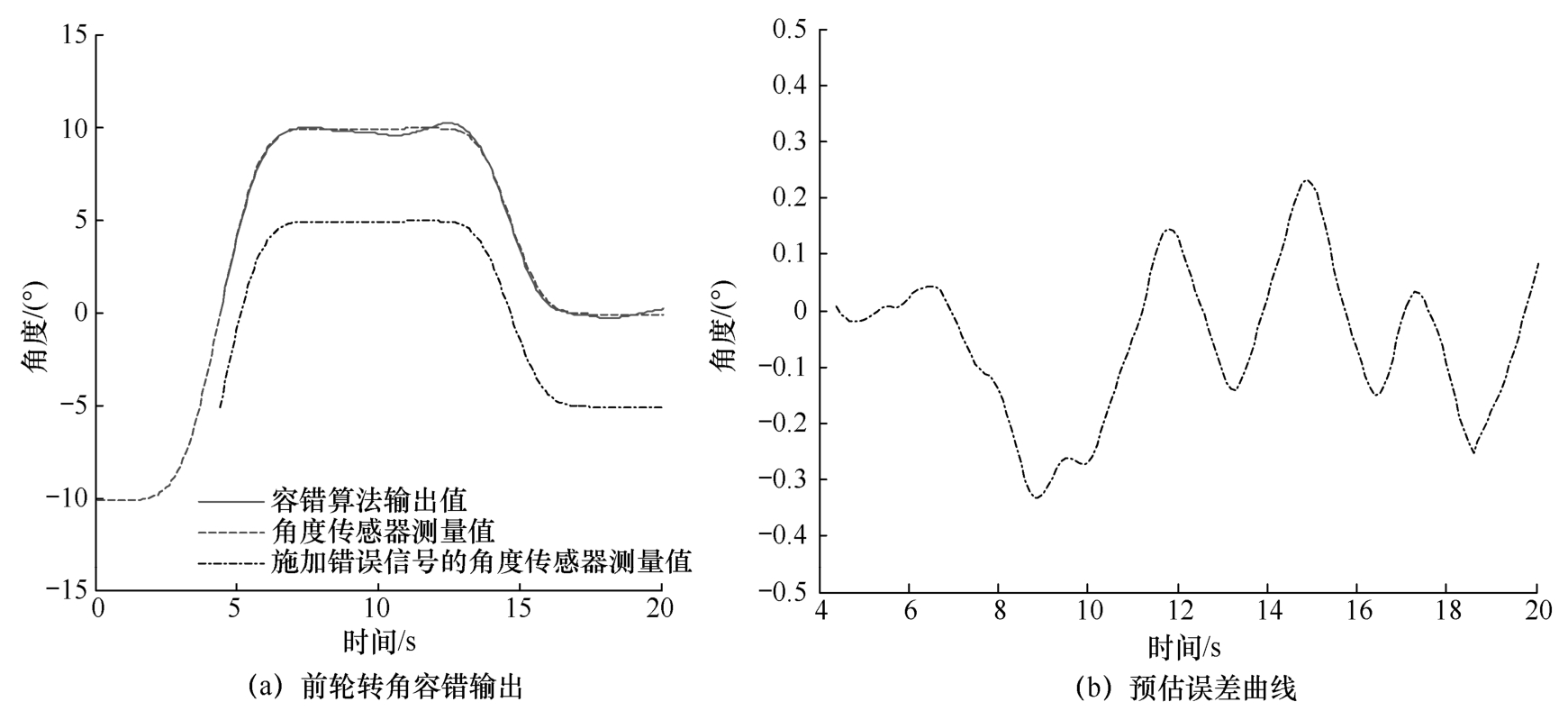
图2-20 基于混合卡尔曼滤波器的前轮转角信息融合测量试验结果
试验结果表明,混合卡尔曼滤波器数据融合方法具有一定的可行性,当前轮角度传感器发生故障时,融合测量方法的输出值可以代替前轮角度编码器工作,有助于提高拖拉机自动转向控制系统的自适应能力。