




(1)第一个光化学定律——只有被吸收的光才对光化学过程是有效的,这是Grotthus和Draper于19世纪总结的第一个光化学定律。
(2)光化学反应过程 [10]
分子、原子、自由基或离子吸收光子而发生的化学反应,称为光化学反应。化学物种吸收光量子后,可产生光化学反应的初级过程和次级过程。
初级过程包括化学物种吸收光量子形成激发态物种,其基本步骤为:
式中:A * 为物种A的激发态; hv 为光量子。
随后,激发态A * 可能发生如下几种反应:
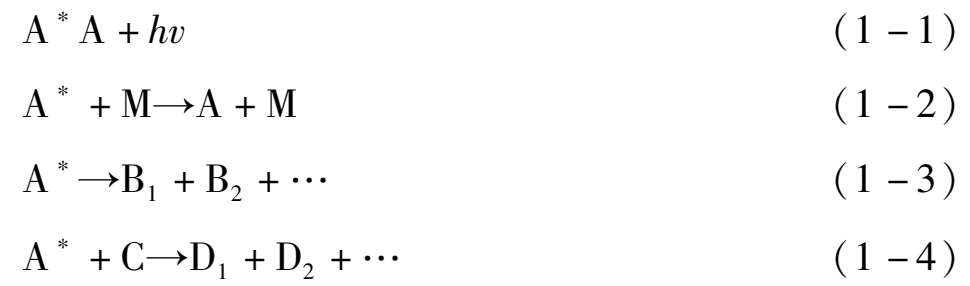
式(1-1)为辐射跃迁,即激发态物种通过辐射荧光或磷光而失活。式(1-2)为无辐射跃迁,亦即碰撞失活。激发态物种通过与其他分子M碰撞,将能量传递给M,本身又回到基态。以上两种过程均为光物理过程。式(1-3)为光离解,即激发态物种离解成为两个或两个以上新的物种。式(1-4)为A * 与其他分子反应生成新的物种。这两种过程均为光化学过程。
次级过程是指在初级过程中反应物、生成物之间进一步发生的反应。如氯化氢的光化学反应过程:

式(1-5)为初级过程。式(1-6)为初级过程产生的H与HCl反应。式(1-7)为初级过程产生的Cl之间的反应,该反应必须有其他物种如O 2 或N 2 等存在下才能发生,式中用M表示。式(1-6)和式(1-7)均属次级过程,这些过程大都是放热反应。
根据光化学第一定律,首先,只有当激发态分子的能量足够使分子内的化学键断裂时,亦即光子的能量大于化学键能时,才能引起光离解反应。其次,为使分子产生有效的光化学反应,光还必须被所作用的分子吸收,即分子对某种特定波长的光要有特征吸收光谱,才能产生光化学反应。
(3)光化当量定律——一个分子吸收一个光子而被活化,或者说分子吸收光的过程是单光子过程。它也被称为Einstein定律。这个定律基础是电子激发态分子的寿命很短,约为10 -8 s,在这样短的时间内,辐射强度比较弱的情况下,再吸收第二个光子的概率很小。当然若光很强,如高通量光子流的激光,即使在如此短的时间内,也可以产生多光子吸收现象,这时Einstein定律就不适用了。
分子吸收光子,电子跃迁至高能态,产生电子激发态分子。现在需要知道的是,电子被激发至何能态以及激发态分子的能量为何?
电子跃迁时分子的重度M(multiplicity)起重要作用,按定义M=2S+1,S为分子中电子的总自旋量子数,M代表分子中电子的总自旋角动量在z方向上的分量的可能值。如果分子中电子自旋都是成对的,S=0,因此,M=1,这种状态被称为单线态(singlet state)或S态。对大多数分子(O 2 及S 2 例外),特别是对绝大多数的有机化合物分子而言,基态分子中电子自旋是成对的,因此分子的基态大多数为单线态或S态(以S 0 表示之)。
在考虑电子跃迁时,我们只考虑激发时涉及的那一对电子,假设其他电子状态在激发时不变,这样就将出现两种可能的情况:
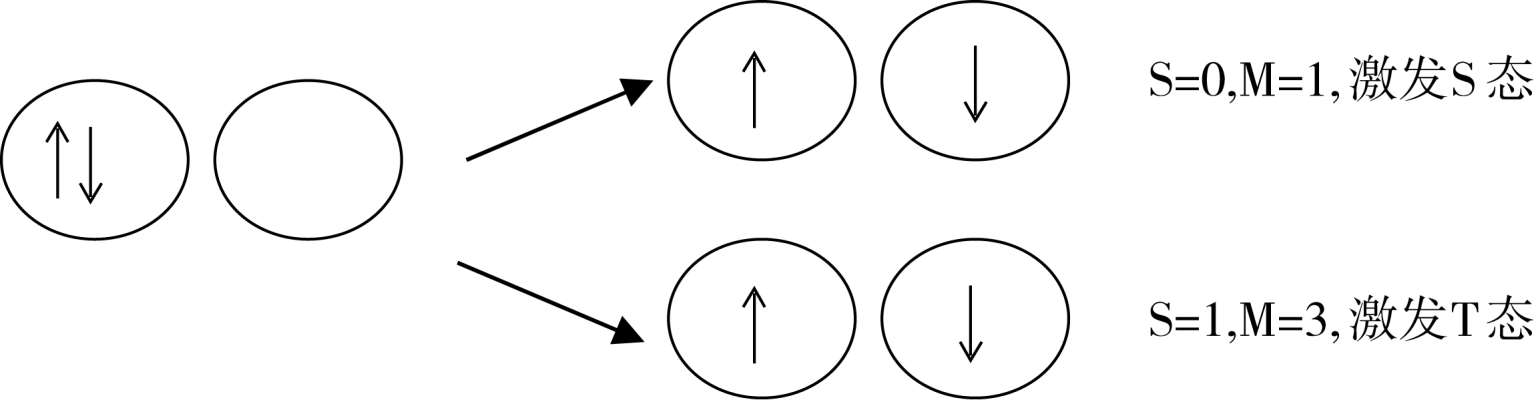
如果被激发至空轨道的电子的自旋与原先在基态轨道的方向相同,则激发态的S=0,M=1,此种电子激发态仍属S态,按其能量的高低可以以S 1 ,S 2 ,…表示之。如果受激电子的自旋方向与原在基态的相反,产生了在两个轨道中的自旋方向平行的两个电子,则S=1,M=3,此种态被称作三线态(triplet state)。因为在磁场中,分子中电子的总自旋角动量在磁场方向可以有三个不同值的分量,因此,三线态是三度简并的态,以T表示,按能量高低可有T 1 ,T 2 ,…激发T态。
由于在三线态中,两个处于不同轨道的电子的自旋平行,两个电子轨道在空间的交盖较少,电子的平均间距变长,因而相互排斥的作用降低,所以T态的能量总比相应的S态为低(图1-4)。
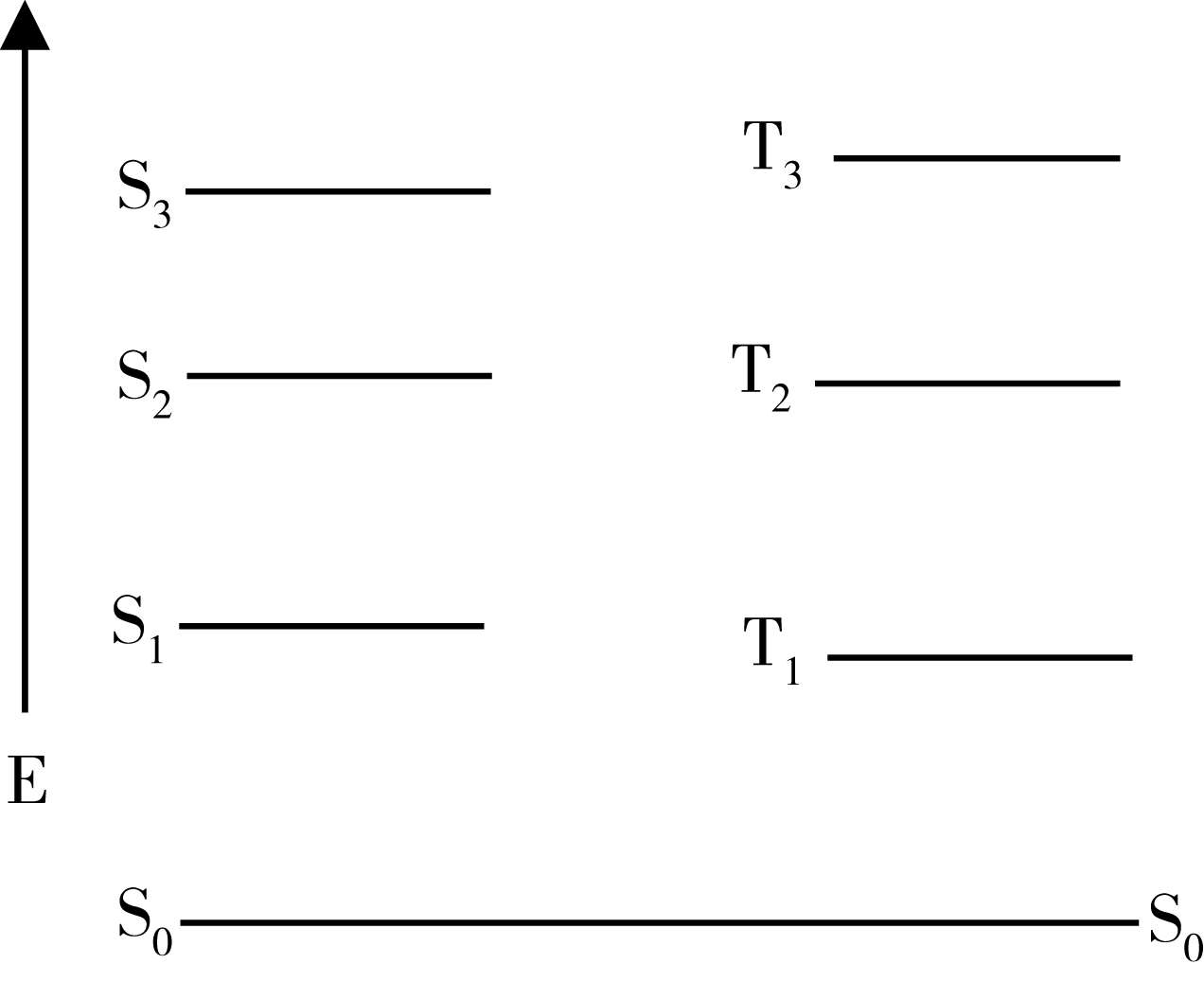
图1-4 电子跃迁能级图
电子跃迁光谱的谱带的位置决定于电子在n和m两态间跃迁的能量差,即 ΔE = E m - E n , m > n ,而谱带的强度则与许多因素有关。
光谱带的强度不同是由于电子的跃迁概率不同。高强度谱带有大的跃迁概率,这种跃迁被称为是允许的(allowed);强度弱的谱带的跃迁概率小,这种跃迁被称为是禁阻的(forbidden)。
和其他光谱一样,在电子光谱中从理论和实验结果可以得出一些选择定则(selectionrules),它告知何种跃迁是禁阻的,何者为允许的。
一种电子跃迁是允许的还是禁阻的决定于跃迁过程中分子的几何形状和动量是否改变、电子的自旋是否改变、描述分子轨道的波涵数是否对称以及轨道空间重叠程度。
分子中的电子跃迁时伴随有转动和振动能级的变化,这种变化构成了吸收光谱的振动精细结构。与电子跃迁不同,从分子中的一个电子态至另一个电子态时,对振动能级的变化没有选则,因而从基态 S 0 的 v =0振动能级至 S 1 态中任何一个振动能级的跃迁均为可能,但是振动精细结构中各谱线的相对强度都可以由Franck-Condon原则来决定。
用双原子分子的光谱最容易说明Franck-Condon原则,它可以推广至多原子分子的情况。
Franck-Condon原则认为:相对于双原子分子的振动周期(约为10 -13 s)而言,电子跃迁所需的时间是极短的(约为10 -15 s)。因此,在电子跃迁的瞬间内,核间距和速度都可以是固定不变的。
图1-5给出了双原子分子的基态和第一激发态的势能曲线,横坐标为核间距,纵坐标为势能。由于激发态比基态的稳定性差,因此激发态的势能曲线一般都位于基态的右上方;而且,电子被激发时跃迁至推斥的反键轨道,所以激发态的势能曲线一而言均向大的核间距方向偏移。按照Franck-Condon原则,分子被由基态激发至第一激发态时,必然沿着垂直于核间距坐标的线跃迁(图1-5中箭头所示方向),这种跃迁可称为Franck-Condon跃迁。
图1-5(a)中电子激发态的平衡核间距与基态的相似。根据Franck-Condon原则,只有从基态的 v =0振动能级至激发态的 v′ =0振动能级的跃迁(0→0跃迁)概率最大;由于从基态的 v =0至激发态的 v′ =1,2,…振动能级跃迁时,核间距要依次发生相当的变化,所以,在这种情况下,振动谱线以0→0跃迁的强度最大。在图1-5(b)中,根据Franck-Condon原则可以预言,不是0→0跃迁,而是01跃迁谱线的强度最大[图1-5中(e)]。有时激发态的平衡核间距位移如此之大,以致由基态 v =0出发的Franck-Condon跃迁与激发态势能曲线相交于离解渐进线之上[图1-5中(c)]。这是因为电子被激发后,分子应立即进行振动,此时原子间已无回收力,因而分子立即离解为原子。在这种情况下,向渐进线以下的不连续跃迁虽然是可能的,但强度不大[图1-5中(f),0→m,0→m-1等];向渐进线以上的跃迁由于没有量子化条件的限制(能量不是分立的),而呈现为连续的吸收谱。这时电子跃迁导致分子的离解,至少离解产物之一处于激发态。
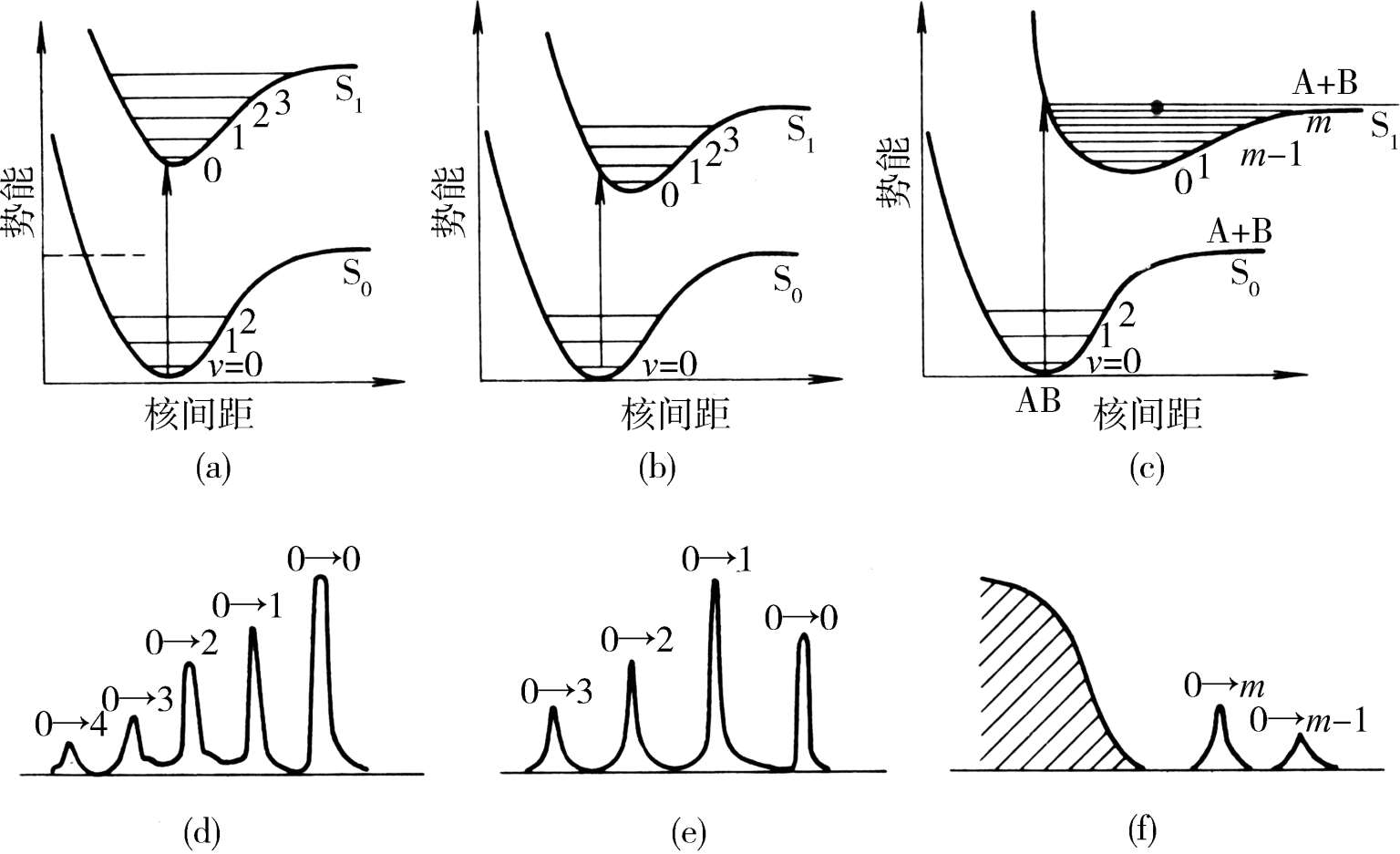
图1-5 双原子分子电子跃迁势能曲线相应的振动精细谱带
Franck-Condon原则也适用于发射过程。由于在凝聚相中,激发态之间的振动能及电子能弛豫过程的速率比发射辐射的速率快得多,因此发射辐射总是从最低激发态的v′=0振动态出发的[图1-6中(a)],图1-6中(b)示出相应的发射Franck-Condon跃迁。根据Franck-Condon原则,最可几的发射是自S 1 态的v′=0垂直发射的;与吸收相反,基态势能曲线的最低点现在位于最低激发态势能曲线的最小点的左方,因此最可几发射将产生一个伸长了的基态,而吸收时随着跃迁产生一个压缩了的激发态,图1-6中(b)示出了发射谱振动结构的相对强度。
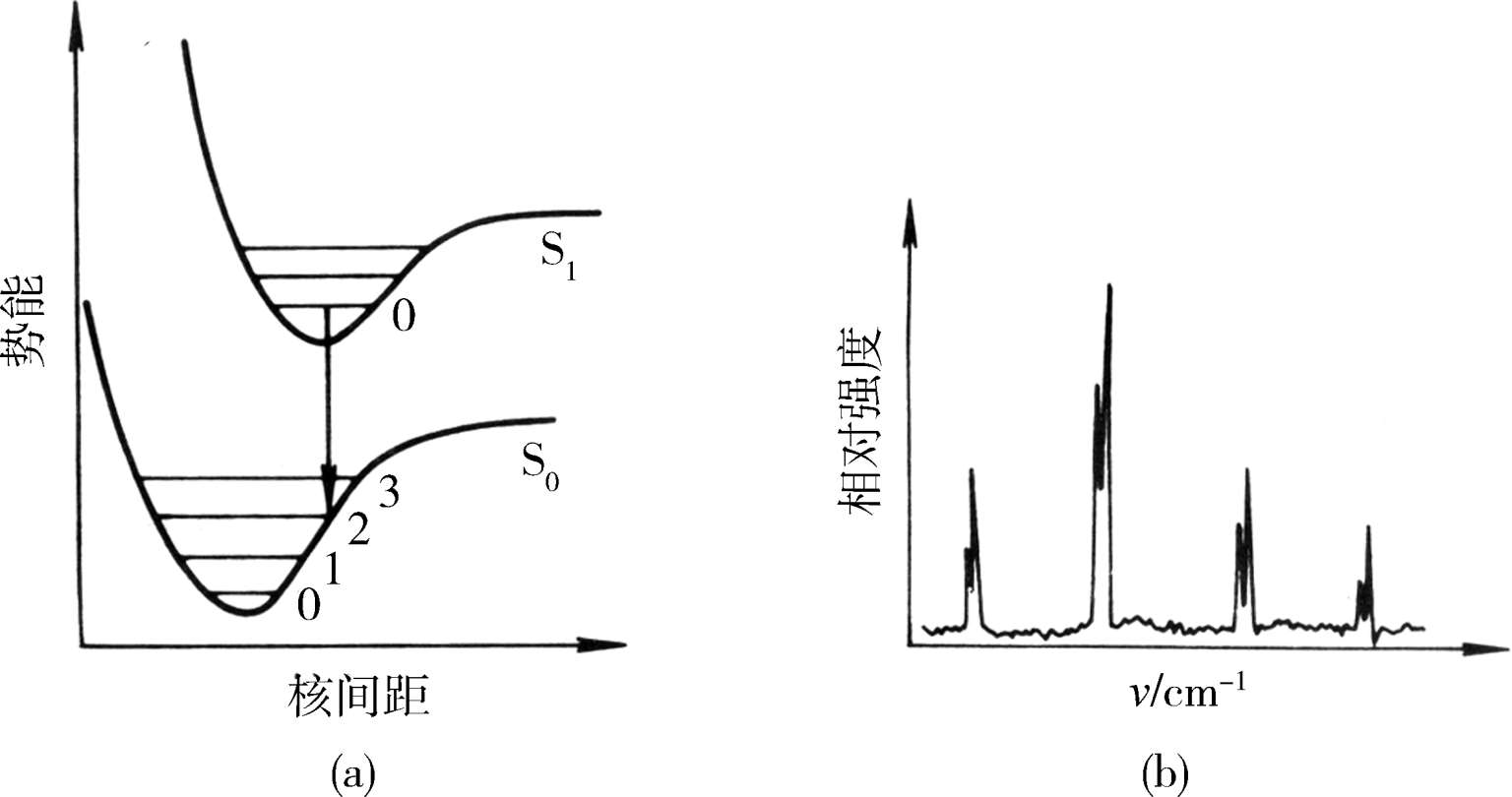
图1-6 发射过程的Franck-Condon跃迁
在电子跃迁过程中电子的自旋不能改变,符合这一规则的跃迁,如单重态→单重态、三重态→三重态跃迁是允许的,违背这一规则的跃迁,如单重态→三重态和三重态→单重态跃迁是禁阻的。
宇称禁阻由跃迁所涉及的轨道的对称性决定,分子轨道的对称性取决于描述分子轨道的波函数在通过一个对称中心反演时符号是否改变。波函数分为对称的( g )和反对称的( u )两类。通过对称中心反演,分子轨道的波函数改变符号,称为反对称的;如果不改变符号,称为对称的。选择定则指出 u → g 和 g → u 的跃迁是允许的,而 g → g 和 u → u 的跃迁是禁阻的。例如,乙烯的分子中, π 轨道是反对称的, π * 是对称的, σ 轨道是对称的,因此,乙烯的 π → π * ( u → g )跃迁是允许的,而 σ → π * ( g → g )跃迁是禁阻的,如图1-7所示。
如果电子跃迁涉及的两个轨道在空间的同一区域,即相互重叠,这种跃迁是允许的,否则是禁阻的。例如羰基化合物的π→π * 跃迁是允许的,而n→π * 跃迁是禁阻的。
一种电子跃迁,只有被上述所有选择定则允许,这种跃迁才是允许的;如果被其中一个选择定则禁阻,这种跃迁发生的可能性就很小。
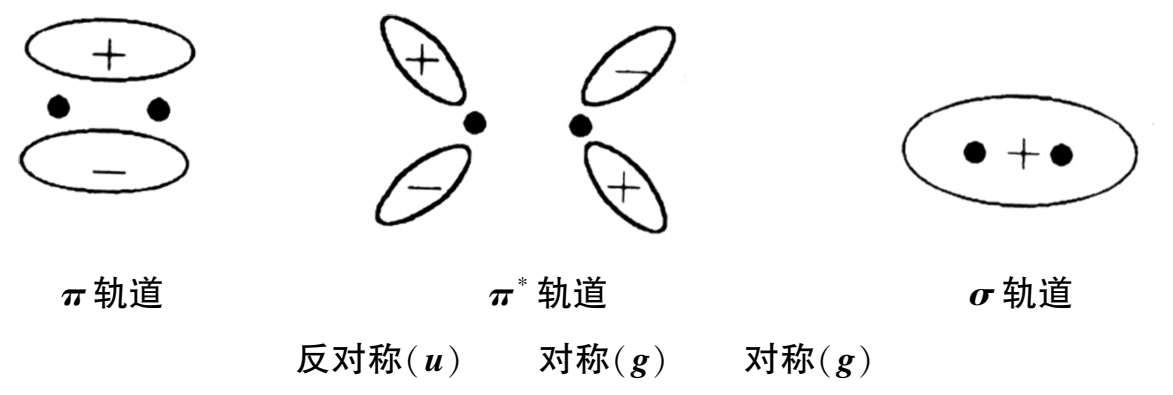
图1-7 乙烯分子轨道
基态分子吸收一个光子生成单重激发态,依据吸收光子的能量大小,生成的单重激发态可以是S 1 ,S 2 ,S 3 ,…,由于高级激发态之间的振动能级重叠,S 2 、S 3 等会很快失活到达最低单重激发态S 1 ,这种失活过程一般只需10 -13 s,然后由S 1 再发生光化学和光物理过程。同样,高级三重激发态(T 2 ,T 3 ,…)失活生成最低三重激发态T 1 也很快。所以,一切重要的光化学和光物理过程都是由最低激发单重态(S 1 )或最低激发三重态(T 1 )开始的,这就是Kasha规则。
激发态分子失活回到基态可以经过以下光化学和光物理过程:辐射跃迁、无辐射跃迁、能量传递、电子转移和化学反应。
分子由激发态回到基态或由高级激发态到达低级激发态,同时发射一个光子的过程称为辐射跃迁,包括荧光和磷光。
荧光是多重度相同的状态间发生辐射跃迁产生的光,这个过程速度很快。有机分子的荧光通常是S 1 →S 0 跃迁产生的,虽然有时也可以观察到S 2 →S 0 (如某些硫代羰基化合物)的荧光。当然由高级激发三重态到低级激发三重态的辐射跃迁也可以产生荧光。
磷光是不同多重度的状态间辐射跃迁的结果,典型跃迁为T 1 →S 0 ;而T n →S 0 则很少见。因为这个过程是自旋禁阻的,因此和荧光相比,其速度常数要小得多。
激发态分子回到基态或高级激发态到达低级激发态,但不发射光子的过程称为无辐射跃迁。无辐射跃迁发生在不同电子态的等能的振动-转动能级之间,即低级电子态的高级振动能级和高级电子态的低级振动能级间耦合,跃迁过程中分子的电子激发能变为较低级电子态的振动能,由于体系的总能量不变,不发射光子。这种过程包括内转换和系间窜越。
内转换是相同多重度的能态之间的一种无辐射跃迁,跃迁过程中电子的自旋不改变,如S m ~ TM S n 或T m ~ TM T n ,这种跃迁是非常迅速的,只需10 -12 s。
系间窜越是不同多重度的能态之间的一种无辐射跃迁。跃迁过程中一个电子的自旋反转,例如,S 1 ~ TM T 1 或T 1 ~ TM S 0 。
激发态分子另一条失活的途径是能量传递,即一个激发态分子(给体D * )和一个基态分子(受体A)相互作用,结果给体回到基态,而受体变成激发态的过程:
能量传递过程也要求电子自旋守恒,因此只有下述两种能量传递具有普遍性:
单重态-单重态能量传递:D * (S 1 )+A(S 0 )→D(S 0 )+A * (S 1 )
三重态-三重态能量传递:D * (T 1 )+A(S 0 )→D(S 0 )+A * (T 1 )
激发态的分子可以作为电子给体,将一个电子给予一个基态分子,或者作为受体从一个基态分子得到一个电子,从而生成离子自由基对:
激发态分子的HOMO上只填充了一个电子,很容易再接受另一个电子;另一方面,LUMO上的高能电子很容易给出,所以,许多情况下,与基态分子相比,激发态分子既是很好的电子接受体,又是很好的电子给体,这就使得电子转移成为激发态失活的一条非常重要的途径。
激发态分子失活的一条最重要的途径是发生化学反应生成基态产物,这一过程是光催化降解化合物的主要内容,在以后介绍。
上述激发态失活的过程可总结在Jablonski图中,该图表示出体系状态转变时可能出现的光化学和光物理过程(图1-8)。
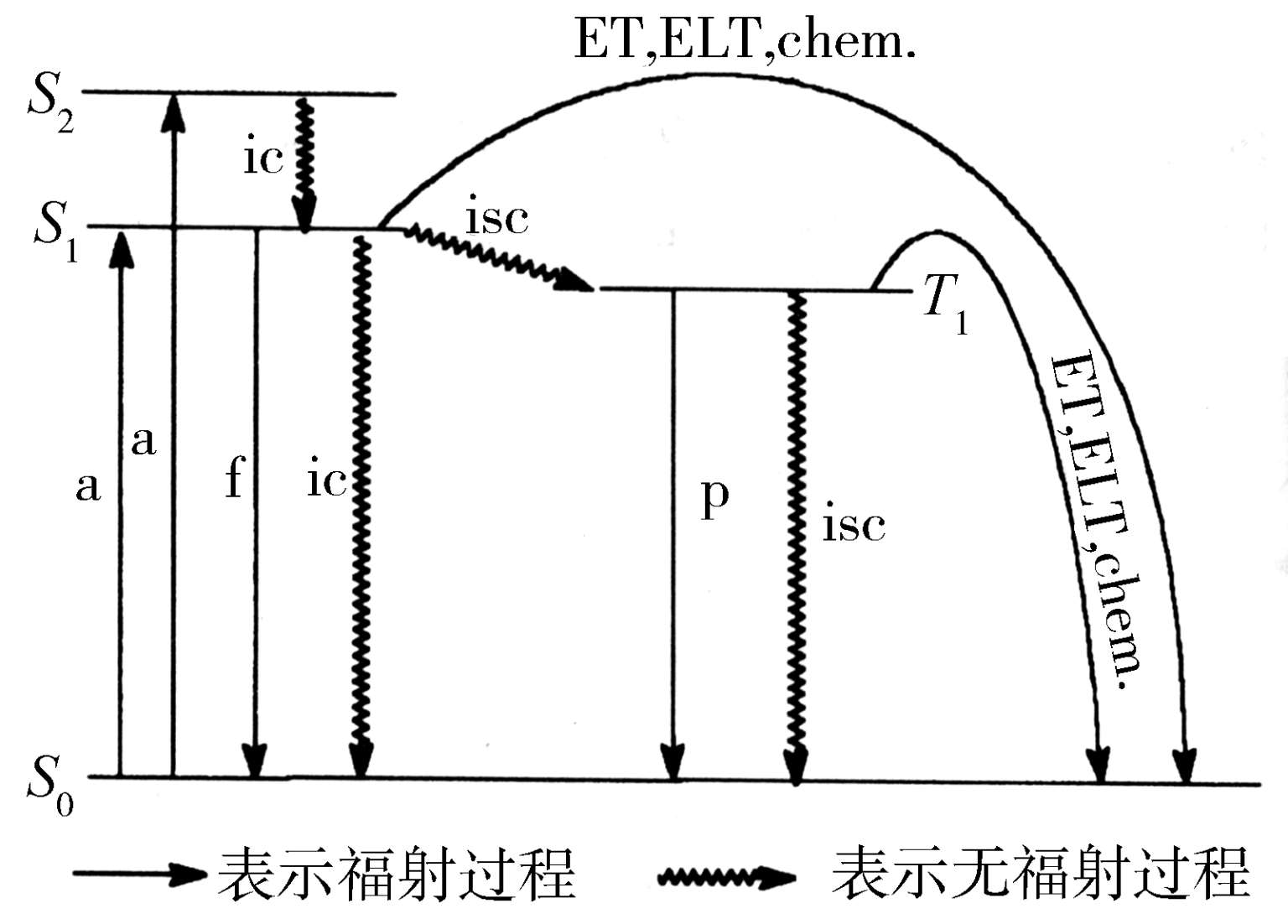
图1-8 Jablonski图解
(a)吸收;f—荧光;p—磷光;ic—内转换;isc—系间窜越;ET—能量传递;ELT—电子转移;chem .—化学反应