
下载掌阅APP,畅读海量书库
立即打开




由图 4-3 可以看出,初二和高三学生答题各有千秋,二者答题大致走向基本相同。看不出重要差别。因而需进一步作独立样本T检验。
表4-4 初二学生、高三学生独立样本T检验
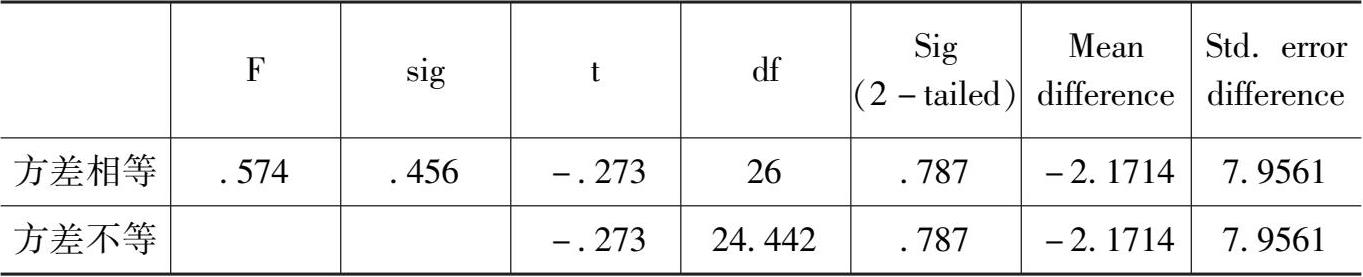
从表中可以看出,T统计量的相伴概率 0.787 大于显著性水平 0.05,不能拒绝T检验的零假设,即初二学生和高三学生的朴素认识不存在显著性差异。
为了进一步验证笔者的猜想,笔者对初二和大二学生作独立样本T-检验。
表4-5 初二、大二学生朴素认识独立样本T-检验
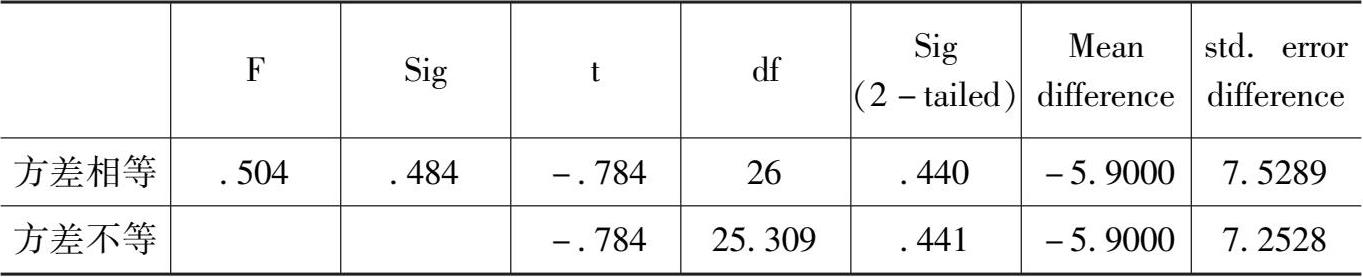
从表 4-5 中可以看出,T统计量的相伴概率-0.784 大于显著性水平0.05,不能拒绝T检验的零假设,即初二学生和大二学生的朴素认识不存在显著性差异。
统计结果说明,学生通过四年学习,年龄和数学知识增长了,但对无限的朴素认识变化不大。学生对无限的朴素认识和数学知识以及年龄并无显著关系。笔者分析原因有二:
无论是表面理解还是本质理解,都定位于个体对无限的感官认识,这种感官认识是学生内在的、固有的认识,是多年生活经验累积结果,和学生的数学知识的增长关系不大,是无限的认识本原。横向比较来看,感官认识存在个体差异性,和个体认识事物的角度、方式有关。
朴素认识的心理模式是以生活经验为判断依据。时间和空间的无限性,促使学生形成无限认知模式。模式一旦形成,很难改变。尽管数学知识增长了,年龄增加了,但学生对无限的朴素认识却没有较大改变。