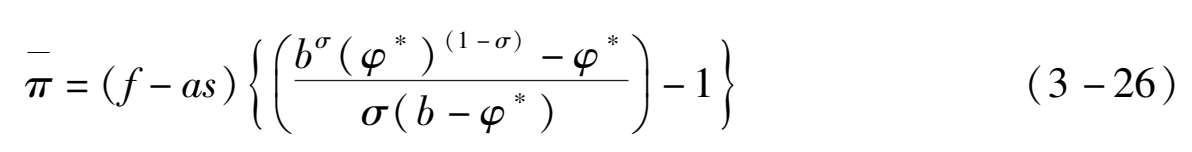四、封闭条件下制造业部门的生产均衡

在制造业产品的生产中，企业的生产以规模收益递增和垄断竞争为主要特征，假定每个企业都使用单一生产要素劳动力来生产单一的某种差异化产品，同时，企业的生产技术由企业的成本函数来表征。成本函数的形式如下：

其中， l 为生产 q 单位工业产品所需要的劳动力投入， s 和 f － as 分别代表了产业的集聚水平和工业品生产所必须投入的沉淀成本。其中， a 为一大于零的常数，减号的形式则说明，随着产业集聚水平的提高，企业的沉淀成本有所降低，这样的一个假设是与Greenaway和Kneller（2008）、Clerides et al（1998）研究得出的结论是相一致的。在工业品的生产中，虽然所有企业面临着相同的沉淀成本，但他们的生产效率并不相同。这一点，由生产率 φ 的变化情况来体现。作为生产率的衡量指标， φ 的大小反映了生产单位产品所需的边际劳动力投入的多少。在本文的分析中，本文认为企业在进入工业品生产市场之前，只知道生产率的分布情况，而不确切知道他们本身的生产率的大小。在此，本文假定生产率 φ 的分布满足概率为 F （ φ ）＝ φ/b ，均值为 ζ 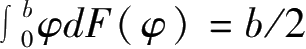＝ 的分布函数，其中 b 为一个足够大的正数。

为了求得封闭条件下制造业部门生产厂商的均衡情况，首先需要求得制造业产品的生产价格。考虑厂商的利润最大化问题，第 i 个厂商的利润函数为：

利润最大化的一阶条件为：

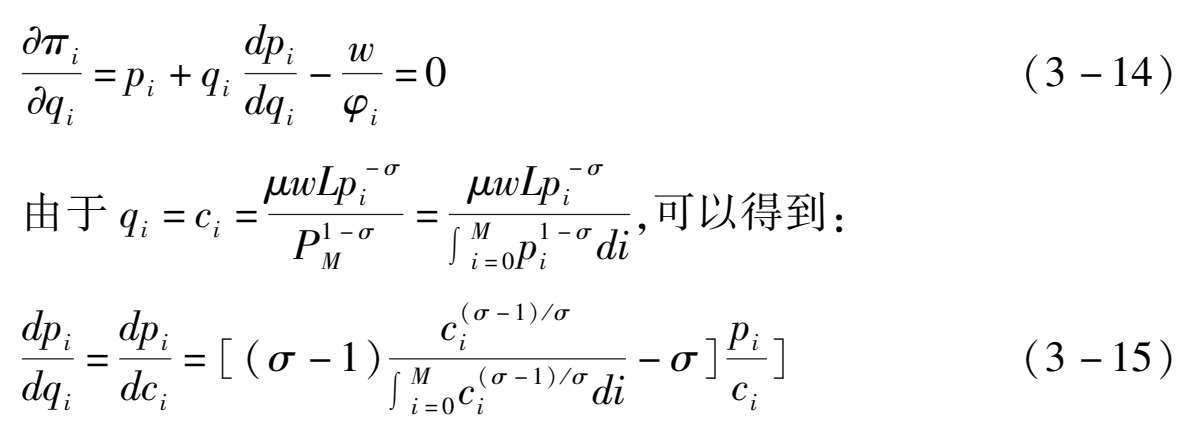
由于众多企业具有彼此对称的特征，这意味着：

c _i ＝ c ， i ＝1，2，… M ，继而有：

由（3－14）式、（3－15）式以及（3－16）式，可以求得制造业产品的生产价格以及最优的产出，分别为（3－17）式和（3－18）式：

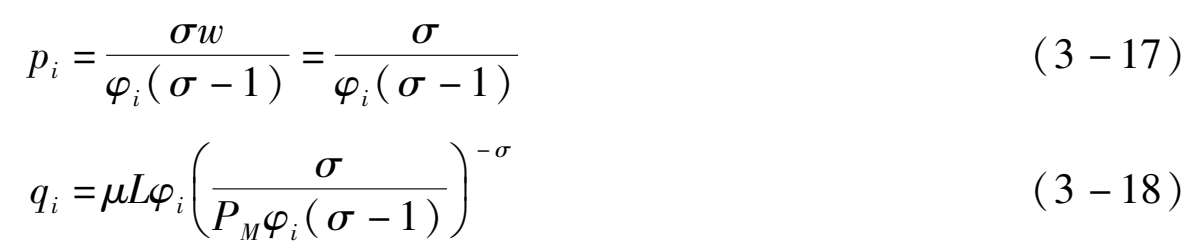
在生产价格已知的情况下，可以求得第 i 个厂商的收益函数和利润函数，分别为（3－19）式和（3－20）式：

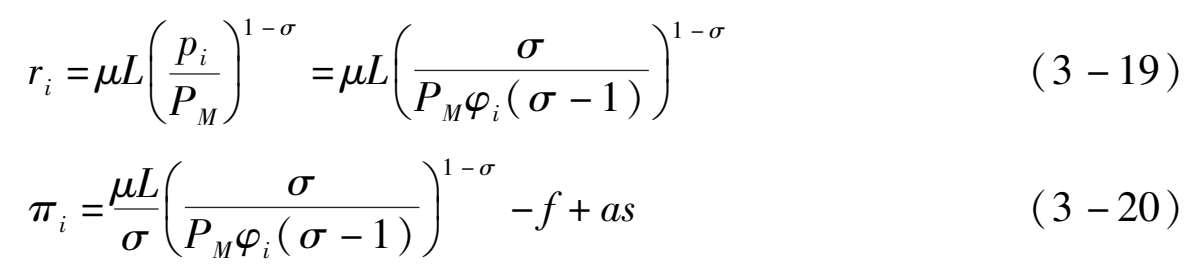
由（3－20）式可以看出，企业的利润水平与生产率的高低相关，较高的生产率与较高的企业利润是相对应的。同时，由于只有在企业的生产利润非负时，企业才进行生产，为了对此进行表征，可以定义企业停止生产的生产率临界值为 φ ^* ，此时，有 π （ φ ^* ）＝0。同时，为了衡量均衡时整个行业的平均生产率，定义全部行业的均衡生产率为：

由于企业的利润水平与生产率的高低正相关，在均衡时，只有生产率处于区间（ φ ^* ， b ）内的企业才能进行生产，所以在生产均衡时市场上厂商的平均生产率可以修正为：

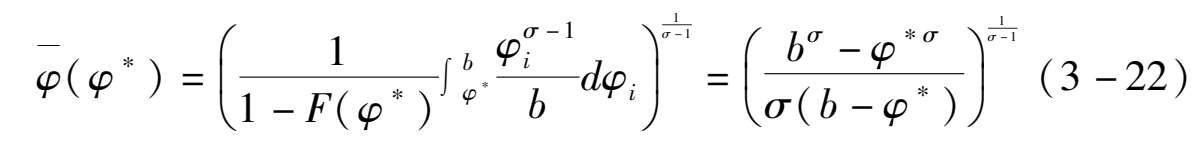
同时，由（3－19）式可知，不同企业总收益的比值仅与这些企业生产率的相对大小有关，即：

因此，在代表性企业的生产率恰好等于行业的平均生产率的情况下，整个行业的平均利润可以由代表性企业的利润来表示，即：

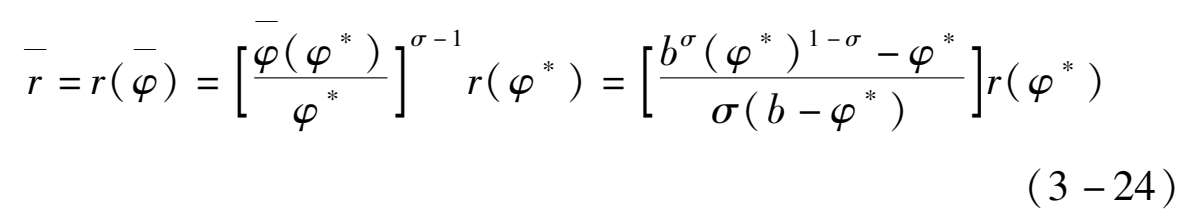
相应的，行业的平均利润如下：

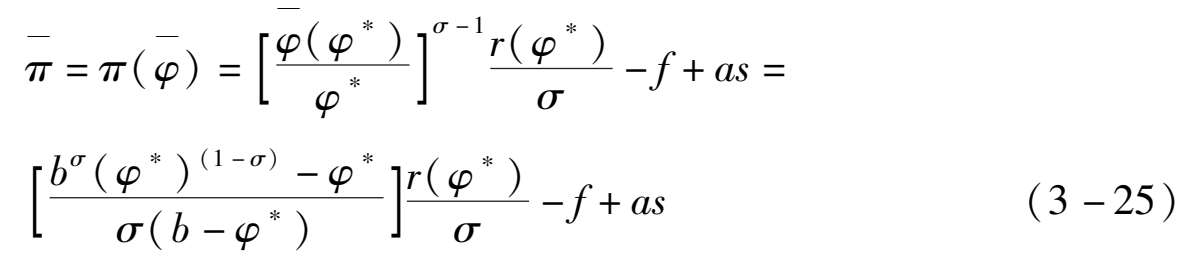
同时，由于 π （ φ ^* ）＝0，这意味着 r （ φ ^* ）＝ σ （ f － as ），因此可以将行业的平均利润进一步写为： oLLWUWVfJnok2jKdzR31/LjBqHLphB9ybfTeAHKTfPhDlsX2Icbj/jF2Ag9kSIQN