二、消费均衡

消费者同时消费农产品和差异化的制造业产品，其消费函数的形式如下： U ＝

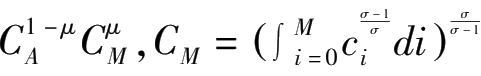
其中， C _M 表示消费者对制造业产品的消费组合， C _A 表示消费者对农产品的消费， μ 和1－ μ 分别代表消费者在制造业产品和农产品上的支出份额。由于制造业产品是多样化的异质产品，消费者对其的消费是对某种制造业产品组合的消费，它的消费函数是不变替代弹性的， σ 表示不同制造业产品之间相对不变的消费替代弹性，其大小满足0＜ μ ＜1＜ σ 。 c _i 则是消费者对制造业产品消费组合中第 i 种制造业产品的消费数量。

首先考虑如下形式的本国消费者效用最大化问题：

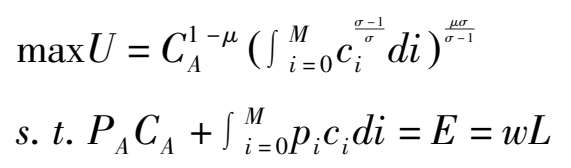
其中， P _A 和 p _i 分别表示农产品和第 i 种制造业产品的价格， E 为居民全部要素收入。为了求解上式，建立拉格郎日函数如（3－1）式：

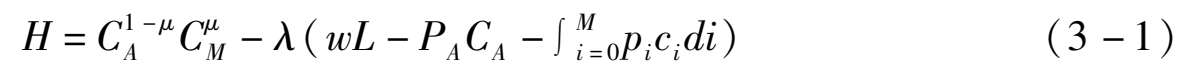
求解 c _i 的最优一阶条件，可得：

同理，求解 c _j 的最优一阶条件可以得到：

由（3－2）式和（3－3）式，可得：

即：

将 C _M 的表达式代入（3－5）式，可得：

将其代入制造业产品的总支出函数，并整理可得：

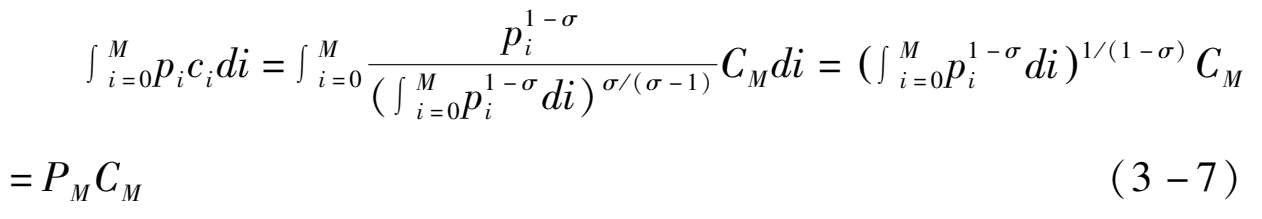
其中， PM 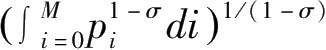＝ ，反映了制造业产品的价格指数。将其代入（3－6）式，可以得到制造业产品的需求函数为：

重新考虑消费者的效用最大化问题：

代人需求函数（3－8）式，可得：

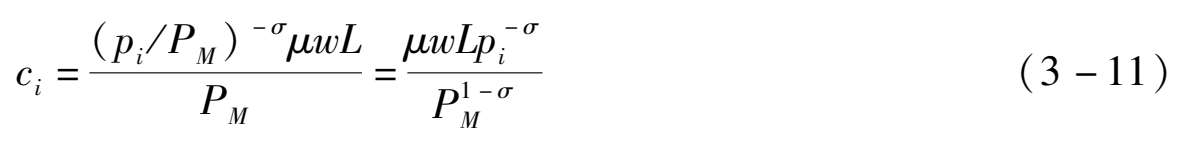
上式即为最终的消费者对制造业产品的需求函数。 r07/3yvNGhCHaMcoxpUGPHRZ6NODv77UwQaC5khFkA9PVXhxHFzTygKPrOKwDJP8