




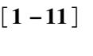
在激光器中所有能量都是增益介质通过受激发射光子的形式而释放出来的,光子的受激发射与晶格中振动能量(声子)的发射存在耦合时,就可以实现可调谐发射。在这种电子振动的激光器中,激光跃迁的总能量是固定的,但可以连续地分配在各个声子上,因此激光输出波长的调谐范围可以很大。
过渡金属离子之所以能在基质晶体中产生宽带发射,主要是由激活离子本身的性质及其所处晶体场对激活离子的影响来决定的。过渡金属离子电子组态为
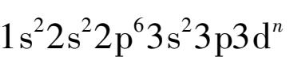 (
n
= 1 ~ 9),在离子固体中失去最外层的电子形成+ 2,.3,.4 价的离子。由于3d
n
壳层中的电子没有外壳层的屏蔽,电子运动受晶体场和晶格振动的影响较大,激发态与基态之间位形坐标的原点有较大位移,发射和吸收谱包括了多声子跃迁的边带,形成了较宽的吸收带和荧光发射带。
(
n
= 1 ~ 9),在离子固体中失去最外层的电子形成+ 2,.3,.4 价的离子。由于3d
n
壳层中的电子没有外壳层的屏蔽,电子运动受晶体场和晶格振动的影响较大,激发态与基态之间位形坐标的原点有较大位移,发射和吸收谱包括了多声子跃迁的边带,形成了较宽的吸收带和荧光发射带。
晶体场的作用可用静态和动态两种作用进行解释。静态作用是指晶体场强度随激活离子和配位离子之间距离的变化而变化的关系。动态作用是指电子-声子耦合作用,即过渡金属离子的外层电子与基质晶体的晶格振动-声子发生耦合作用。
晶体场,顾名思义即晶格产生的电场,它与晶体结构和离子组成有关。晶体场的主要作用有三个:(1)使宇称选择定则放松;(2)使离子能级产生分裂;(3)使简并度部分或全部消除。
晶体场理论只考虑中心离子和配体之间的静电相互作用,将离子和周围配体间的相互作用简化为单个离子与周围配体的静电作用,着眼点是中心离子d轨道在周围配位体影响下的能级分裂。电子在分裂了的轨道上的排布状态,决定了配位场的光谱、磁性、稳定性和几何构型等性质。固体中过渡金属离子的最外层电子组态为 3d n ,即最外层的价电子是 n 个d电子。在自由离子状态时,这些d电子都是处在 3d轨道中, d轨道是五重简并,即有五个相同的能量d轨道。在固体中,由于晶体场的非对称性分布,这五个d轨道的对称性发生变化,因此能量就不再完全相同,能级发生分裂,简并度降低。过渡金属离子在晶格中一般呈八面体或四面体配位,下面以正八面体晶体场( O h )为例解释一下过渡金属离子d轨道能级的分裂。
自由金属离子在带负电荷的晶体场中所受的作用,可定性地分为球对称部分和场对称部分。负电场的静电排斥作用对所有d轨道是相同的,使所有的d轨道能级都上升
E
s
。正八面体配合物中d轨道的能级分裂选取如图 2.1 所示的坐标轴。6 个配位体沿着三个坐标轴正、负方向(.
x
, .
y
, .
z
)接近中心离子,根据五个d轨道在空间的取向可以看出,负电荷对
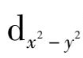 和
和
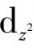 轨道的电子排斥作用大,使这两轨道的能级上升,而
轨道的电子排斥作用大,使这两轨道的能级上升,而
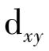
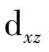
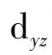 轨道夹在坐标轴之间,受到的排斥较小,能级降低,这样d轨道分裂成两组:一组是能量较高的
轨道夹在坐标轴之间,受到的排斥较小,能级降低,这样d轨道分裂成两组:一组是能量较高的
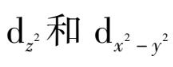 (二重简并),另一组是能量较低的
(二重简并),另一组是能量较低的
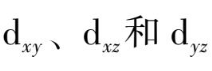 (三重简并)。
(三重简并)。
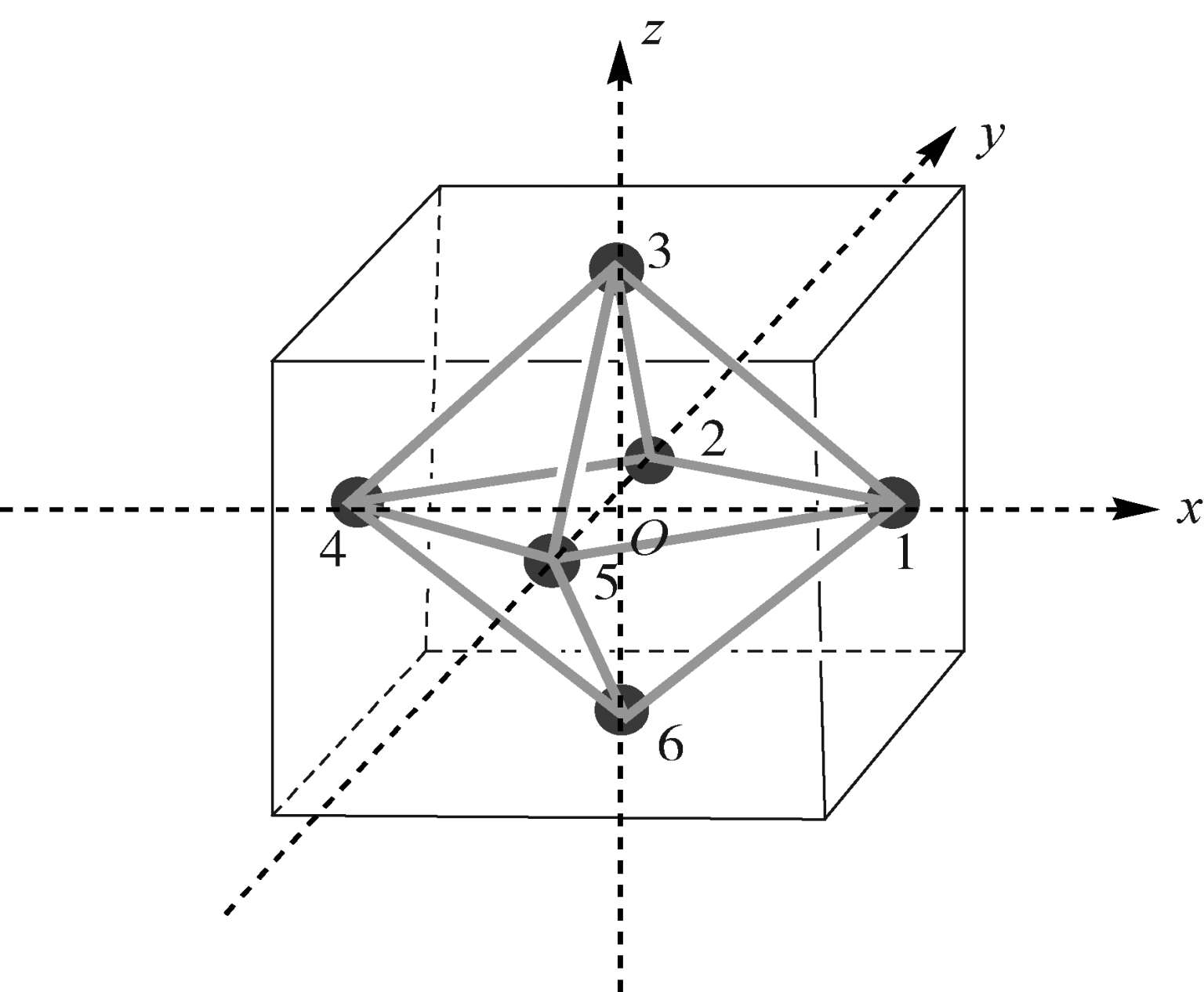
图2.1 正八面体及其坐标
在正八面体
O
h
群中,
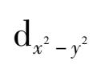 ,
,
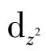 同属e
g
不可约表示( e表示二重简并, g表示中心对称)。
同属e
g
不可约表示( e表示二重简并, g表示中心对称)。
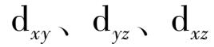 同属
同属
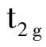 不可约表示(t表示三重简并,2 表示第 2 组).e
g
和t
2
g的能级差为Δ0(或 1.
D
q
),称为分裂能。根据量子力学中的重心不变原则可计算出八面体场中e
g
能级上升 6
D
q
,
不可约表示(t表示三重简并,2 表示第 2 组).e
g
和t
2
g的能级差为Δ0(或 1.
D
q
),称为分裂能。根据量子力学中的重心不变原则可计算出八面体场中e
g
能级上升 6
D
q
,
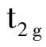 能级下降 4
D
q
(与
E
s
能级相比),如图 2.2所示。
能级下降 4
D
q
(与
E
s
能级相比),如图 2.2所示。
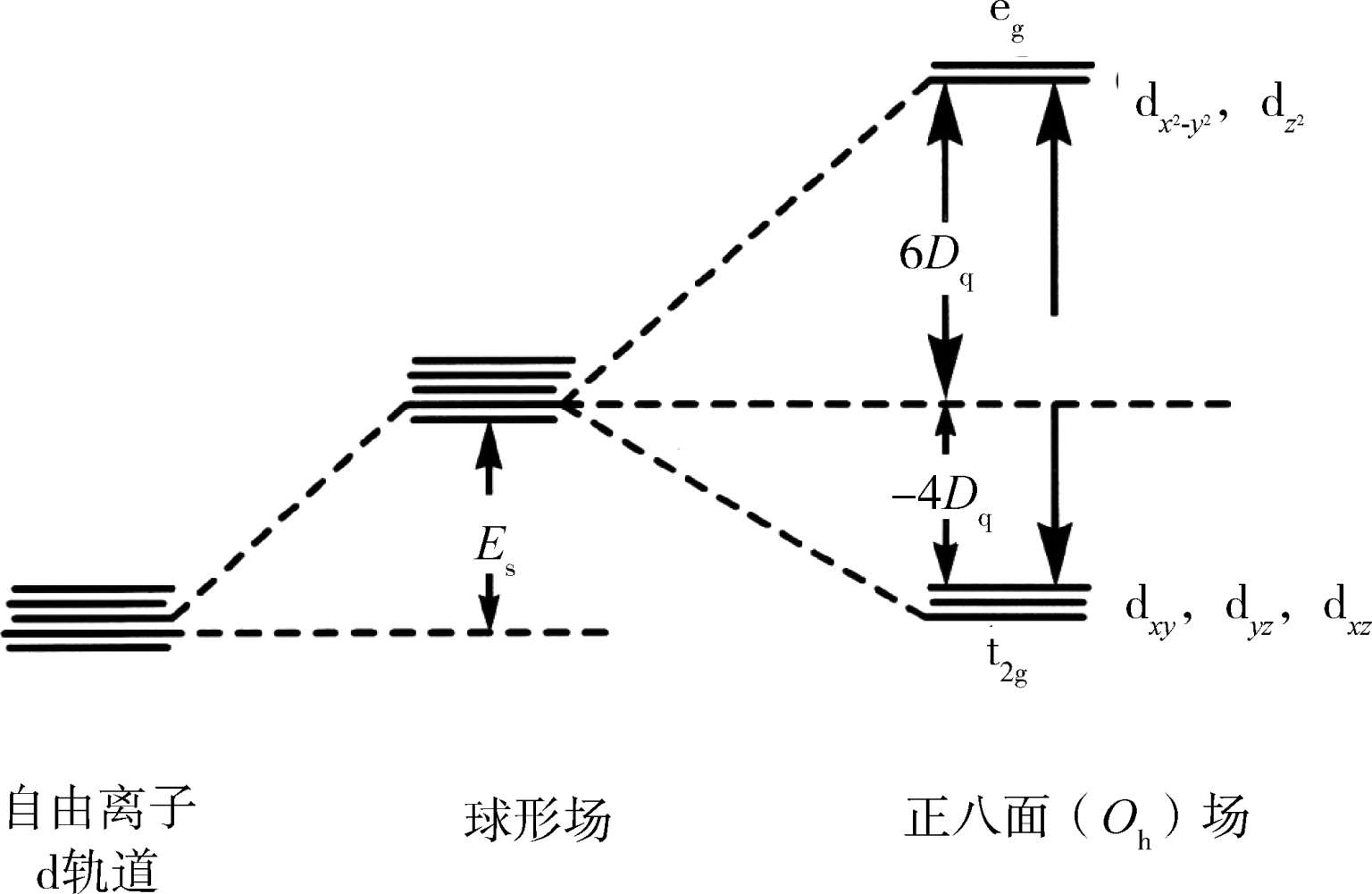
图 2.2 d 轨道在正八面( O h )场中的能级分裂
e
g
和
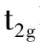 轨道的能量可以根据d轨道在分裂过程中总能量保持不变这一原理来计算。 e
g
两个轨道中可容纳 4 个电子,
轨道的能量可以根据d轨道在分裂过程中总能量保持不变这一原理来计算。 e
g
两个轨道中可容纳 4 个电子,
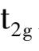 三个轨道中可以容纳 6 个电子,因此, d轨道在分裂后的总能量应为
三个轨道中可以容纳 6 个电子,因此, d轨道在分裂后的总能量应为
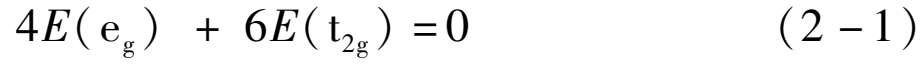
由此可得到:
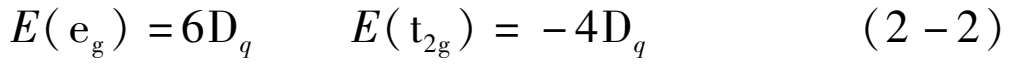
即
E
( e
g
)轨道能量上升了 6
D
q
,而
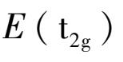 轨道能量下降了 4
D
q
。
轨道能量下降了 4
D
q
。
在固体中激活离子要受到周围其他离子或者配位体的静电场作用,将激活离看作中心离子,而配位体则可看作具有一定极性的恒定外静电场(晶体场),晶体场对电子能级的主要影响是引起其光谱项的分裂。静电场对每个外壳层电子的影响由中心离子与静电场的哈密顿(hamiltonian)所决定。
激活离子能级的能量 E 及其本征波函数 Ψ 通过薛丁谔方程求解:

这里,晶体内具有 N 个电子的激活离子总哈密顿量写作:

式中: H 0 是自由离子哈密顿算符, V f 是晶体场的位能。由于实际上不可能求出多电子离子薛丁谔方程的精确解,所以采用各种近似方法,其中包括微扰理论来求解。微扰理论假设 H 0 的本征函数和本征值是已知的,而将 V f 看作微扰。
自由离子中存在有多种基本相互作用,其中最主要的相互作用是库仑项
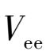 ,它描述电子同核电荷
Z
e
的相互作用和电子间静电排斥的相互作用:
,它描述电子同核电荷
Z
e
的相互作用和电子间静电排斥的相互作用:
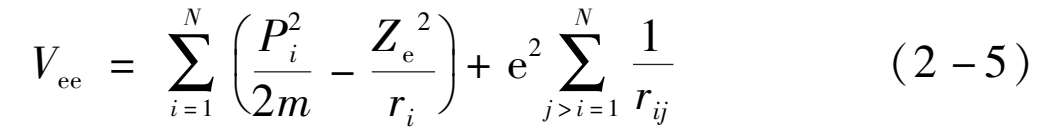
式中: e为电子电荷;
m
是电子质量;
P
i
是电子动量;
r
i
是从核到i电子的径向量;
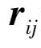 是
j
电子和
i
电子之间的径向量。同一组态的电子在不同状态下的库仑斥力会产生不同的能级,即谱项。
是
j
电子和
i
电子之间的径向量。同一组态的电子在不同状态下的库仑斥力会产生不同的能级,即谱项。
第二个重要的相互作用是电子自旋和轨道耦合作用,即罗素-桑德斯耦合,自旋-轨道相互作用能
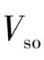 可写作:
可写作:

这里 λ 为自旋-轨道相互作用常数,或称多重态结构系数,它由下式估算

除了自旋-轨道相互作用
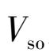 外,还存在磁相互作用,即磁电子静磁场的直接相互作用,但这种相互作用能量约为
外,还存在磁相互作用,即磁电子静磁场的直接相互作用,但这种相互作用能量约为
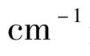 数量级,可予以忽略。同样由于核自旋和核四极矩角动量引起更弱的相互作用也可略而不计,这样晶体内激活离子总哈密顿量可写作:
数量级,可予以忽略。同样由于核自旋和核四极矩角动量引起更弱的相互作用也可略而不计,这样晶体内激活离子总哈密顿量可写作:

由此可得出,晶体场对激活离子能级的影响将取决于
V
f
对
V
ee
和
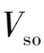 数值之比,它可分成三种情况:弱晶场
数值之比,它可分成三种情况:弱晶场
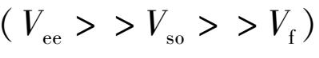 ,中等晶场
,中等晶场
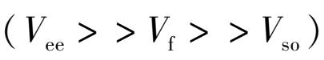 和强晶场
和强晶场
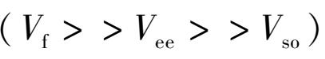 。稀土元素和锕系元素离子属弱晶场情况,其内层被激发的 4f或 5f电子与晶体中周围离子的直接相互作用被5s和5p或6s和6p的外电子层所屏蔽。因此各个晶体的吸收光谱和荧光光谱的特性一般差异不大,并且其斯塔克能级聚集在自由离子能级位置附近。
。稀土元素和锕系元素离子属弱晶场情况,其内层被激发的 4f或 5f电子与晶体中周围离子的直接相互作用被5s和5p或6s和6p的外电子层所屏蔽。因此各个晶体的吸收光谱和荧光光谱的特性一般差异不大,并且其斯塔克能级聚集在自由离子能级位置附近。
在中等晶体场情况下,晶体场通常一级近似地作为对自由离子能级的微扰,而不考虑其自旋-轨道相互作用产生的精细结构,结果斯塔克分裂(Stark split)超过了内多重态分裂,但仍小于相邻多重态间的能隙。一些晶体中的过渡金属离子(具有未充满 3d壳层)具有这种特性。在强晶体场情况下(相应于钯族和铂族离子),斯塔克分裂超出了各多重态间的能隙。
过渡金属离子与晶格振动的相互作用比较强,在光跃迁的过程中可能同时发生晶格振动状态的改变,或者说声子的发射或吸收。因此,吸收和发射光谱的频率就变成
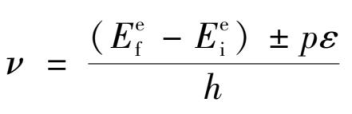 ,这里
ε
代表起作用的声子的能量,
p
代表吸收或发射的声子数,
,这里
ε
代表起作用的声子的能量,
p
代表吸收或发射的声子数,
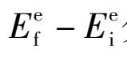 分别表示f态和i态的能量。吸收或发射的声子数不一样,接收到的光频率就不一样。当没有这种晶格振动作用时的频率是
分别表示f态和i态的能量。吸收或发射的声子数不一样,接收到的光频率就不一样。当没有这种晶格振动作用时的频率是
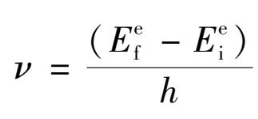 ,这是单一的一条谱线,称为零声子线。有了电声子相互作用时,得到的就是对应于一系列频率不同的谱线。由于热加宽,只有在很低的温度下才能够观察到分立的谱线。在室温下观测到的就是一个比较宽的谱带,这就是所谓声子边带。
,这是单一的一条谱线,称为零声子线。有了电声子相互作用时,得到的就是对应于一系列频率不同的谱线。由于热加宽,只有在很低的温度下才能够观察到分立的谱线。在室温下观测到的就是一个比较宽的谱带,这就是所谓声子边带。
这种与晶格振动耦合比较强系统的光谱可采用所谓位形坐标的方法进行解释。位形坐标可用于解释分立发光中心的光学性质,尤其是与晶格振动相关的光学性质。按照这个模型,要把处于最紧邻配位离子中心的发光中心简化,绝大多数情况下,可以忽略相距较远的其他离子的作用而把发光离子看作孤立中心。在这种情况下,大量的晶格振动模型可以简化为少数的几个简正坐标或具体简正坐标的系统,这些简正坐标就叫作位形坐标。位形坐标模型可以在势能曲线的基础上解释分离中心的发光性质,每一条势能曲线是把发光中心的基态或激发态的总能量作为位形坐标的函数所得出的曲线。这里,总能量是指电子能量和离子能量的总和。
位形坐标模型可以定性地解释诸多现象,如以下几种。
(1)斯托克斯(Stokes)漂移,即在大多数情况下吸收的能量总高于发射的能量,两者之间的能量差就叫作斯托克斯漂移,如图 2.3 所示。
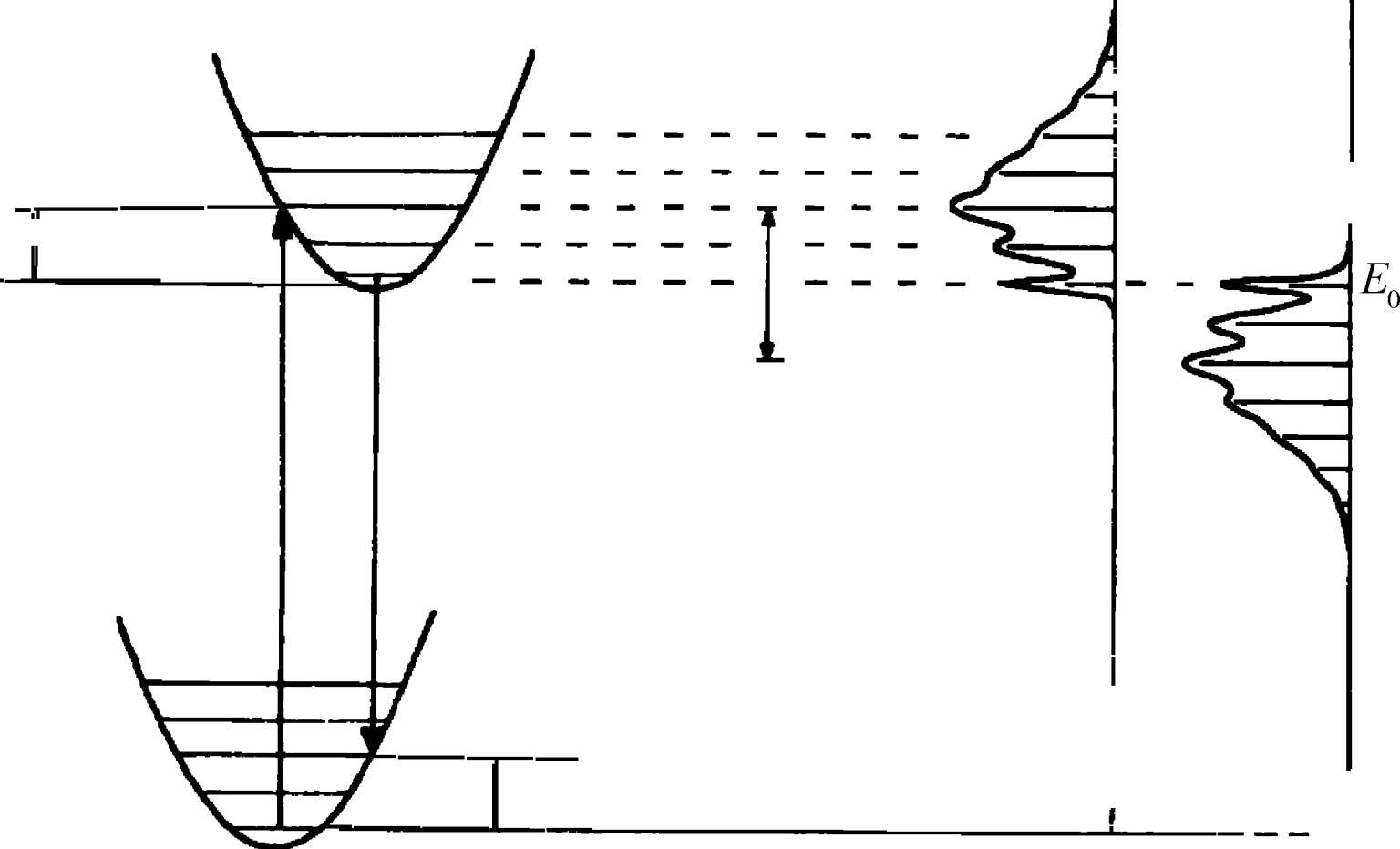
图 2.3 斯托克斯漂移示意图
(2)吸收带和发射带的宽度以及它们的温度依赖关系。图 2.4 所示为发光离子的光学跃迁过程位形坐标模型示意图,假定发光离子和最近邻离子之间的价键作用力可用虎克定律表达,离子相对于平衡位置的偏离可以看作位形坐标(用 Q 表示),基态 U g 的总能量和激发态 U e 的总能量由关系式(2-8)和(2-9)给出:其中, K g 和 K e 是化学键的力常数; Q 0 是基态平衡位置时原子间的距离; U 0 是 Q = Q 0 时的总能量。
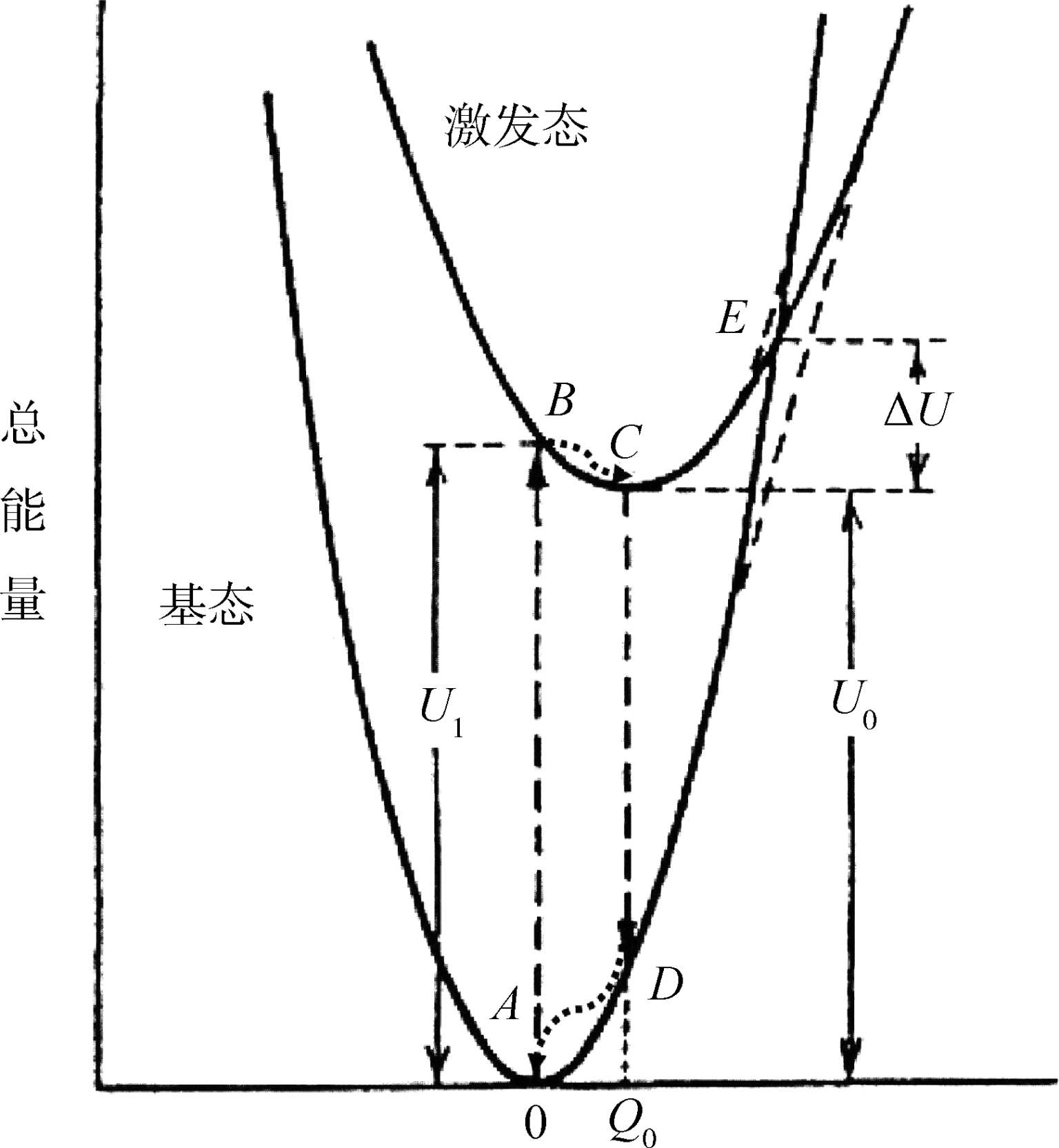
图 2.4位形坐标模型示意图
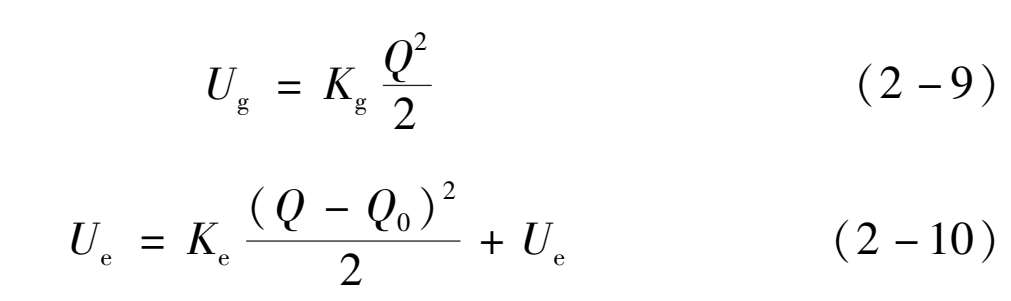
由于基态和激发态之间的电子轨道空间分布不同,引起了电子波函数和近邻离子相互交叠的不同,进一步引起基态和激发态平衡位置和力常数的改变,这就是产生斯托克斯漂移的原因。处于激发态时电子轨道越大,造成电子轨道的能量受位形坐标的影响越小,也就是说,激发态的势能曲线更加平缓。
在图 2.4 中,吸收和发射过程可用竖直的短划线箭头表示,可以认为发光离子核的位置在整个光学过程中保持不变,这就是所谓的Frank- Condon原理。由于原子核要远比电子的重量大10
3
~ 10
5
倍,所以说这种近似是合理的。从基态平衡位置开始的吸收过程用箭头
AB
表示,受激电子由于晶格振动损失能量的几率为
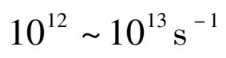
 ,光发射的几率最多为
,光发射的几率最多为
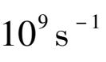 。所以在发光之前,电子从状态
B
弛豫到平衡位置
C
,发光过程为
CD
,弛豫过程是
DA
。一定温度下,电子态在平衡位置附近沿着位形坐标曲线振动,可达到热能kT。振动的幅度就形成了吸收和发射跃迁的宽度。
。所以在发光之前,电子从状态
B
弛豫到平衡位置
C
,发光过程为
CD
,弛豫过程是
DA
。一定温度下,电子态在平衡位置附近沿着位形坐标曲线振动,可达到热能kT。振动的幅度就形成了吸收和发射跃迁的宽度。
当两个位形坐标曲线相互交叉时,激发态的电子可以在热能的作用下通过交点 E 无辐射地到达基态,如图 2.4 所示。也就是说,若假定非辐射弛豫过程具有激活能ΔU,单位时间内的跃迁几率 N 可由下表示:
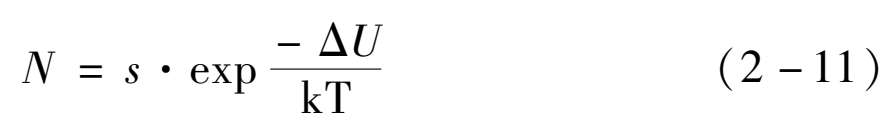
其中,
s
是基态和激发态之间跃迁几率和从激发态到达交点
E
的频率的乘积,
s
可以看作一个常数,由于温度对它的影响很弱,故可把它叫作频率因子,其典型的数量级为
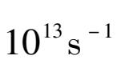 。
。
利用方程(2-11),用 W 表示荧光几率,荧光效率 η 可表示为
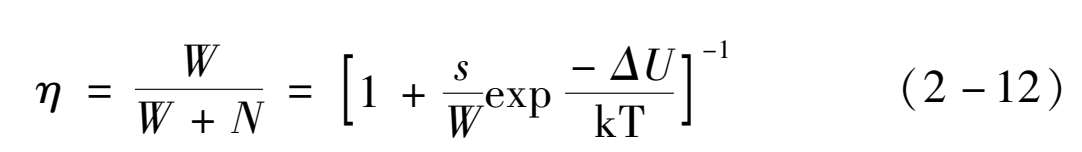
如果激发态 C 的平衡位置处于基态位形坐标曲线的外面,激发态和基态相交而使电子从 B 弛豫到 C ,产生无辐射跃迁过程。
因为基态和激发态的离子的位置不同,故位形坐标的差( Q 0 -Q′ 0 )可以用来衡量电-声子耦合作用的大小。电子-声子相互作用能,也就是晶格弛豫能为
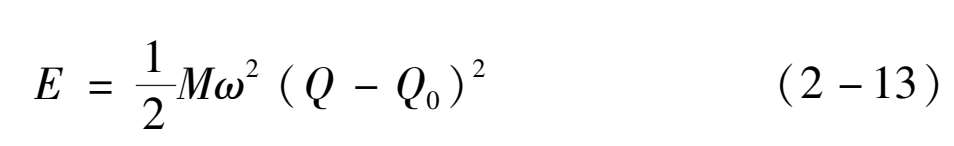
其中, M 是离子的质量;ω是晶格振动频率。
晶格弛豫能所折合的声子数为
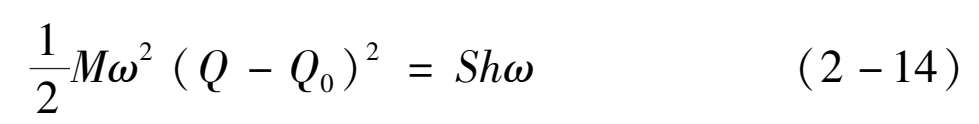
其中, S 叫作黄昆-里斯因子,表示两个电子能级对基质环境的敏感不同,衡量电子-声子耦合作用的程度。