




过渡金属是指元素周期表中第四周期的一组元素,在离子固体中这些元素失去最外壳层 4s电子和部分 3d电子形成离子键,它们的电子组态为

例如:过渡金属Cr有 24 个电子,当它作为三价离子掺入固体中时,它失去外层 3 个电子形成离子键,它的电子组态为

过渡金属离子具有不完全 3d外壳层和可以进行相互间光学跃迁的低位能级。由于 3d轨道的电子的屏蔽,过渡金属离子与基质晶体的离子之间存在相互作用。在晶体中过渡金属离子的光谱展现出纯电子的锐跃迁和电子-声子耦合的宽带发射,后者可能产生宽调谐激光。显然静电场对晶体中的离子作用是很重要的,静态晶体场通常用点电荷模式来近似模拟,由点电荷表示的配位离子的静电场和配体离子假定固定在平均晶格位置。配位离子的几何排列反映了离子的结晶环境的对称性,导致了电子能级的分类。
图 2.6 所示为特定对称的静电晶体场的三种离子排列。过渡金属离子在离子晶体中倾向于占据近八面体对称的位置,在完全八面体对称( O h )中,中心阳离子位于六个等距负离子的中心,从原点沿± x , . y , . z 正交轴每个负电荷(. Z e )的距离为 a 。在四面体对称( T d )中阳离子置于四面体中心,四个负离子放置在正四面体的顶点上。当八个负离子放置在一个正立方体的角上,而阳离子置于立方体中心时,这种晶体场被称为立方对称。过渡金属离子最常见的多面体排列是六配位,它所占据的晶场具有八面体对称性,而实际上八面体场总有微小畸变。如果沿着立方体对角线的伸长或压缩就会畸变成三方对称,如图 2.7 所示。如果沿着(001)方向拉伸或压缩也会发生畸变成四方对称,如图 2.8 所示。更复杂的畸变会导致更低的对称性。但是,在晶体场中八面体晶体场分量最强,其他低对称性场分量比较弱。

图 2.6 不同对称性的静电晶体场的离子排列

图 2.7 三方畸变的八面体晶场

图 2.8 四方畸变的八面体晶场
在多电子体系中除了配位场的作用外,还存在着 N 个d电子间的相互作用。在这两种作用中,如果配位场的作用较大而电子相互作用较小,则称之为强晶体场。反之,若配位场的作用小于电子相互作用,则称之为弱晶体场。过渡金属离子在介质中所受到的晶场作用可视为是对自由离子的微扰,配位场的静电场对过渡金属离子外壳层电子的影响由中心离子和静电场的哈密顿量决定。过渡金属的电子能量本征函数 E 通过薛定鄂( Schrödinger)方程 Ψ 求解:

晶格离子中电子的总哈密顿(Hamiltonian)量:

其中, H eN 是电子与原子核相互作用的哈密顿量; H ee 是电子与电子相互作用哈密顿量; H so 是电子的自旋与轨道相互作用的哈密顿量; H c 为晶场哈密顿量; H ext 为外场作用的哈密顿量。晶体场对激活离子能级的影响将取决于 H c 对 H ee 和 H so 数值之比,它可分成三种情况。
1)弱晶场

2)中晶场

3)强晶场

稀土元素和锕系元素离子属弱晶场情况,其内层被激发的 4f或 5f电子与晶体中周围离子的直接相互作用被 5 -或 6-s,- p,- d外电子层所屏蔽。因此各个晶体的吸收光谱和荧光光谱的特性一般差异不大,并且其斯塔克能级聚集在自由离子能级位置附近。在中等晶体场情况下,晶体场通常一级近似地作为对自由离子能级的微扰,而不考虑其自旋-轨道相互作用产生的精细结构,结果斯塔克分裂超过了内多重态分裂,但仍小于相邻多重态间的能隙。在强晶体场情况下(相应于钯族和铂族离子),斯塔克分裂超出了各多重态间的能隙。
晶体中的过渡金属离子的 3d n 电子处于外壳层,它们对晶体环境的影响非常敏感,其晶格离子的作用能和电子与电子之间的库仑相互作用能同属一个数量级(大约 10 4 cm - 1 ),远大于其自旋-轨道作用能(约 10 2 cm - 1 )。因此过渡金属离子的能级易受晶格离子包括晶格场和晶格振动两方面的影响,其能级结构随基质的不同而有很大的差别。
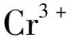 能级
能级
由于 3d电子之间的库仑相互作用,对于八面体晶场的
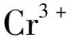 的能级的评估比Ti
3+
更为复杂。库仑相互作用的特征在于拉卡参数
B
和
C
,库仑相互作用使电子进入
2
的能级的评估比Ti
3+
更为复杂。库仑相互作用的特征在于拉卡参数
B
和
C
,库仑相互作用使电子进入
2
 光谱项,库仑相互作用负责这些状态的能量分离。
4
F态是自由离子
光谱项,库仑相互作用负责这些状态的能量分离。
4
F态是自由离子
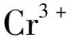 的最低态基谱项,根据洪德的规则,接着高能级谱项是
4
P和
2
G。在八面体晶体场中,
4
F谱项分裂成
的最低态基谱项,根据洪德的规则,接着高能级谱项是
4
P和
2
G。在八面体晶体场中,
4
F谱项分裂成
 三个能级,
4
P谱项成为
4
T
1
能级,
2
G谱项分裂成
三个能级,
4
P谱项成为
4
T
1
能级,
2
G谱项分裂成
 四个能级。拉卡参数
B
和
C
表征库仑相互作用的强度。
B
和
C
的值随离子和基质的不同而不同,通常由光谱数据来确定。对于自由离子
四个能级。拉卡参数
B
和
C
表征库仑相互作用的强度。
B
和
C
的值随离子和基质的不同而不同,通常由光谱数据来确定。对于自由离子
 ,
B
= 920
,
B
= 920
 C
=3 68.
C
=3 68.
 ,
C/
B
比率γ几乎与原子数和电子数无关。所有过渡金属离子的γ值都在 4.2 .4.9 的范围内。因此,不同能级之间的能量分离仅取决于两个参数
B
和
D
q
。
,
C/
B
比率γ几乎与原子数和电子数无关。所有过渡金属离子的γ值都在 4.2 .4.9 的范围内。因此,不同能级之间的能量分离仅取决于两个参数
B
和
D
q
。
1954 年Y.Tanabe和S.Sugano应用强场方法,计算了八面体中全部 3d
n
体系各个能级的能量,将各状态的能量作为分裂能10
D
q
和电子相互作用参数
B
、
C
的函数,考虑到配合物中
B
和
C
的值可能与自由离子中的不同,故在能量方程中两端均用
B
除之,即能量以
B
为单位,能量参数则减少为
D
q
/
B
和
C/
B
两个。假定
C/
B
在配合物中与在自由离子中相同,以
E/
B
对 10
D
q
/
B
作图得到所谓的Tanabe- Sugano能级图。这些能级以八面体
O
h
群不可约表示
 形式来标记。假定
4
A
2
能级为零能量能级,其他能级能量依此进行测量。研究光谱时最关心的是自旋多重度相同的状态之间的能量间隔,而这种能量间隔只是
B
的函数,与
C
无关,所以Tanabe- Sugano图对同一组态的离子具有普遍意义,图2.9 为
形式来标记。假定
4
A
2
能级为零能量能级,其他能级能量依此进行测量。研究光谱时最关心的是自旋多重度相同的状态之间的能量间隔,而这种能量间隔只是
B
的函数,与
C
无关,所以Tanabe- Sugano图对同一组态的离子具有普遍意义,图2.9 为
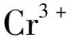 的 3d
3
组态Tanabe - Sugano能级图。
的 3d
3
组态Tanabe - Sugano能级图。

图 2.93d 3 组态离子的Tanabe - Sugano能级图
在晶体场中完美的八面体对称位点难得发现,最常见都是与完美八面体对称性若有偏差的畸变,这微小畸变会产生约化对称点,例如三方(D
3
)、四方(D
4
)和正交(D
2
)。在晶场中由于优势晶场分量为八面体,而畸变分量较小,因此按照八面体对称对光谱的总体特征进行分类。以
 掺杂材料中由畸变对称性降低到三方晶体场的常见现象为例,三方畸变分裂基态
2
T
2
成
2
E和
2
A
1
两个能级。相反,激发态
2
E移动,但不在三方场位置分裂。然而自旋-轨道耦合允许三方畸变分裂激发态
2
E和最低态
2
E两者分裂成 2
掺杂材料中由畸变对称性降低到三方晶体场的常见现象为例,三方畸变分裂基态
2
T
2
成
2
E和
2
A
1
两个能级。相反,激发态
2
E移动,但不在三方场位置分裂。然而自旋-轨道耦合允许三方畸变分裂激发态
2
E和最低态
2
E两者分裂成 2
 和
和
 两个能级。上能级
2
E由于受Jahn- Teller效应影响进一步分裂,如图 2.10 所示。
两个能级。上能级
2
E由于受Jahn- Teller效应影响进一步分裂,如图 2.10 所示。

图 2.10 三方晶体场、自旋-轨道耦合和Jahn - Teller作用下3d 1 组态的能级分裂
对于
 ,三方畸变和自旋-轨道耦合都不能单独将基态
,三方畸变和自旋-轨道耦合都不能单独将基态
 分裂。然而,在三方畸变和自旋-轨道耦合的共同作用下基态
分裂。然而,在三方畸变和自旋-轨道耦合的共同作用下基态
 分裂成 2
分裂成 2
 和
和
 两个能级。在电子自旋共振(ESR)谱学中,这种分裂被称为零场分裂。与此相类似,在三方晶场和自旋-轨道 耦合的作用下第一激发态
2
E分裂成 2
两个能级。在电子自旋共振(ESR)谱学中,这种分裂被称为零场分裂。与此相类似,在三方晶场和自旋-轨道 耦合的作用下第一激发态
2
E分裂成 2
 和
和
 两个能级。
2
E能级分裂可以通过激发光谱和荧光光谱来测量。与
两个能级。
2
E能级分裂可以通过激发光谱和荧光光谱来测量。与
 和
2
E能级不同,无论三方畸变还是自旋-轨道耦合都可以将第二激发态
和
2
E能级不同,无论三方畸变还是自旋-轨道耦合都可以将第二激发态
 分裂。例如,在自旋-轨道耦合的作用下将
分裂。例如,在自旋-轨道耦合的作用下将
 能级分裂成
能级分裂成
 、
、
 和
和
 能级,在三方畸变和自旋-轨道耦合的共同作用下将
能级,在三方畸变和自旋-轨道耦合的共同作用下将
 能级分裂成六个能级,如图 2.11 所示。
能级分裂成六个能级,如图 2.11 所示。

图 2.11 三方晶场和自旋-轨道耦合作用下八面体场中能级分裂