在配位场作用下,自由离子的简并的五个d轨道要发生能级分裂,例如在八面体场中分裂成两组,一组是能量较高的e
g
轨道
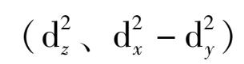 ,另一组是能级较低的t
2
g轨道
,另一组是能级较低的t
2
g轨道
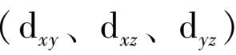 ,两组轨道之间的能量差称为分裂能Δ
0
。当这些轨道没有全被电子充满时,电子可以在两组轨道之间进行跃迁,这种跃迁产生的光谱就称为配位场光谱,或称为d .d光谱。
,两组轨道之间的能量差称为分裂能Δ
0
。当这些轨道没有全被电子充满时,电子可以在两组轨道之间进行跃迁,这种跃迁产生的光谱就称为配位场光谱,或称为d .d光谱。
在自由原子或离子中,电子排布是按泡利原理和能量最低原理填充在原子轨道上的。原子或离子把其所有的电子填充在给定的原子轨道上的排布方式称为电子组态。如
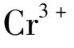 离子的电子组态为 1s
2
2s
2
2p
6
3s
2
3p
6
3d
3
,其中内层轨道已被电子填满,称为闭壳层。对于闭壳层,由于轨道已全部被电子填满,其电子排布方式只有一种,但对于未填满电子的轨道,电子的排布方式则有很多种,每一种排布方式都反映了这个组态的一个微观状态,称为微组态。
离子的电子组态为 1s
2
2s
2
2p
6
3s
2
3p
6
3d
3
,其中内层轨道已被电子填满,称为闭壳层。对于闭壳层,由于轨道已全部被电子填满,其电子排布方式只有一种,但对于未填满电子的轨道,电子的排布方式则有很多种,每一种排布方式都反映了这个组态的一个微观状态,称为微组态。
同一组态的电子(不考虑电子间相互作用)能级是相同的,即简并的。对于同一电子组态可以存在有许多不同的微观状态,在不同的微观状态中,电子之间的相互作用不一定相同,因此同一电子组态,若考虑电子间相互作用,往往存在多个能级。
当考虑电子间的静电排斥作用时,显然排布方式不同,电子之间排斥就不同。在物理学中,同一电子组态中的电子由于考虑其电子排斥作用,而引起原来的简并轨道分裂成能级不同的若干种状态,把这种分裂后的能级叫光谱项,通常用
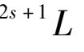 表示,其中
L
是总的轨道角动量量子数,
S
是总自旋量子数,2
S
+ 1 称为谱项多重度。当
L
= 0,1,2,3,4,5,6,7,8,…时分别用S, P,D, F, G, H, I, K, L, …表示。由于单电子的轨道角动量属于向量范畴,因此,多电子体系的总轨道角动量
L
是通过单电子轨道角动量l的向量加和而成,即
表示,其中
L
是总的轨道角动量量子数,
S
是总自旋量子数,2
S
+ 1 称为谱项多重度。当
L
= 0,1,2,3,4,5,6,7,8,…时分别用S, P,D, F, G, H, I, K, L, …表示。由于单电子的轨道角动量属于向量范畴,因此,多电子体系的总轨道角动量
L
是通过单电子轨道角动量l的向量加和而成,即
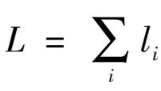 (
l
i
是第
i
个电子的角动量)。
L
与总轨道角动量量子数有下式关系
(
l
i
是第
i
个电子的角动量)。
L
与总轨道角动量量子数有下式关系
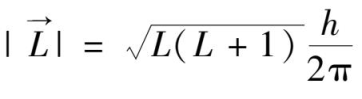 ,
L
是总轨道角动量量子数。
,
L
是总轨道角动量量子数。
与此类似,总自旋角动量为
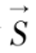 =
=
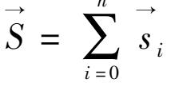 (
s
i
是第
i
个电子的自旋角动量,
n
为电子的个数),且
(
s
i
是第
i
个电子的自旋角动量,
n
为电子的个数),且
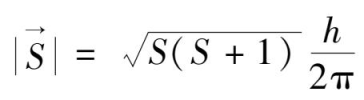 (
S
等于零,正整数或半整数).
S
为总的自旋角动量量子数,它的数值等于
(
S
等于零,正整数或半整数).
S
为总的自旋角动量量子数,它的数值等于
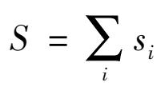 (
s
为单个电子的自旋量子数,等于+ 1 /2 或-1 /2)。
(
s
为单个电子的自旋量子数,等于+ 1 /2 或-1 /2)。
在考虑电子之间相互作用后,计算表明体系能量仅与 L , S 有关, L , S 相同,能量就相同,同一谱项可有(2 L + 1)(2 S + 1)个能量相同的状态。如 3d 2 组态,可分裂出多个谱项。在这些谱项中能量最低的谱项称为基谱项。严格来说,谱项具体能量数值应该经过微扰计算与光谱数据来确定,然后根据数值决定其高低,但定性上可根据洪特第一法则来确定基谱项,即“同一组态的谱项中, S 最大者能级最低,当 S 相同,则 L 最大者能级最低”。例如,3d 2 组态的五个光谱项中 3 F为基谱项。
如果除了考虑自由原子或离子中电子的排斥作用外,还考虑轨道角动量和自旋角动量之间的作用耦合时,从总轨道角动量
L
和总自旋角动量
S
的耦合,可得总角动量
J
,即
J
=
L
+
S
,
J
叫总角动量量子数,其数值处于|
L
+
S
|和|
L
-
S
|之间。也就是说,考虑轨道与自旋相互作用时,同一光谱项又会分裂成不同
J
值的能级,这些能级叫作光谱支项,用
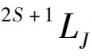 表示。例如 3d
2
组态中基谱项
3
F,若考虑轨道-自旋耦合时,由于
L
= 3.
S
= 1,故
J
= 4,3,2。因此,
3
F可分裂为三个光谱支项:
3
表示。例如 3d
2
组态中基谱项
3
F,若考虑轨道-自旋耦合时,由于
L
= 3.
S
= 1,故
J
= 4,3,2。因此,
3
F可分裂为三个光谱支项:
3
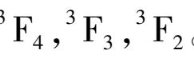 一般说来,光谱支项之间能级差比光谱项之间能级差小得多。在同一光谱项中能级最低的光谱支项叫光谱支项的基谱项。根据洪特第二法则:对于给定的组态、多重性和轨道角动量,若组态的电子填充轨道上未达到电子最大容纳数的一半时,
J
= .
L
-
S
|的光谱支项能级最低,超过半数时,
J
= .
L
-
S
|的能级最低。
一般说来,光谱支项之间能级差比光谱项之间能级差小得多。在同一光谱项中能级最低的光谱支项叫光谱支项的基谱项。根据洪特第二法则:对于给定的组态、多重性和轨道角动量,若组态的电子填充轨道上未达到电子最大容纳数的一半时,
J
= .
L
-
S
|的光谱支项能级最低,超过半数时,
J
= .
L
-
S
|的能级最低。
对于每个光谱支项,可有(2 J + 1)个不同的状态,在无外磁场作用时,它是简并的,只有在外磁场作用下,才又会分裂。3d 2 组态能级分裂情况,如图 2.5 所示。
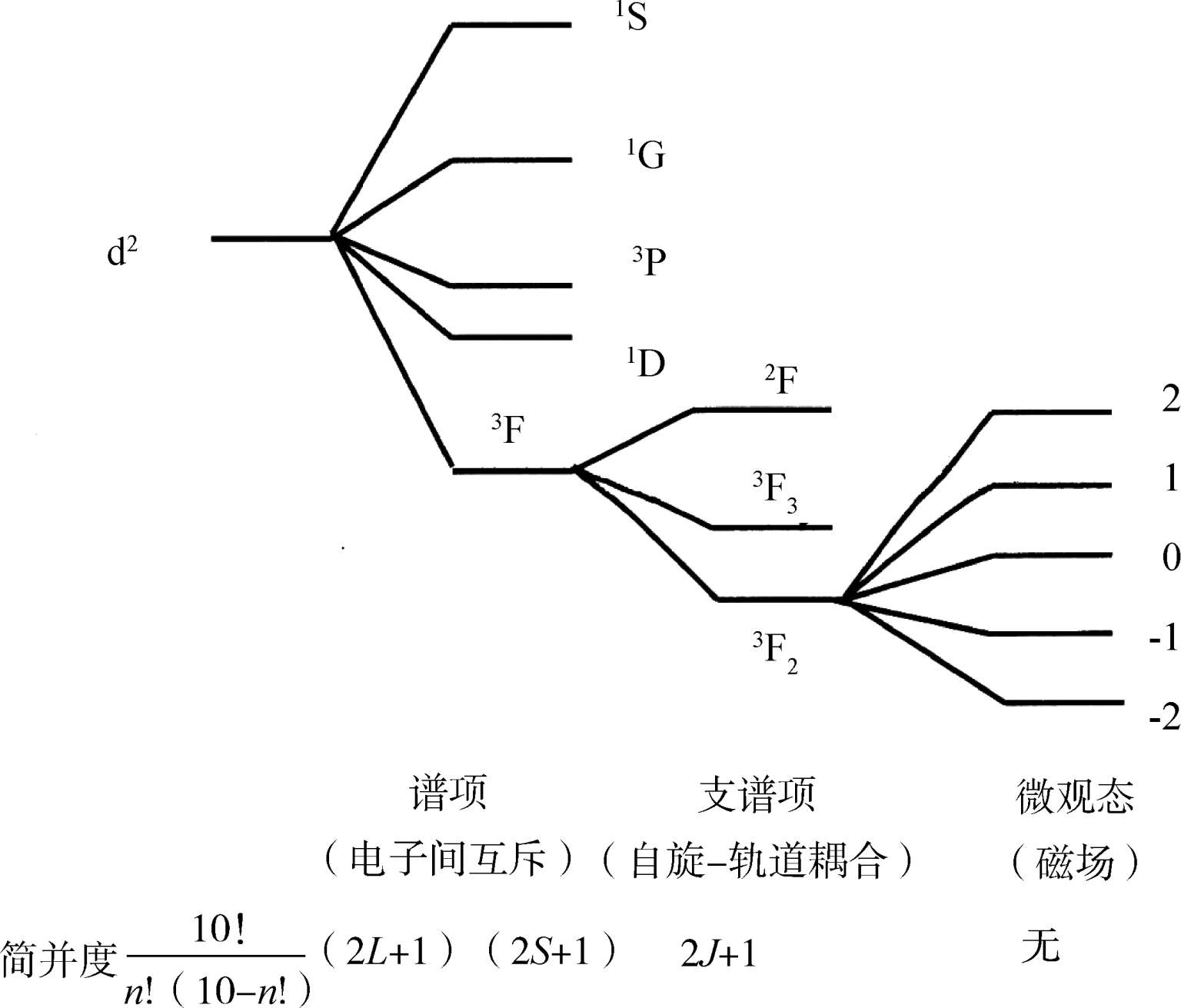
图 2.5 3d 2 组态能级分裂示意图
金属离子同配位离子形成化合物时,中心离子就要受配位体电场的作用,因而它的电子状态就要发生变化,即自由离子的光谱项在配位体电场的作用下,要发生进一步分裂,分裂后产生的新能级称为配位场谱项。
对于多电子体系,根据中心离子电子间的相互作用及配位场场强的相对大小可有两种推求配位场谱项的方案。
1)弱场处理方案
如果体系中电子间的相互排斥作用对能量的贡献远大于配位场的作用,则采用所谓弱场处理方法,即首先考虑中心原子或离子中电子之间的相互作用,先得到光谱项,然后再考虑配位体场对自由离子光谱项的作用而产生配位场谱项
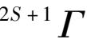 。在采用弱场方法处理时,又分两种情况,一种是配位场作用比电子间相互作用和自旋-轨道耦合作用都小,则先考虑电子间的作用得出光谱项,再考虑自旋-轨道耦合分裂出光谱支项,最后再考虑配位场的作用得出配位场谱项;另一种情况是配位场作用小于电子间的相互作用而大于自旋-轨道耦合作用,此时可先考虑电子间的相互作用得到自由离子光谱项,然后考虑配位场作用得到配位场谱项,再考虑自旋-轨道耦合作用得出配位场光谱支项。这两种情况推导结果相同,采用哪种程序要由这些作用的相对大小确定,至于配位场谱项能级相对高低,群论方法解决不了,只有通过量子化学计算确定。
。在采用弱场方法处理时,又分两种情况,一种是配位场作用比电子间相互作用和自旋-轨道耦合作用都小,则先考虑电子间的作用得出光谱项,再考虑自旋-轨道耦合分裂出光谱支项,最后再考虑配位场的作用得出配位场谱项;另一种情况是配位场作用小于电子间的相互作用而大于自旋-轨道耦合作用,此时可先考虑电子间的相互作用得到自由离子光谱项,然后考虑配位场作用得到配位场谱项,再考虑自旋-轨道耦合作用得出配位场光谱支项。这两种情况推导结果相同,采用哪种程序要由这些作用的相对大小确定,至于配位场谱项能级相对高低,群论方法解决不了,只有通过量子化学计算确定。
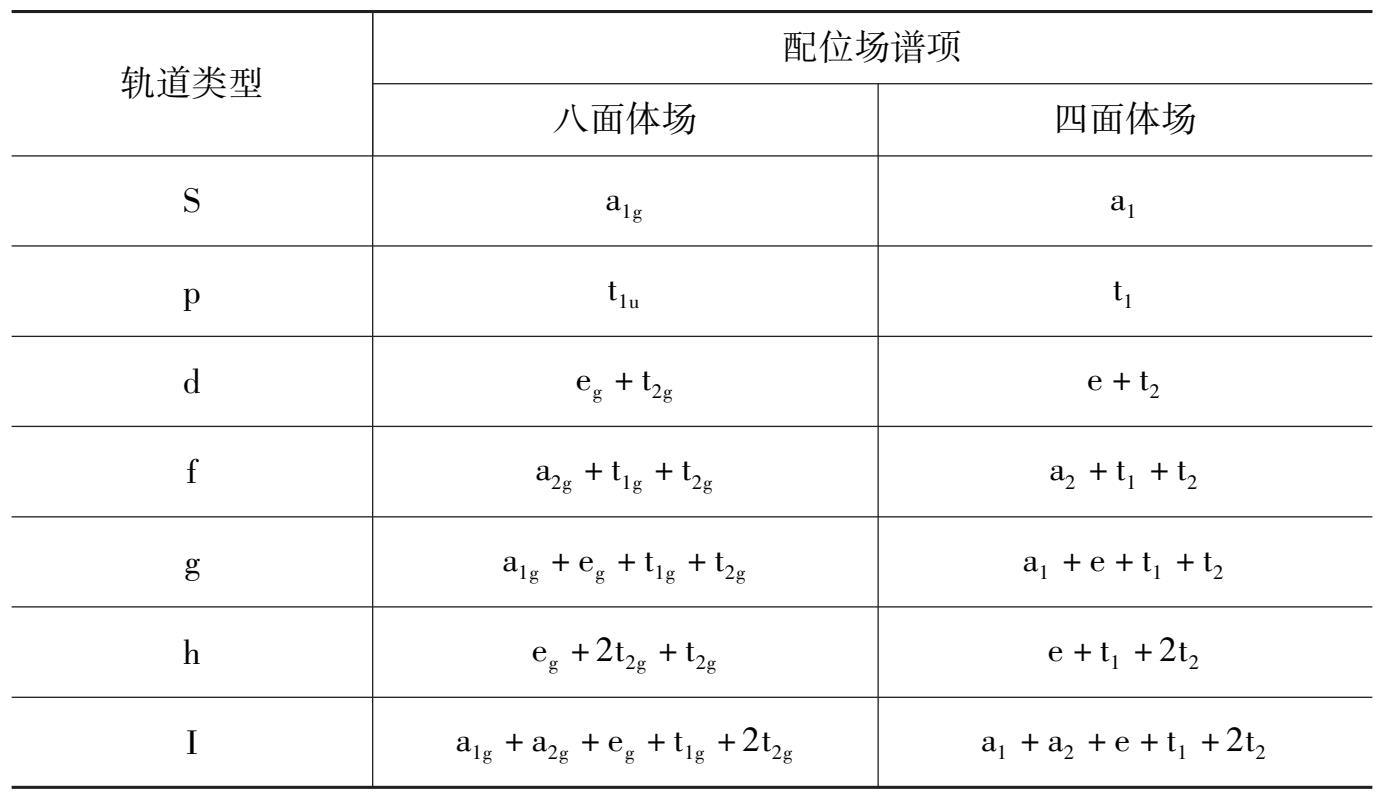
根据光谱项写出配位场谱项的方法如下:由于多电子原子的 L 值与单电子原子 l 值具有相同的简并度,即(2 L + 1)=(2 l + 1),所以光谱项在配位场作用下的分裂与单电子能级在配位场中的分裂相似。因此根据单电子原子轨道的能级分裂可以直接写出配位场谱项。表 2 -1 列出了八面体场和四面体场中各轨道分裂情况。
由于在弱场极限情况下,配位场作用不足以改变电子自旋状态,或者说忽略了配位场对电子自旋的作用。因此在配位场作用下,由某个光谱项分裂所得到的配位场谱项都具有与原光谱项相同的自旋多重度。
2)强场处理方案
如果配位场和中心离子的作用对能量的贡献大于金属离子内部电子之间的相互作用,则首先考虑配位场对d电子轨道的排斥作用而引起的能级分裂,得到配位场组态,然后再考虑金属离子中电子之间的相互作用而得到配位场谱项。这种处理方法被称为强场处理方案。
表 2 -1 单电子原子轨道在配位场作用下的能级分裂