




爱因斯坦(1879. 5. 14—1955. 4. 18)是举世闻名的伟大科学家。他智慧而又幽默。一年暑假来临之际,学生们询问爱因斯坦新近在学术上是否有新发现。他非常神秘地说:“最近我真的有一个发现:两点之间的距离是什么?就是暑假的开端到暑假的结束。”在学生们的欢声中,他亲切地说:“祝诸位度个愉快的暑假。”
爱因斯坦成名后,仍继续为《法兰克福报》写稿。下面是他提出的一道题:图中几个圆的圆心是4 个小等腰三角形与3 个大等腰三角形的顶点,把数字1 ~9 填入圆内,使每个三角形顶点的数字和都相等。(图 68)
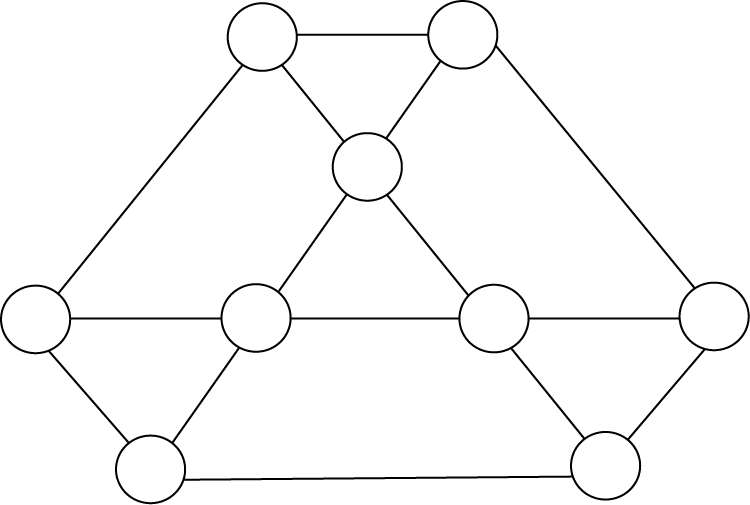
图 68
一些数按着一定的规则,被填在特定形状的图形里。我们称这种图形为数阵(图)。待等到我们学习研究一番之后,有了“破译”它们的规则之奥秘的真功,爱因斯坦做过的题,我们就能在笑谈之中破解了。
【例 1】
把 1、2、3、4、5、6、7 分别填入图中各〇内,使每条线段上的三数之和相等。(图 69)
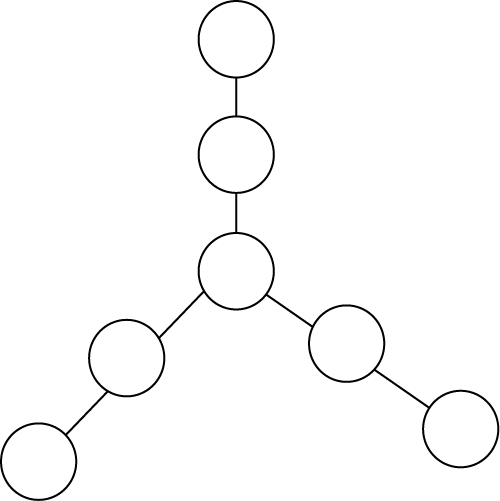
图 68
想一想
中心〇内的数是重复使用在三条线段上的,其余 6 个〇内的数都只使用一次。只要上、左、右各一对数的和相等,则三条线段上的三数之和也就相等了。请看(图 70)
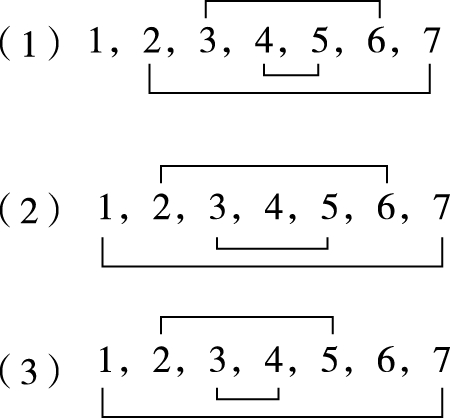
图 70
做一做
有如下三个基本解:(图 71)
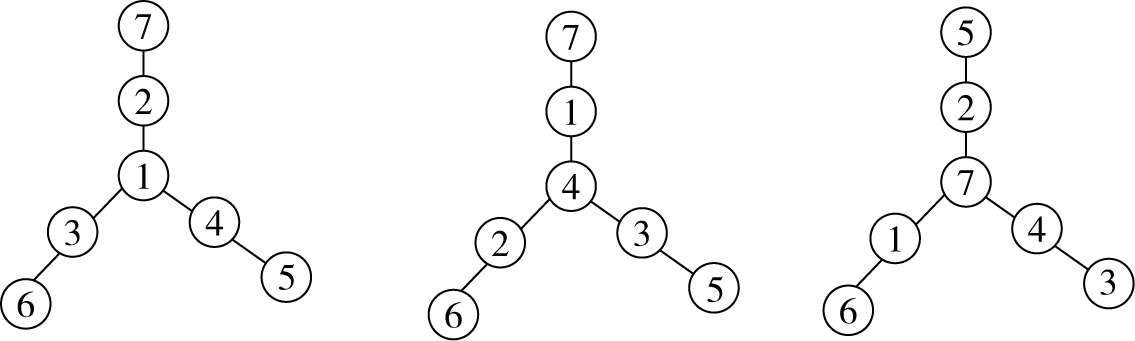
图 71
理一理
也可以这样来找定中心数 1、4、7:
1+2+3+4+5+6+7=28=8×3+4
中心数一定,就全盘皆活了。
【例 2】
把 1、2、3、4、5、6 分别填入图中各小圆内,使每个大圆上四数之和都是 16。(图 72)
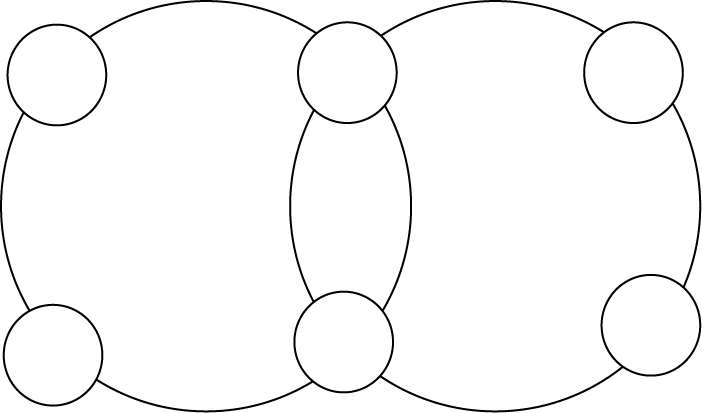
图 72
想一想
1+2+3+4+5+6=21,可大圆上四数之和为 16,两个大圆上共有 16×2-32,比21 多出11 了。从哪儿多出来的?噢,是中间两个小圆内的数在两个大圆里都被计数(重复使用)了,可见 11 必为 5、6 之和。
做一做
如图(图 73)
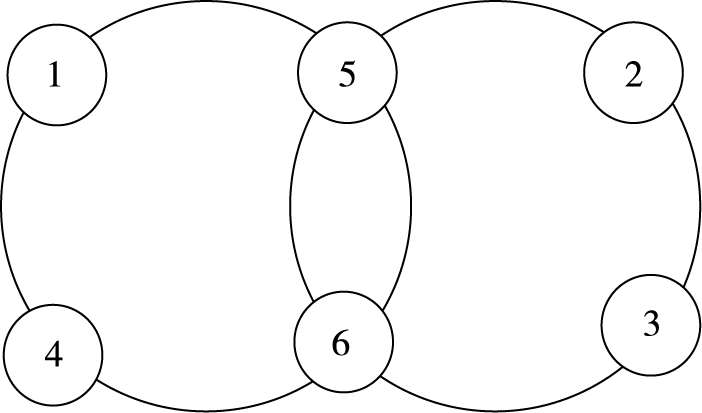
图 73
理一理
在数阵图上“走走线”,找出重复使用的数(的和),确定交点上应该填什么,这是“破阵”的关键。
【例 3】
把1、2、3、4、5、6 分别填入图中各○内,使三角形每边上三数之和都相等。(图74)
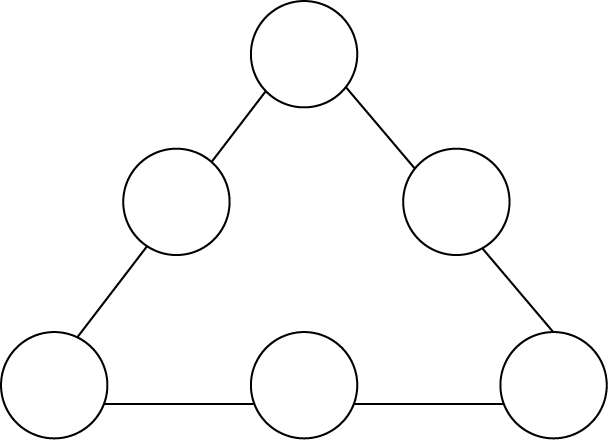
图 74
想一想
三角形三个顶点上的数是重复使用的,三个顶点至少填 1、2、3(此时每边三数和为[(1 +2 +…+6)+(1 +2 +3)]÷3=9),至多填 4、5、6,(此时每边三数和为[(1 +2 +…+6)+(4 +5 +6)]÷3=12)。看来每边三数和有 9、10、11、12 四种情形。
做一做
有四个基本解如下:(图 75)

图 75
理一理
以每边三数和是 10 为例,当然这样来确定三个顶点填啥数:10× 3-(1+ 2+…+ 6)=9=1+3+5。这里之所以取 1、3、5,而不用 1、2、6 等,那是考虑顶点三数与边中三数的“匹配”。
【例 4】
把1 ~8 八个自然数填入图中各口内,使每一横行、竖行的三数之和相等。(图76)

图 76
想一想
各行三数之和相等,那么三个“三数之和”的和必为 3 的倍数。十字中心口内的数是重复使用的,设它为a。有 1+2 +…+ 8+a=36+a,要让 36+a是 3 的倍数,这里只有取a=3 或 6。
做一做
有每行和为 13、14 两个基本解:(图 77)

图 77
理一理
充分利用重复计算的位置的信息,常常是数阵解码的突破口所在。给这个重复位置一个未知数代码,再利用倍数关系“解码”,是我们常用的方法。
【例 5】
把 1、2、4、6 分别填入图中各空白区域内,使每个圆内四数之和都是 15。(图78)
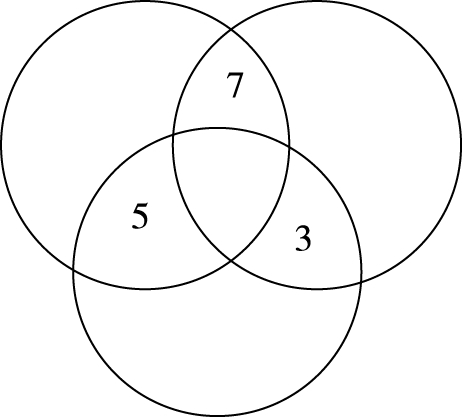
图 78
想一想
这里 3、5、7 使用了两次(多用一次),中心区域内的数使用了三次(多用两次),其余三数备用一次。用上例“设码解码”的办法可求得中心区域内数a:(1+2 +…+ 7)+(3+5+7)+ 2a=15×3,解得a=1。
做一做
如右图。(图 79)
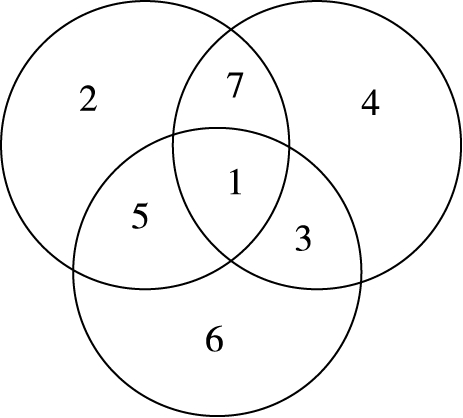
图 79
理一理
利用数的奇偶性破阵,更为简明。和 15 是奇数,待填四数中只有 1 是奇数,而每个圆内已填的两数和均为偶数,可见中心区域内必定填 1。
【例 6】
把 1 ~8 八个自然数填入正方形上的各○内,使每边上三数之和相等。(图80)
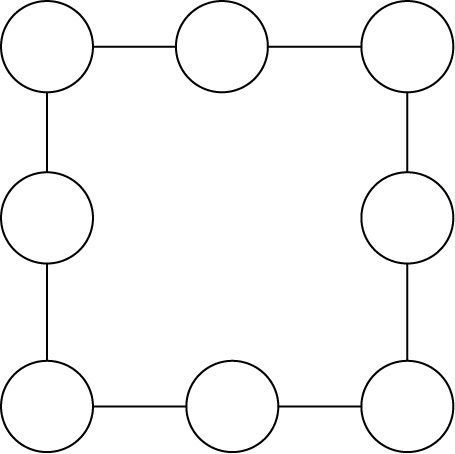
图 80
想一想
四条边上相等的“三数和”的和必定是 4 的倍数;所给八数和 36 是 4 的倍数。可见,各多使用了一次的四顶点上的数,(1)至少要取 1、2、3、6(它们的和 12 是 4的倍数),此时每边三数和为(36+12)÷ 4=12;(2)至多取 3、6、7、8(它们的和 24是 4 的倍数),此时每边三数和为(36+24)÷ 4=15。由(1)、(2)可知,本例至少有每边和为 12、13、14、15 的四个基本解。
当每边三数和为 13,分拆 13 成三数:
这样,找到了四顶点上的数为 1、2、5、8(其和是 4 的倍数),只是在填数时要注意 8 与 5 不能填在同一边(因为 8 +5=13)。当然,还可以作别样分拆。
做一做
选列四个基本解如下:(图 81)
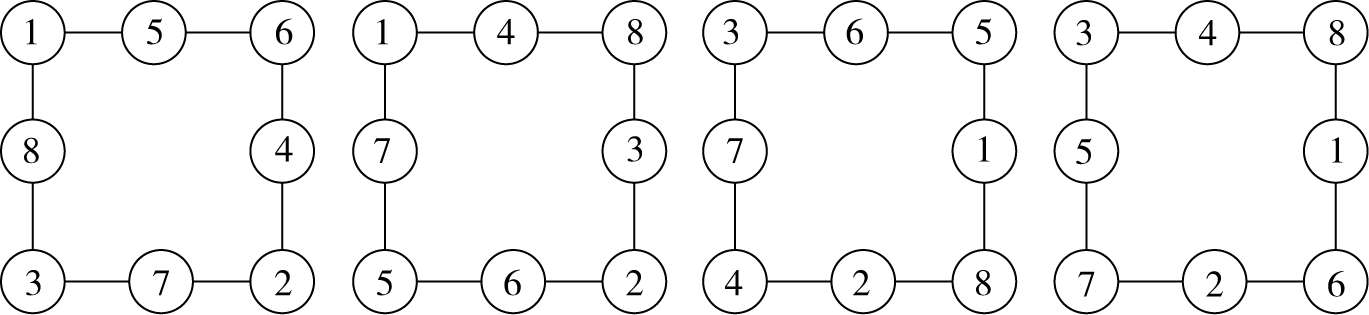
图 81
理一理
以上分拆的是每边和,由在 4 种分拆结果(用在四边上)里“重复出现”,找定四顶点填数。也可由分拆四顶点填数之和来敲定四数。不过要注意的是,分拆结果往往是多样的,当有的结果用来填图遭遇失败,应该及时调换整合。
我们已经学会抓住“关节”来破阵。
当“相等之和”已知,容易抓到“关节”。
当“相等之和”未告知,可以“设码解码”找关节。
有时,如果可能的话,我们也刻意避开“重复”(化纷繁为单纯)去求未知的“相等之和”。如爱因斯坦做过的题里,我们不在错综重叠的 7 个三角形之间纠缠,而只挑选倒置的 3 个三角形“▽”。这 3 个三角形不重复、不遗漏地涉及全部 9个数。于是可以轻而易举地求得每个三角形顶点上的三数和。
相信小朋友们能顺利拿下这个数阵。信心和勇气是积极思维的动力。
1.把 1、2、3、4、5、6 分别填入各○内,使横行三数之和与竖行四数之和都等于11,都等于 12,都等于 13。(图 82)
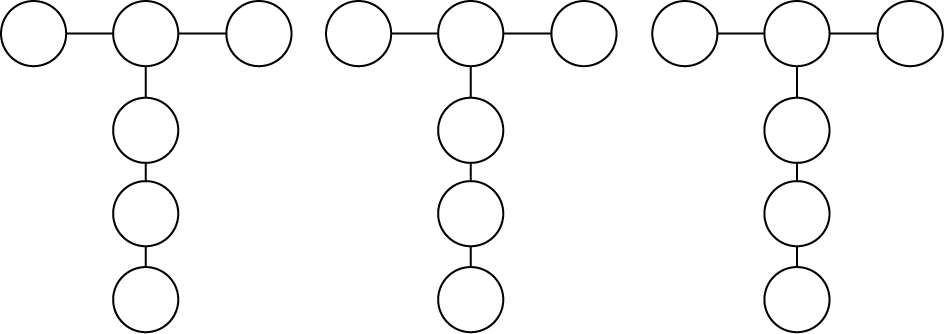
图 82
2.把 1 ~8 八个自然数分别填入各○内,使每个五边形上五数之和都是 21。(图 83)
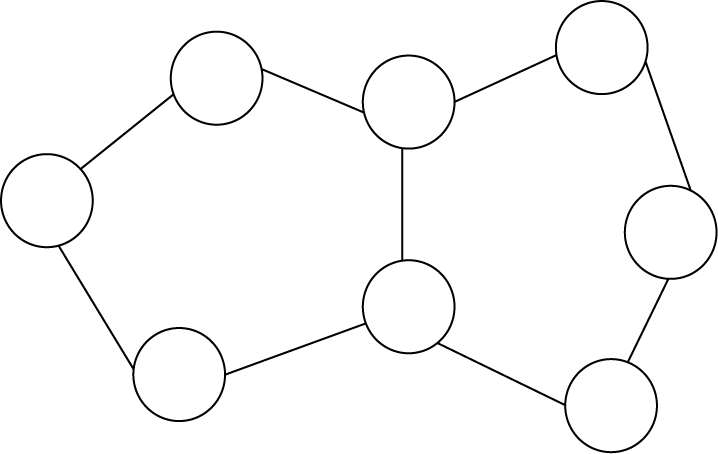
图 83
3.把 1 ~9 九个自然数分别填入各○内,使三角形每边四数之和都相等。(图84)
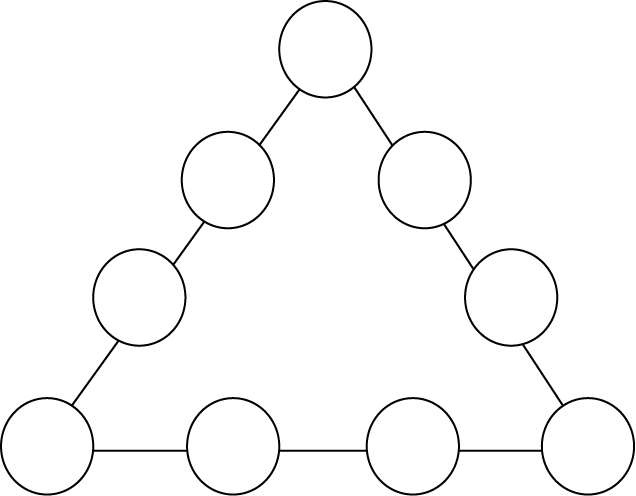
图 84
4.把 7 ~14 八个自然数分别填入各□内,使横行、竖行上的三数之和都相等。(图 85)

图 85
5.只用 2、3、5(可重复使用)填入各内,使每个三角形三个顶点上的三数之和都相等。(图 86)
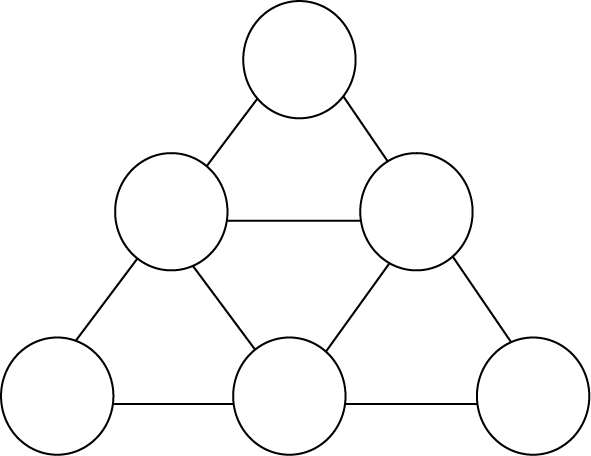
图 86
6.把 2 ~9 八个自然数填入各口内,使横行五数之和与竖行四数之和相等。(图 87)
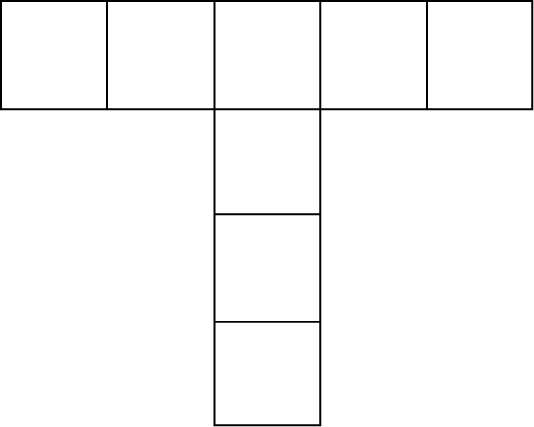
图 87
7.把 2、4、6、8、12、14、16、18 分别填入各□内,使每条横线、竖线、斜线上三数之和都是 30。(图 88)
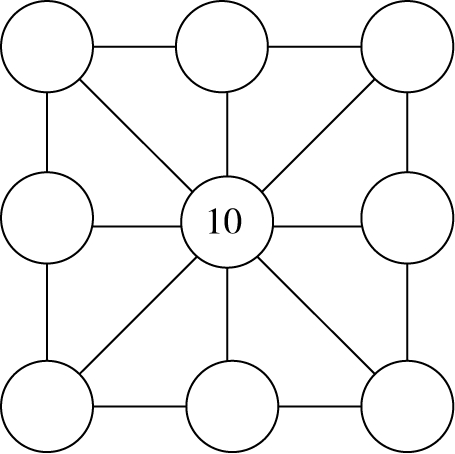
图 88
8.把 1、2、3、4、6 填入各○内,使每条线上三数之和与每个大圆上三数之和都等于 12。(图 89)
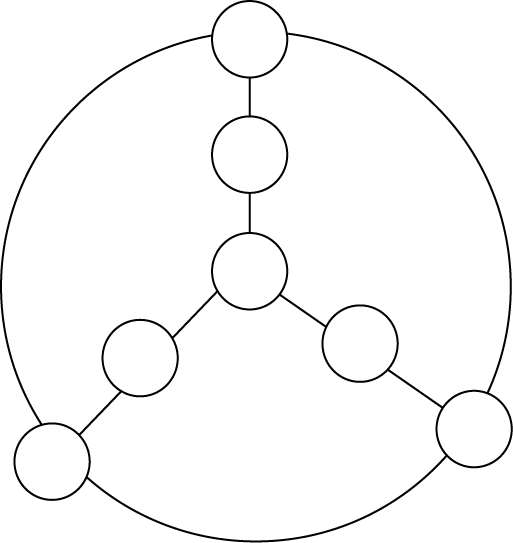
图 89


