




所谓探索分析,指的是对变量进行更为深入的描述性统计分析。它在一般描述性统计的基础上,增加有关数据其他特征的文字与图形描述,显得更加细致与全面,有助于用户思考对数据进行进一步分析的方案。

探索分析的内容一般包括:
(1)检查数据是否有错误,过大或过小的数据均有可能是奇异值、影响点或错误数据。
(2)获得数据分布的特征,很多统计方法都要求数据分布服从正态分布,在探索分析中,一般使用Q-Q图检验。
(3)对数据规律的初步观察,可以获得数据的一些基本规律,如分类变量是否线性相关,这时需要进行方差齐性检验,比较各个分类的方差是否相同,在探索分析中,一般使用Levene检验。
1.研究问题
1847 名广告被调查者年龄资料,数据如图 3-39 所示,试作探索性分析。
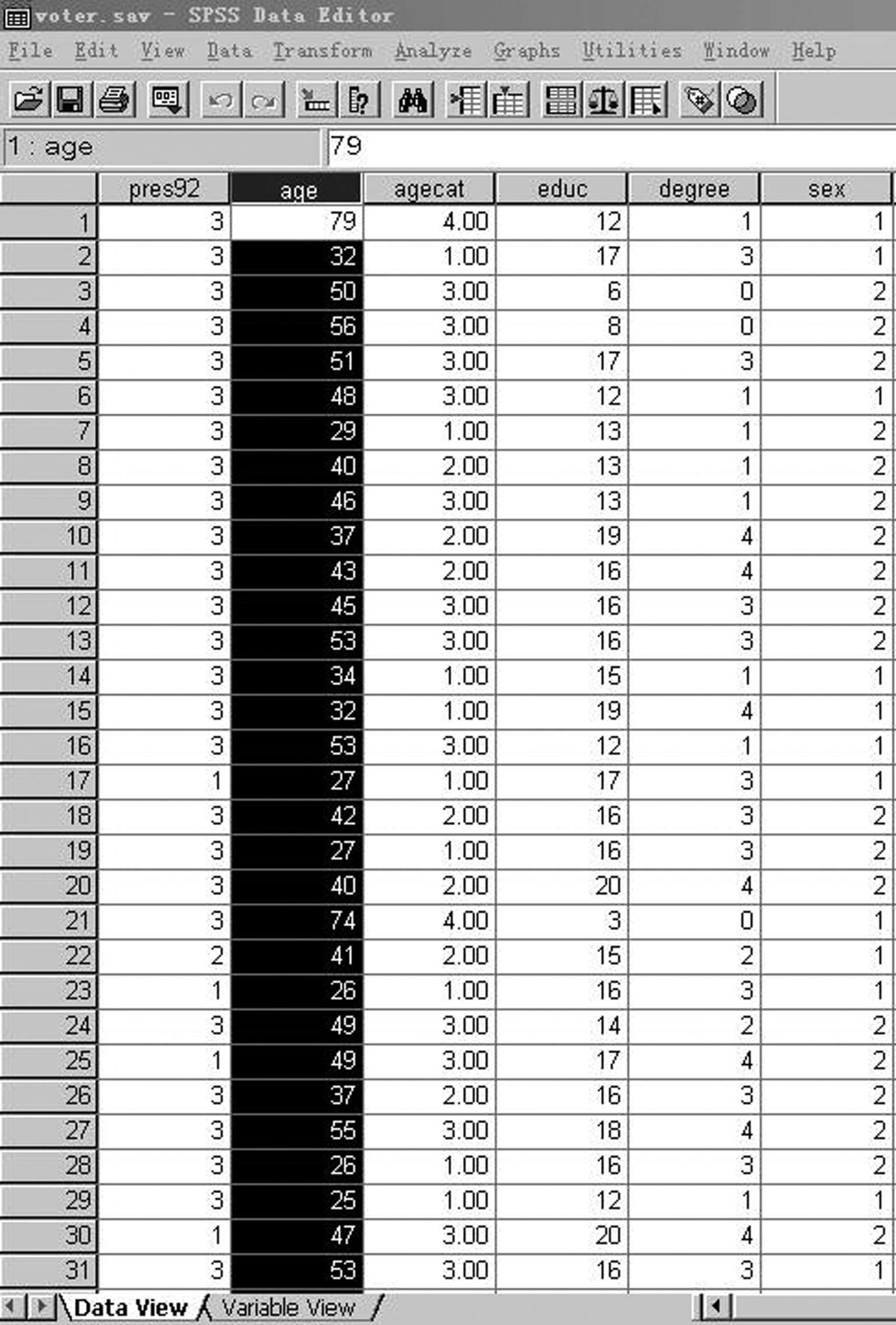
图3-39 被调查者年龄资料
2.实现步骤
(1)单击“Analyze”菜单“Descriptive Statistics”项中的“ Explore”命令,弹出“Explore”对话框,单击
 按键使对话框左侧的变量选择“年龄”作为分析变量,添加到“Dependent List”框中,再选中对话框左侧的“性别”作为分类变量,添加到“Factor List”框中。“Display”框中默认“Both”,表示输出图形和描述统计量,此项可以激活右边的“Statistics”和“Plots”两个按钮。如图 3-40 所示。
按键使对话框左侧的变量选择“年龄”作为分析变量,添加到“Dependent List”框中,再选中对话框左侧的“性别”作为分类变量,添加到“Factor List”框中。“Display”框中默认“Both”,表示输出图形和描述统计量,此项可以激活右边的“Statistics”和“Plots”两个按钮。如图 3-40 所示。
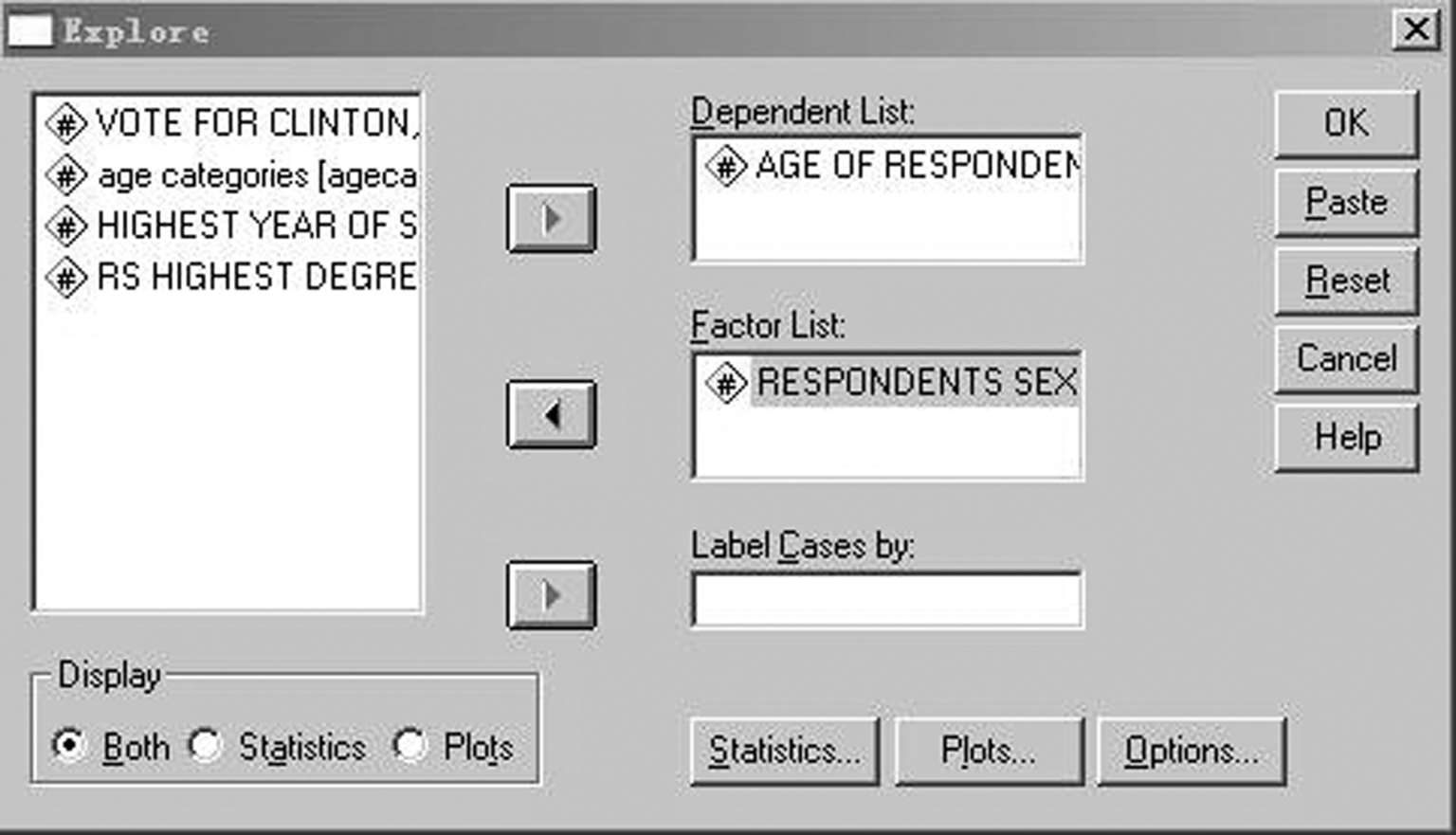
图3-40 “Explore”对话框
(2)单击“Explore”对话框右下方的“ Statistics”按钮,出现“Explore:Statistics”对话框,如图 3-41 所示,全部选中框里项目,“Descriptive”表示输出平均数、中位数、众数、5%修正均数、标准误差、方差、标准差、最小值、最大值、全距、四分位全距、峰度系数、峰度系数的标准误差、偏度系数、偏度系数的标准误差。置信度系统默认为 95%;“M-estimators”表示作中心趋势的粗略最大似然确定,输出 4 个不同权重的最大似然确定数,当数据分布均匀,并且两尾巴较长,或当数据中存在极端数值时,“M-estimators”可以提供比较合理的估计;“Outliers”表示输出 5 个最大值和 5 个最小值;“Percentiles”表示输出第 5%、10%、25%、50%、75%、90%、95%百分位数。单击“Continue”按钮返回“Explore”对话框。
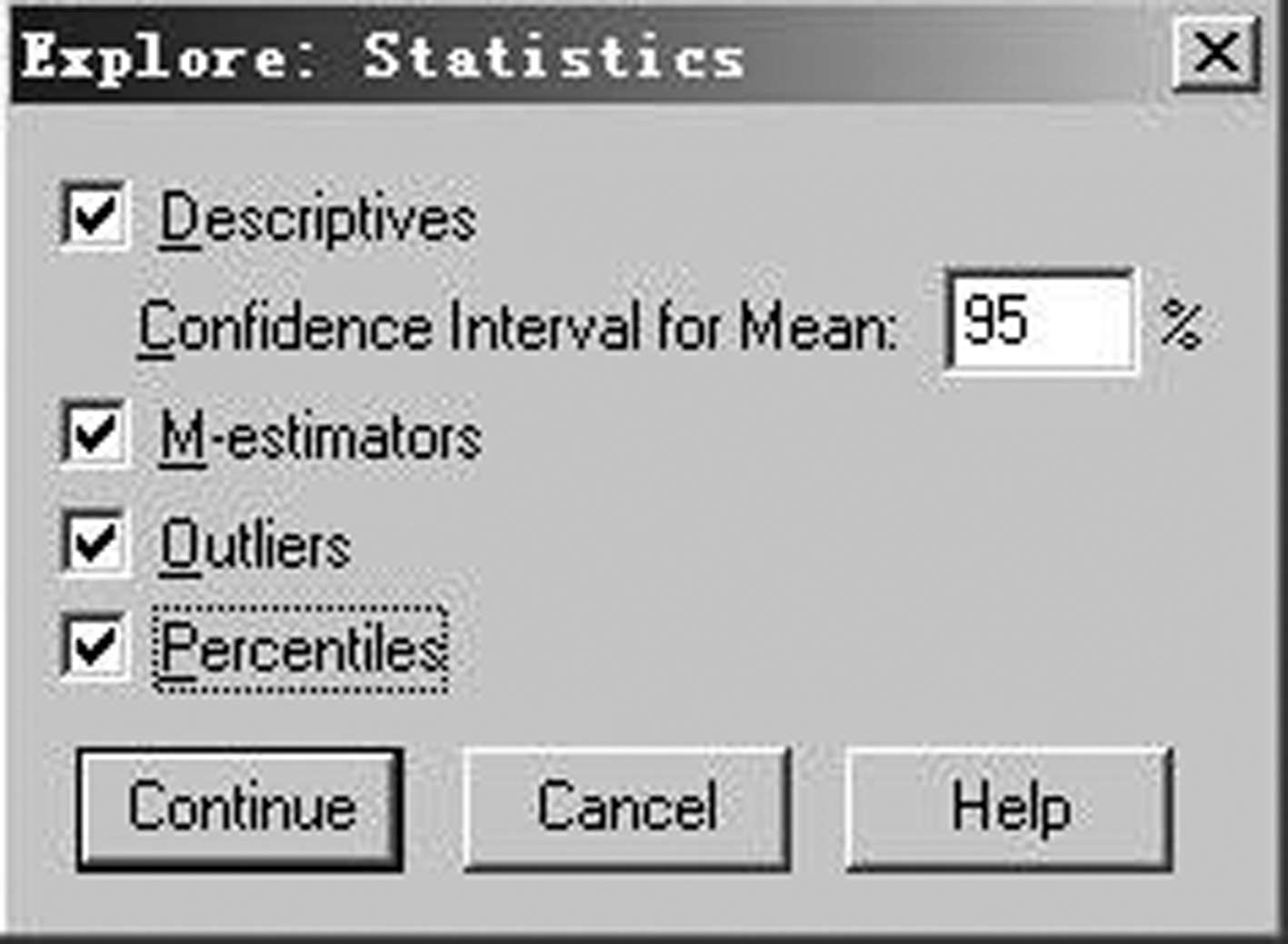
图3-41 “Explore:Statistics”对话框
(3)单击“Explore”对话框右下方的“Plots”按钮,出现“Explore:Plots”对话框,如图 3-42 所示,系统默认“Boxplots”框中的“Factor levels together”和“Descriptive”框中的“Stem-and-leaf”。“Factor levels together”表示要求按照分类进行箱图绘制;“Stem-and-leaf”表示作茎叶情形描述。选中“Normality plots with tests”表示输出显示正态分布的图形,同时输出Kolmogorov-Smirnov统计量中的Lilifors显著性水平。选中“ Spread vs.Level with Levene Test”框中的“ Power estimation”,表示对每一组数据产生一个中位数范围的自然对数与四分位范围的自然对数的散点图。单击“Continue”按钮返回“Explore”对话框。
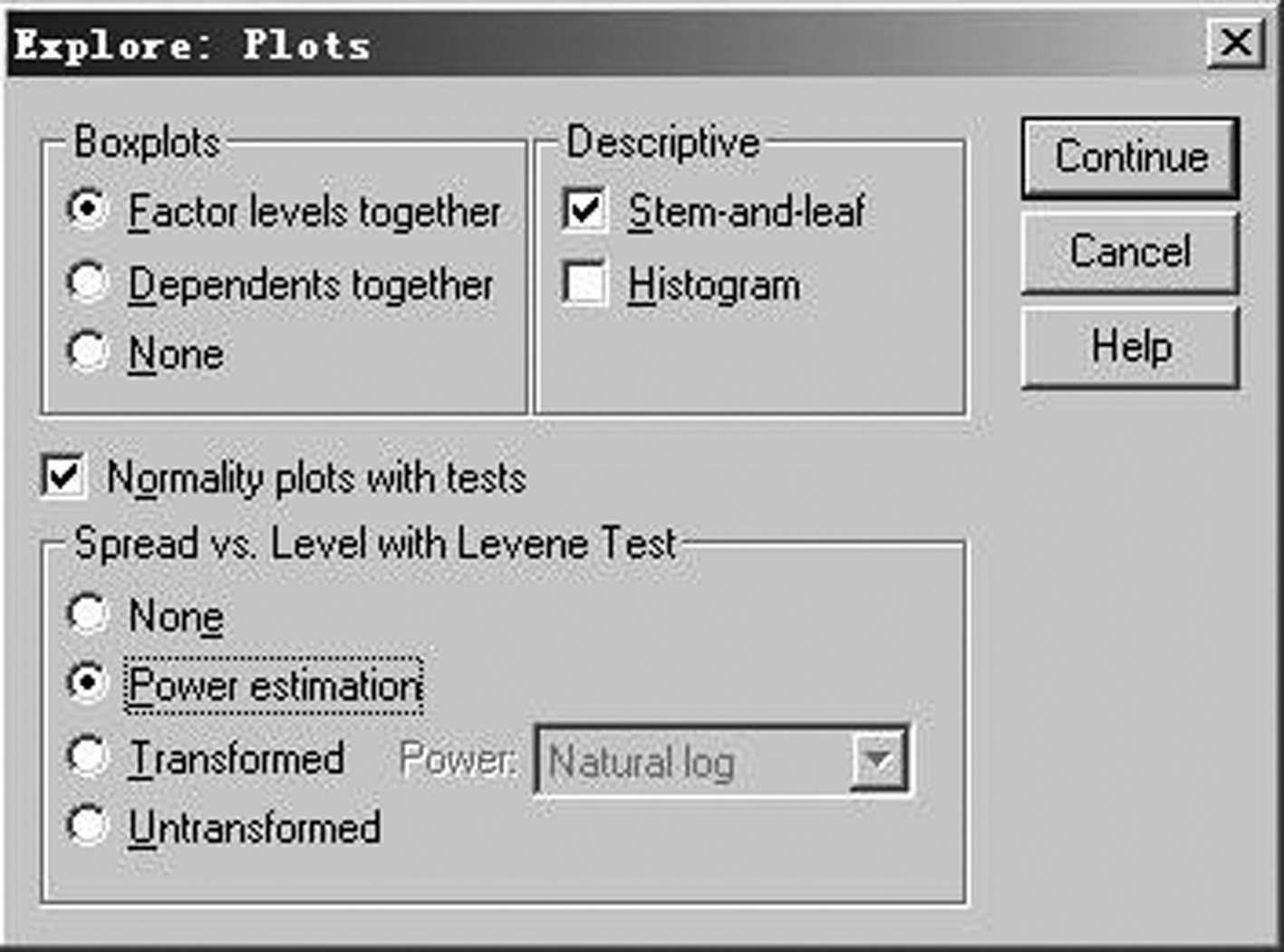
图3-42 “Explore:Plots”对话框
(4)单击“Explore”对话框右下方的“Options”按钮,出现“Explore:Options”对话框,如图 3-43 所示,系统默认“Missing Values”框中的“Exclude cases listwise”,表示去除所有含缺失值的个案后再进行分析。单击“ Continue”按钮返回“ Explore”对话框。
图3-42 “Explore:Options”对话框
3.结果和讨论
在结果输出窗口中可以看到如下统计数据。
(1)首先输出如图 3-43 的个案(样本)观察量总计表,从中我们可以看到,男性个案 804,女性个案 1043,共 1847,无缺失值。

图3-43 观察量总计表
(2)然后输出图 3-44,该图表示被调查者年龄的分类描述统计结果。表上半部分是男性年龄的统计,其中包括平均数为 47.68,平均数的 95%置信区间为46.60—48.75,中位数为 46.00,5%修正平均数为 47.15,标准误差为 0.547,方差为 240.822,标准差为 15.518,最小值为 22,最大值为 89,全距为 67,四分位全距为24,偏度系数为 0.467,偏度系数标准误差为 0.086,峰度系数为-0.549,峰度系数标准误差为 0.172。下半部分是女性年龄的统计信息。
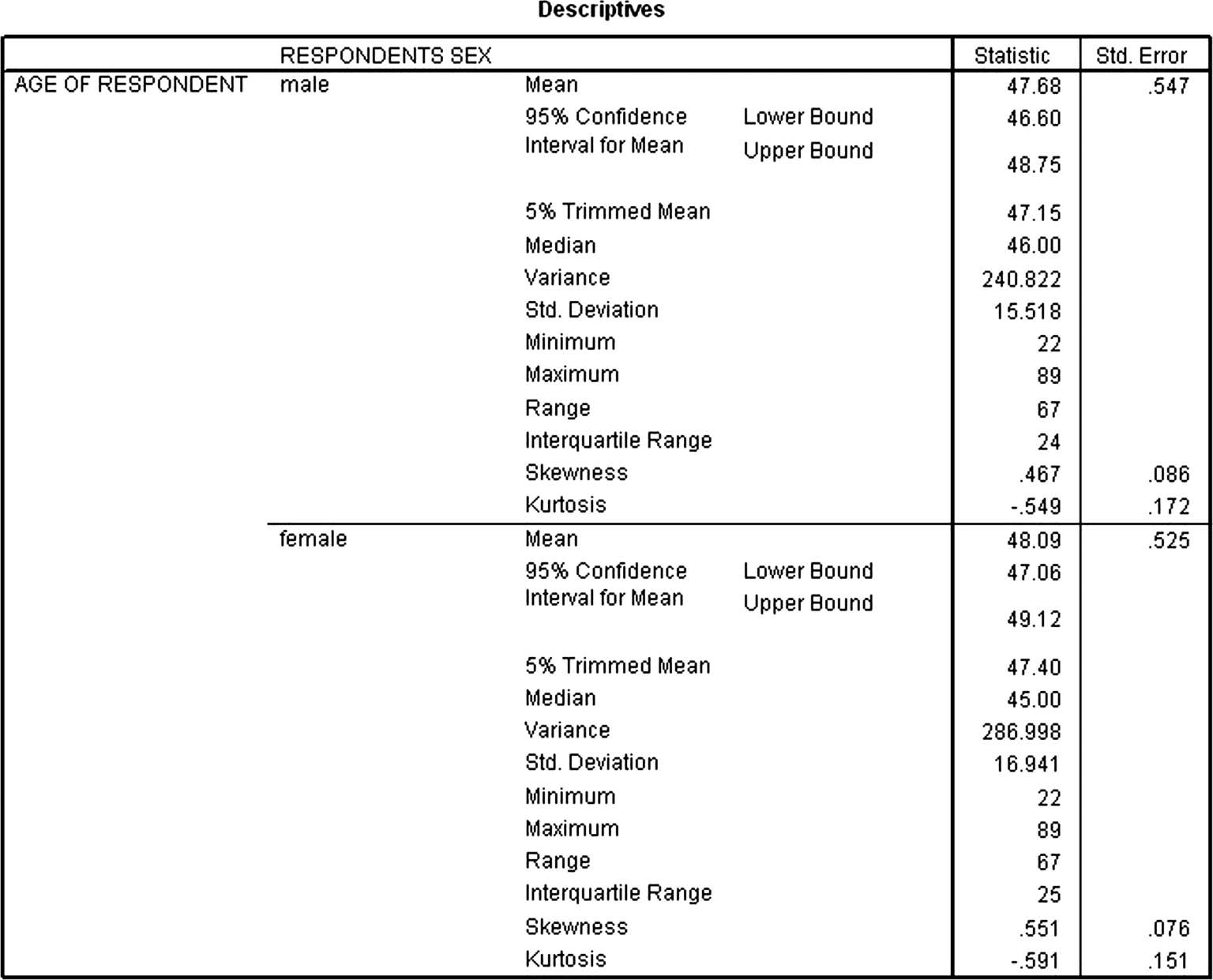
图3-44 被调查者年龄的分类描述统计结果
(3)接着输出如图 3-45 所示的四个不同权重下作中心趋势的粗略最大似然确定数,图下的a、b、c、d表示四种加权常数。对于伴有长拖尾的对称分布数据或带有个别极端数值的数据,用粗略最大似然确定数替代平均数或中位数,结果更准确。图 3-45 估计量结果与图 3-44 平均值相比较,发现平均值要比M估计值大(男性= 47.68,女性= 48.09 ),这是因为数据呈现正偏态分布,平均值就受到较大值的影响。值得注意的是,在对数据进行正态分布的检验时,几乎都有理由认定数据拒绝正态分布假设,但如果数据个案足够多,样本量足够大,进行统计计算时就不必强求观测量一定要服从正态分布,只要数据接近正态分布就行了。


图3-45 四个不同权重下作中心趋势的粗略最大似然确定数
(4)再输出百分位数,也是分类后的百分位数。如图 3-46 所示。

图3-46 百分位数
(5)分别输出两类中最大的 5 个数和最小的 5 个数,并且包括这些值对应的个案编码,如图 3-47 所示。
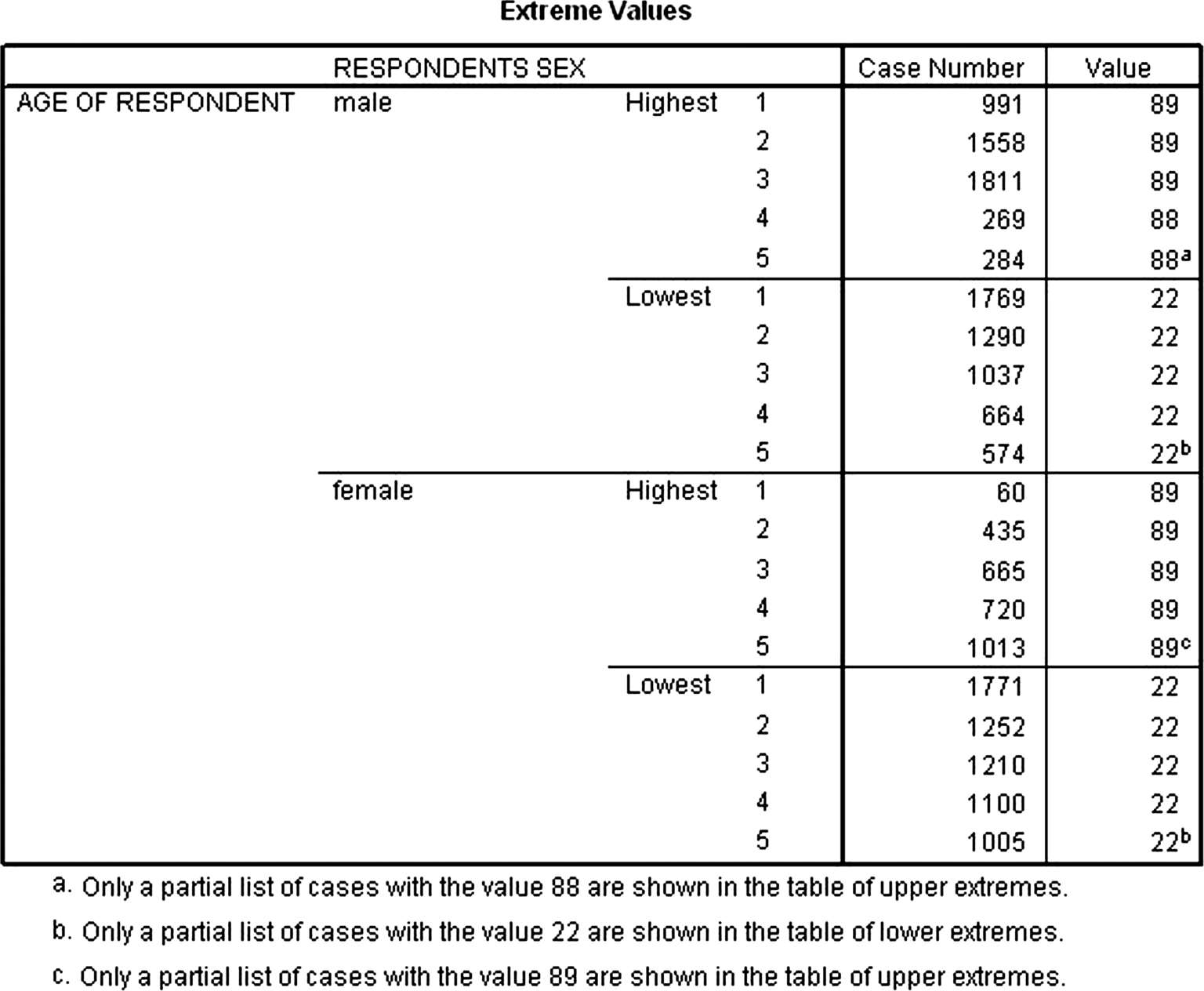
图3-47 两类中最大的 5 个数和最小的 5 个数
(6)输出正态分布和方差齐性检验结果。图 3-48 我们可以看出,男性和女性数据均符合正态分布。图 3-48 中,各个列的输出结果分别是取值标准、Levene统计量、自由度 1、自由度 2 和显著性水平。其中取值标准有:平均值、中位数、中位数和调整后的自由度、调整后的平均值 4 个。从 4 个指标得到的显著性水平看,都大于 0.05,因此可以确定接受方差相等的零假设。

图3-48 正态分布检验结果
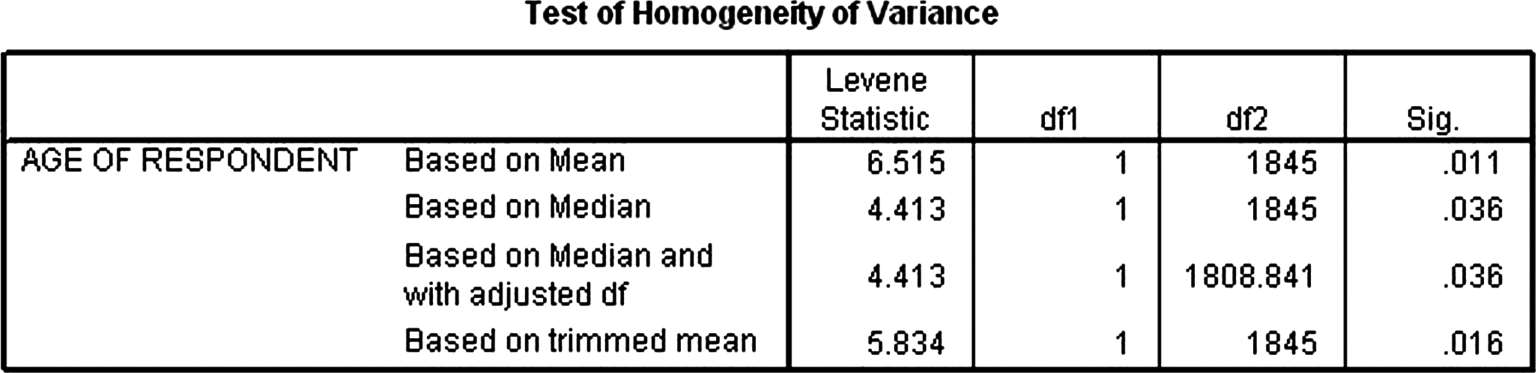
图3-49 方差齐性检验结果
(7)系统还进行数据的茎叶情形描述。茎叶自左向右可以分为三大部分:频数(Frequency)、茎(Stem)、叶(Leaf)。茎表示数值的整数部分,叶表示数值的小数部分。每行的茎和每个叶组成的数字相加再乘以茎宽(Stem Width),即茎叶所表示的是实际数值的近似值。图 3-50 是男性年龄的茎叶图,该图最后一行表示每个叶表示3 个个案。以第一行数据为例,频数为31,茎为2,叶为0.2233334444,茎宽为 10,按照观测量的近似值= (茎+叶)×茎宽的公式,第一个观测量的值为(2+ 0.2)× 10 = 22,依次类推,这一行 10 个年龄变量的值大约为:22、22、23、23、23、23、24、24、24、24。图 3-51 是女性年龄的茎叶图,分析同上。

图3-50 男性年龄茎叶图

图3-51 女性年龄茎叶图
(8)系统输出箱图,如图 3-52 所示。图中方箱为箱图主体,上中下 3 条线分别表示变量值的第 75、50、25 百分位数,因此变量的 50%观察值落在这一区域中。方箱中的中心粗线为中位数,箱图中的触须线是中间的纵向直线,上端截至线为变量的最大值,先端截至线为变量的最小值。如果存在奇异值,箱图中会用“0”标记,存在极值,则会用“*”标记。
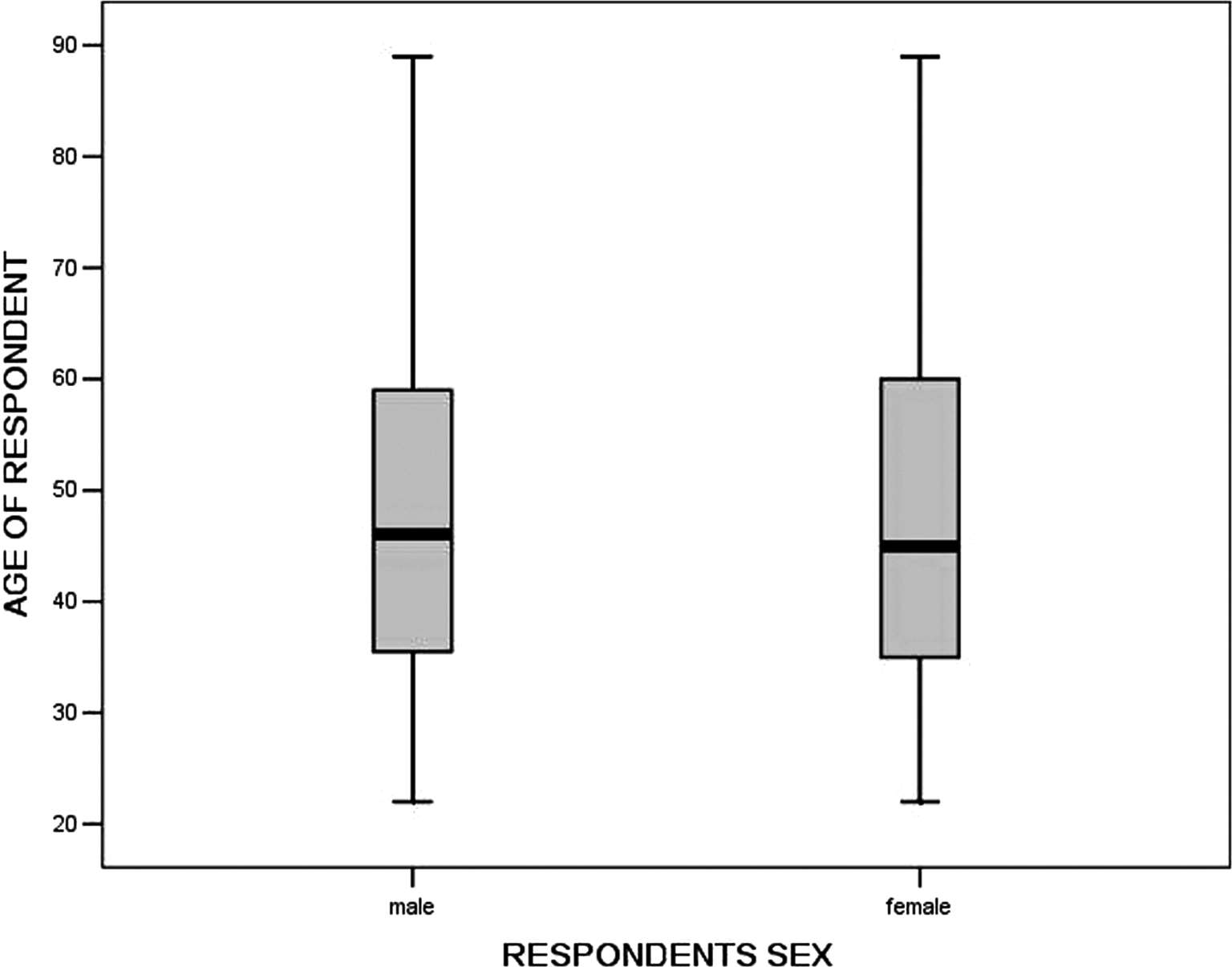
图3-52 箱图
(9)输出Spread vs.Level with Levene Test图,如图 3-53 所示。该图用来检验数据的方差奇性,图中的Slope为回归斜率,Power for transformation为进行数据幂转换的幂值,即为使两个方差相同,对数据进行幂转换的幂值。它们之间的关系为幂值= 1-回归斜率。
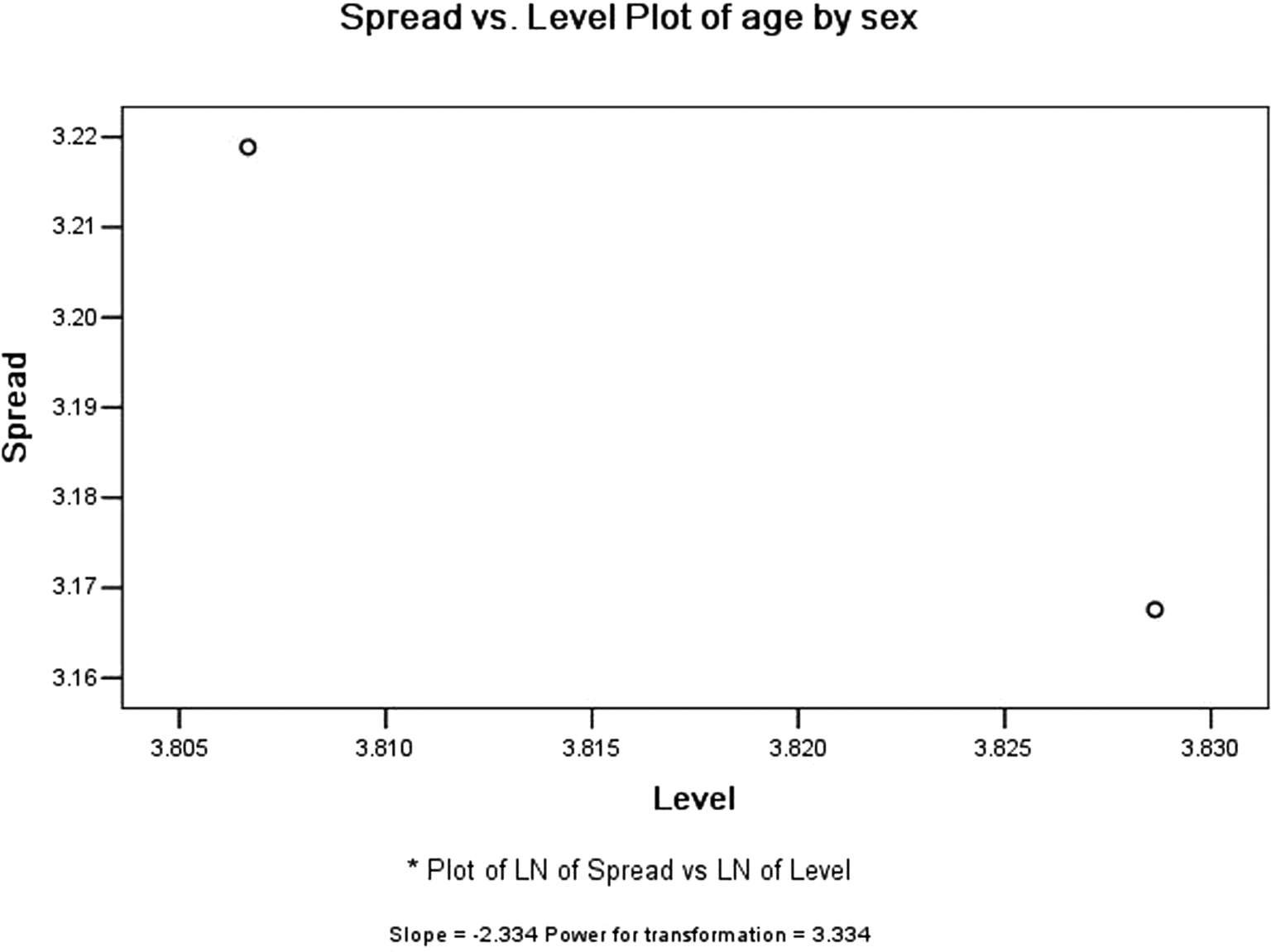
图3-53 检验方差奇性图
(10)输出年龄正态概率Q-Q图,如图 3-54、3-55 所示。图中斜实线为正态分布的标准线,散点图实际数据取值,散点图组成的曲线越接近斜实线,表明数据分布越接近正态分布。从图中可以看出,大部分点都接近图中斜实线,可认为男性、女性年龄分布均接近正态分布。
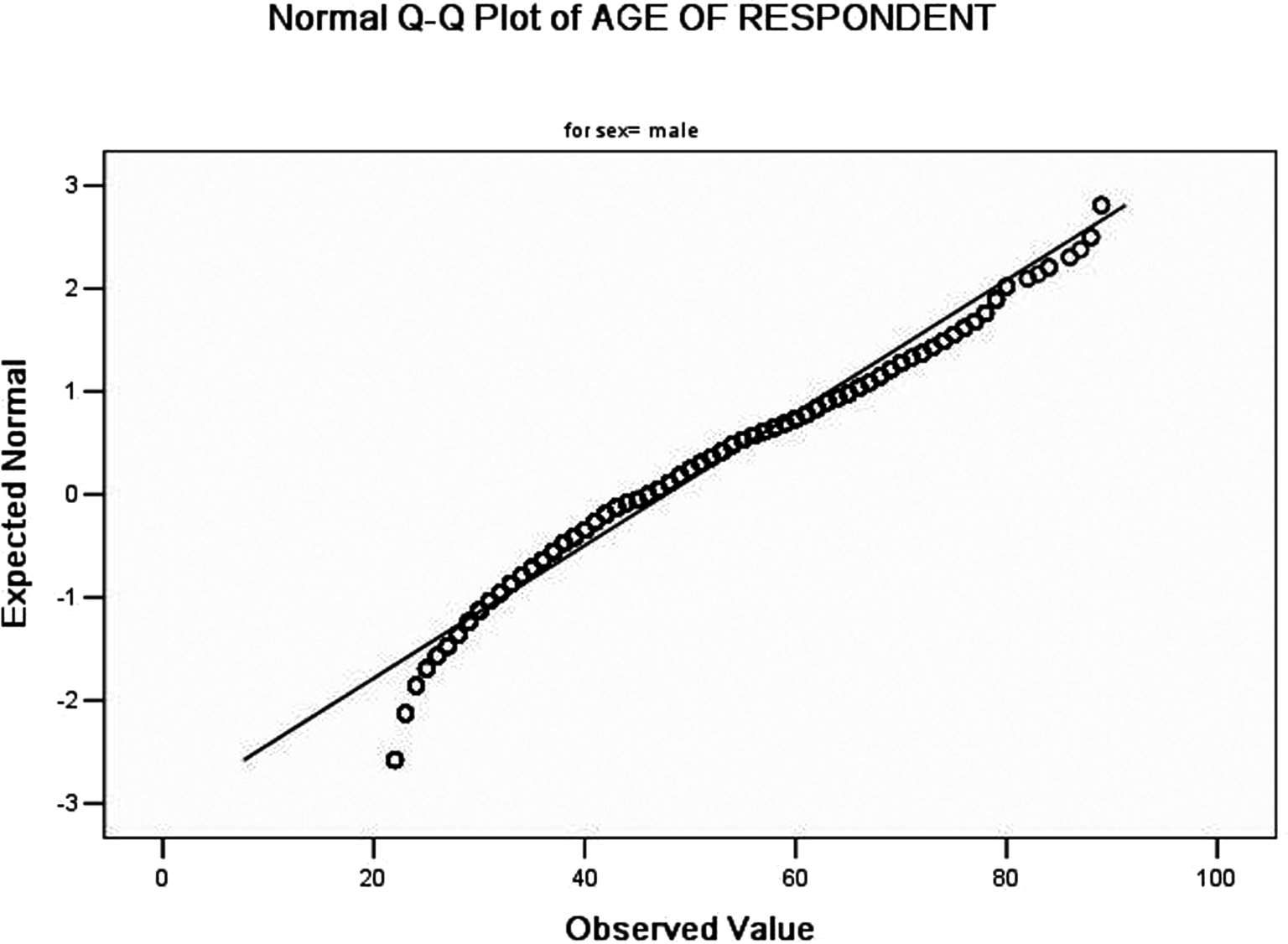
图3-54 男性年龄正态Q-Q图
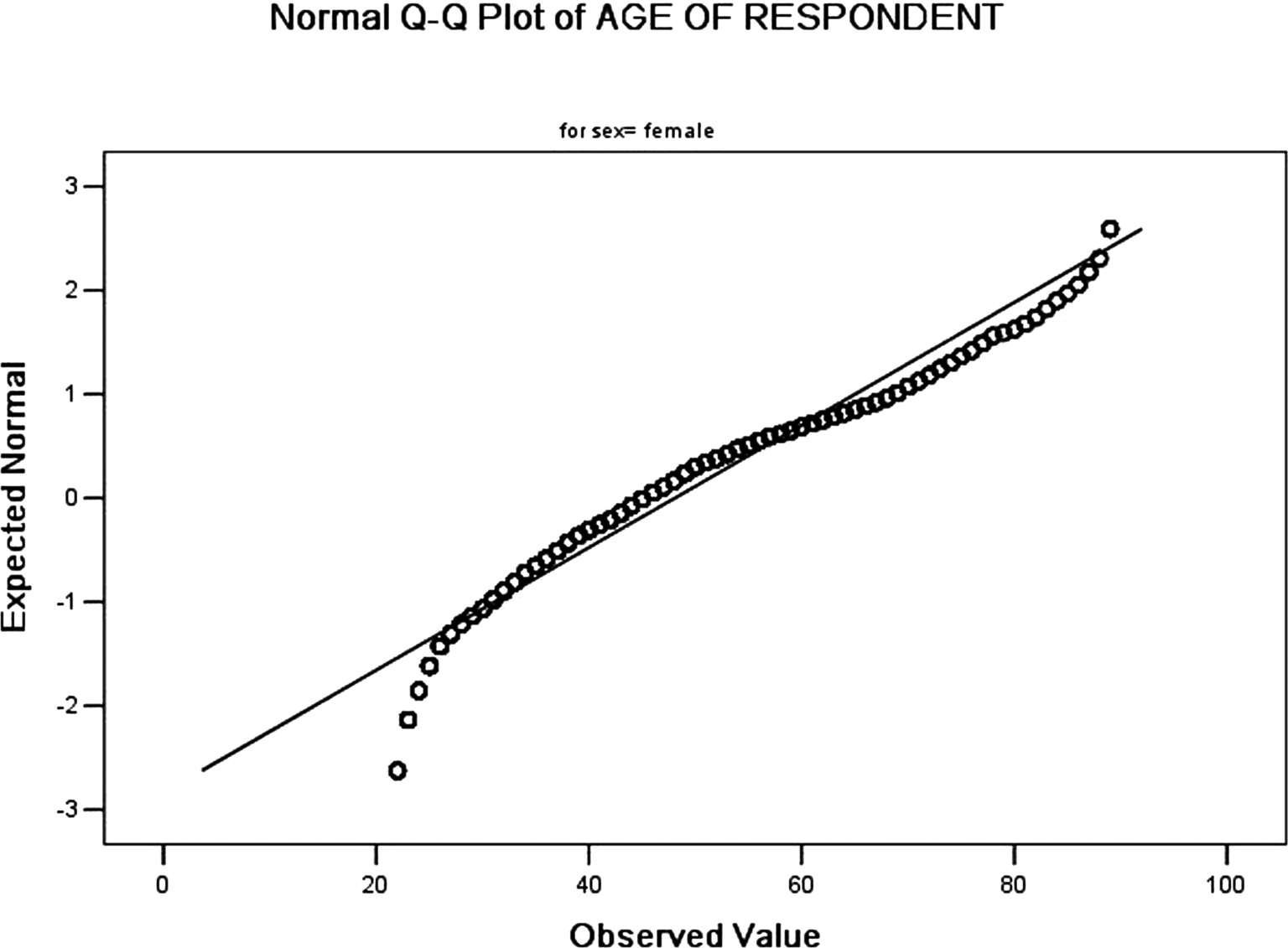
图3-55 女性年龄正态Q-Q图
(11)输出离散正态概率Q-Q图,如图 3-56、3-57 所示。图中横坐标是年龄,纵坐标是和正态分布的偏离。从两个图我们可以看出,这些点近似随机落在中间横线周围,少数几个点偏离横线,我们可以认为,男性、女性年龄的分布不能拒绝正态分布。
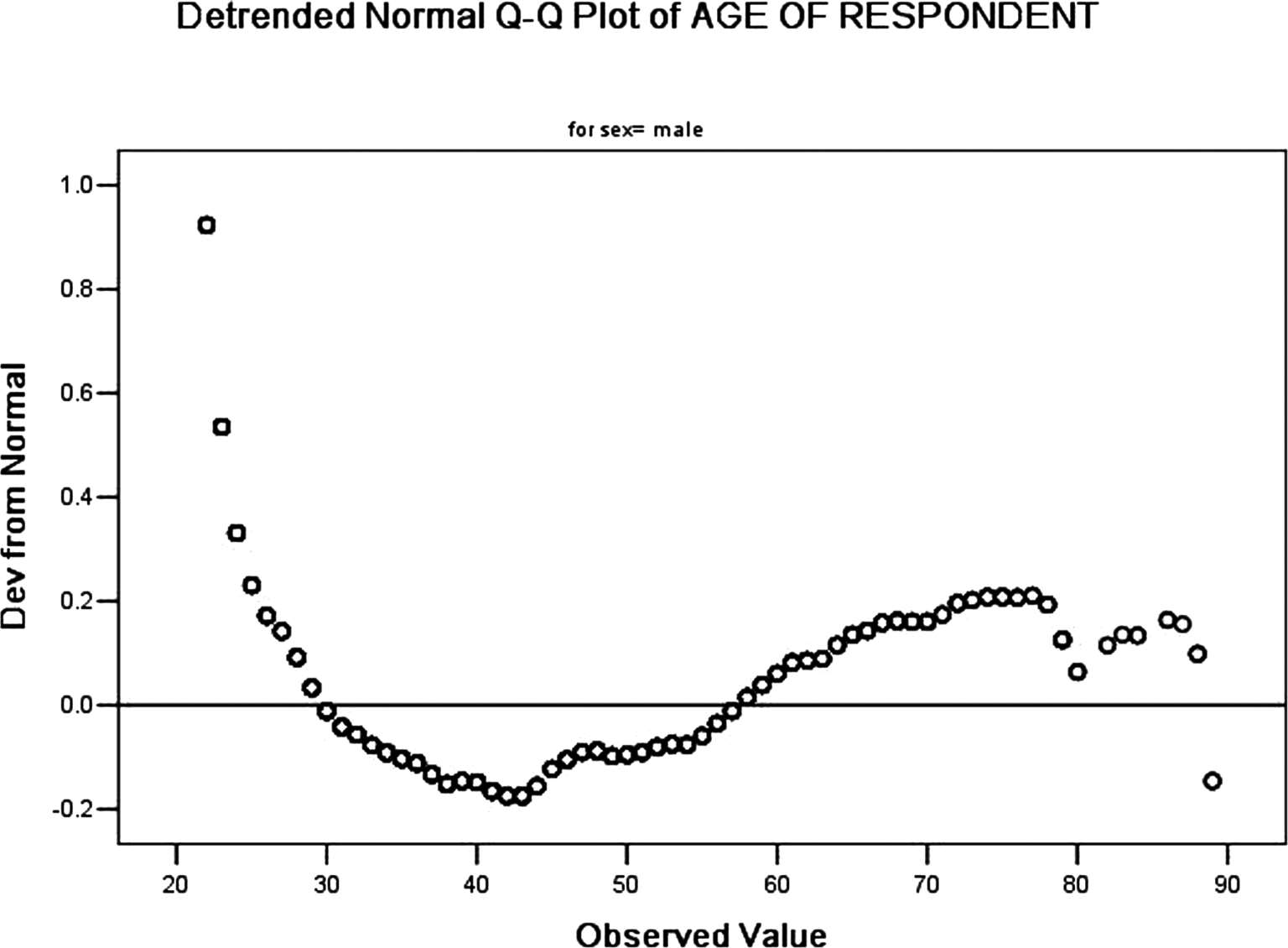
图3-56 男性年龄离散Q-Q图
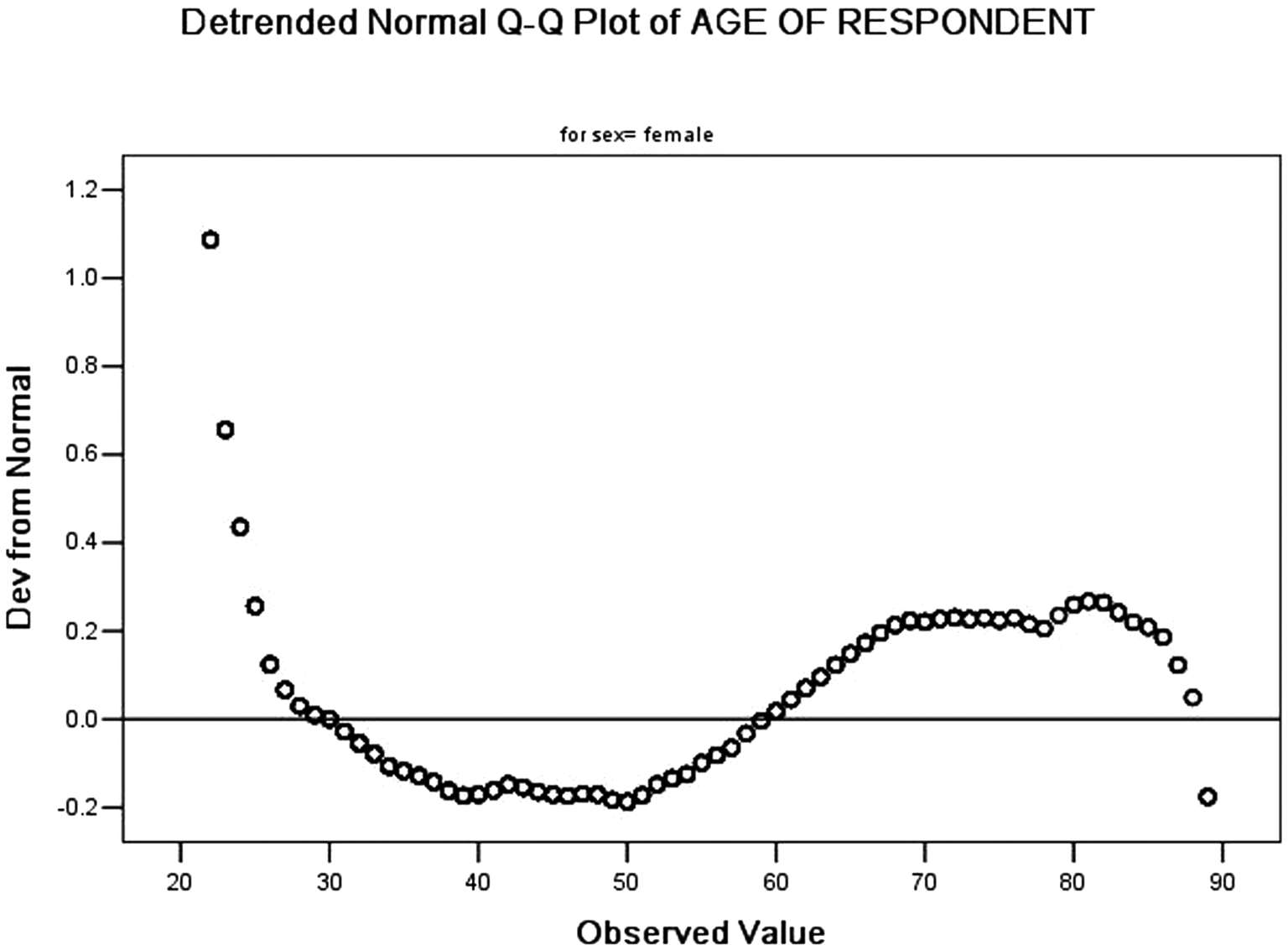
图3-57 女性年龄离散Q-Q图