




“人不能两次踏进同一条河流”是古希腊哲学家赫拉克利特(约前540—约前480与前470之间)说的。他创立了一种“变”的哲学,其中充满了辩证法思想,对后来辩证法的发展产生了重大影响。赫拉克利特用非常简洁的语言概括了他关于运动变化的思想:“一切皆流,无物常驻。”在他看来,宇宙万物没有什么是绝对静止和不变化的,一切都在运动和变化。在他的思想中,运动是绝对的,静止是相对的。然而更进一步,赫拉克利特所描述的“动”其实含有很强的不确定性。按照随机过程的理论,一个连续时间随机过程中出现两条完全相同路径的可能性为0!
人生中有太多的不确定性,随之而来的是惊喜、期盼、失望、不甘、无奈等情绪,这表明了这些不确定性似乎和精确的数学格格不入,但我们仍然可以用数学中的一个重要分支——随机过程,来解释生活中的不确定性。俗话说“谋事在人,成事在天”,表明了人的主观努力也会受到不确定的环境的影响。
随机过程是一门深奥的数学理论,一般是数学系高年级本科生和研究生的专业课,其先修课程一般包括概率论、数理统计等,研究前沿方兴未艾。
随机过程研究一族随机变量,如果这些随机变量的指标是时间,那么简单地说,这样的随机过程是一个以时间为标志的不确定过程。在这个过程中,站在现在这个时间点上看,过去已经是已知的、确定的,而将来的任何时刻都是一个随机变量。如果这个过程的发展遵循一定的规律,我们可能可以摸索出未来的随机变量的分布。也就是说,虽然不知道未来会发生什么事,但有可能知道未来发生某些事的概率。例如,我们用几何布朗运动来刻画风险资产价值 S t 的运行轨迹,简化该过程,则 S t 满足随机微分方程
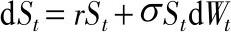

骰子
这里, W t 是维纳过程,或者叫布朗运动; r 和 σ 分别表示 S t 的数学期望回报率和波动率。虽然 S t 对未来的时间 t 是随机的,但这两个参数决定了风险资产未来的数学期望值和随机波动的大小。
人生如果要用一个模型来刻画,随机过程自有其妙处。如果说我们的人生由一只看不见的命运之手牵引,我们也可以像刻画风险资产价值的运行轨迹那样用随机过程来描述这只手。这个过程有几个特点是肯定的:
● 关于时间是连续的、不可逆的;
● 有时间上限,当然这个时间上限也是随机变量;
● 这个过程包括随机跳跃的过程,跳跃的过程可以是内在的,也可以是外生的;
● 人们的出身决定了这个过程的初始状态;
● 这个过程受外在因素,如大环境的影响很大;
● 每个人的过程都有独特之处,但与周围人的过程有很大的相关性,且互相影响;
● 对这个过程,人们自己能做的事就是调整过程的参数,并在一定的时机选择跳入不同的子过程。
于是,我们可以解释、推演下面几件事。
● 所谓的命运不是决定性的,它控制了大方向,这包括我们出生的年代、生活的大环境等,但我们仍然有希望在一定程度上,通过自己的努力大大增加达到目标的可能性。
● 调整参数不能改变未来的随机性,但可以使未来的某些事件发生的可能性增大,或者说,在已有信息的基础上,可以通过调整参数,使未来的数学期望更接近当事人的希望。但不要以为你努力了就一定能达到目的。所以,取得成功,应心生感激;不幸失败,当坦然接受。
● 人生很多时候会面临很多选择,这使得后来的进程转入不同的子过程。在这些不同的子过程中,发生各种随机事件的概率是不一样的。有时,随机的外生因素也会使人生轨迹发生改变,导致进入一个与之前不同的子过程。由于面临选择时,你并不能确定未来的随机事件,所以犹豫徘徊不能帮你,事后后悔更是没有意义,应当在分析可能性后,当断则断。
● 按随机过程的理论,过去的信息越多,未来的确定性就越大。对待不确定性这种风险,人们一般有两种态度,有人厌恶风险,有人喜欢冒险。但对于人生,人们倾向于喜欢不确定性,实际上是希望好的随机事件发生。例如,孩提时期,未来的不确定性很大,人们寄予各种各样的祝福;而到了老年,大都尘埃落定,可变性就很小了,不过大器晚成的例子也是有的。
● 大多数人都有攀比心态,其实这没有太大的意义,很多时候只会徒增烦恼,每个人经历的过程不一样,有时小概率事件也会发生,不服气也无益。
● 由于人生的不可逆性,过去发生的事确定了你曾经的轨迹,并会影响你的未来,但这种影响不是决定性的。当你已经站在一个时间点上,在此之前的所有可能性中,只有一种发生了,并得到证实,由于排他性,其他可能性在这个时间点上都没有发生,甚至有时就永远成为不可能事件了。不管这是不是你所希望的,你都只能接受,这时怨天尤人、蹉跎叹息都没有用,积极的态度是站在这个时间点上分析发生的事情和它对未来的影响,未来有各种各样的可能性,你仍然可以继续调整参数。
大环境也是一个随机过程,所有人调整参数的结果共同决定了未来的可能性。于是我们得出结论:大家努力调整参数,不仅要努力调整自己的参数,也要帮助调整别人的参数,还要合力作为,调整好大环境的参数。
随机过程中还有一个重要的概念:鞅。尽管鞅的数学定义比较难懂,但用通俗的语言来讲,它是指一类随机过程,这类随机过程未来的数学期望和初始状态是一样的。以此来看,人生可不是鞅。