2.1.4　正弦波抽取算子

对于遍历性过程，从“集平均”和从“时间平均”的研究是等价的。对于其他类型的信号，从“集平均”的研究和从“时间平均”的研究是不同的。后者是非平稳过程的另一个研究视角。在这里将随机过程看成时变随机变量。其概率密度函数是时变的，所以研究其分时概率框架。具体来讲，就是从分数概率分布函数的定义出发，研究这类信号的性质。其主要优点是可以通过单观测样本估计信号的统计量，适用于实际应用中的某些特殊的不能够重复观测或者观测数据所需要的成本较高的场景。

正弦波提取算子 ^[111] 与傅里叶级数的定义相似，基于此可定义分时概率框架中的概率分布、概率密度和期望算子，因此在循环平稳信号处理中发挥了至关重要的作用，具体表示如下

（2.47）

该算子的物理含义为提取信号 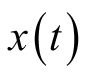中的正弦波分量 及其强度。当信号 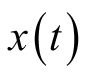是周期信号时，上述定义中的系数就是傅里叶级数的系数。

在后续应用中，有时候我们只关注正弦波分量的强度。因此，将等式（2.47）中的系数部分定义为另一个算子，即

（2.48）

其具体应用见第4章和第5章。

示性函数 是定义分时概率框架中概率分布函数的另一个重要函数，具体定义为

（2.49）

相应地，通过示性函数的 阶乘积定义关于信号 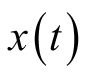的函数为

（2.50）

其中向量 和时延参数向量 。当信号 为复信号时，对应的由示性函数定义的函数为

（2.51）

其中 和 分别表示 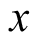的实部和虚部。“分时”的名称由此函数而来，以一维示性函数为例， 将时间轴分为两部分，同理 将 维空间也分为两部分。根据此函数和正弦波分量提取算子，分时概率框架中的概率分布函数定义如下。

定义3 分时概率框架中循环平稳信号 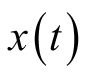的“概率”分布函数为

（2.52）

在此基础上可发展“概率”框架中的“概率”密度、分布和各阶统计量等函数。 rkLdx8Mjoqq5MjPeMJ2pLEwDPb4u7gqcLhRmlC+pnX9mTHbd8WJaeO4usxbIKq4A