




随机过程是刻画信号随时间变化的另一种函数,不同于确定性信号在每个时刻的情况是确定的,随机信号在每个时刻的变化情况不确定但是服从一定的规律。因此,随机过程是二维的信号,记作
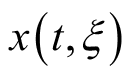 ,其中
,其中
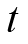 表示信号随时间的变化,
表示信号随时间的变化,
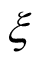 表示信号在每个时刻的不确定性。当
表示信号在每个时刻的不确定性。当
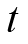 固定时,
固定时,
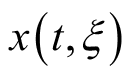 成为一个随机变量,其取值来自一个样本点集合。因此,也称
成为一个随机变量,其取值来自一个样本点集合。因此,也称
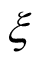 为集合维度。当
为集合维度。当
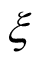 固定时,
固定时,
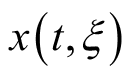 成为一个样本,是一个随时间变化的确定性函数。因此,也称
成为一个样本,是一个随时间变化的确定性函数。因此,也称
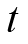 为时间维度。
为时间维度。
在随机过程的分析过程中,往往是通过固定一个或多个时刻,从统计的角度考察随机过程的特性。在这些过程中,涉及的数学期望运算都是集合上的平均。例如,通过固定一个时刻,可以考察随机过程的一阶统计量随时间的变化规律;通过固定两个时刻,得到两个随机变量,由这两个随机变量的特性可以刻画随机过程的二阶统计特性。所以,在不引起歧义的前提下,随机过程简记为
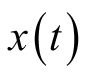 。当然,也可以通过固定
。当然,也可以通过固定
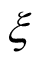 来考察随机信号的特征,这个时候往往涉及随机过程的遍历性,计算的是样本关于时间的平均。接下来会介绍随机过程关于时间平均和集合平均的异同。
来考察随机信号的特征,这个时候往往涉及随机过程的遍历性,计算的是样本关于时间的平均。接下来会介绍随机过程关于时间平均和集合平均的异同。
由随机过程的概念可知,随机过程
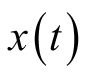 在每个固定时刻都是一个随机变量。因此,可以通过固定每个时刻求取随机变量的一阶数字特征来考察随机过程的一阶特征随时间的变化情况。随机过程的数学期望表示为
在每个固定时刻都是一个随机变量。因此,可以通过固定每个时刻求取随机变量的一阶数字特征来考察随机过程的一阶特征随时间的变化情况。随机过程的数学期望表示为
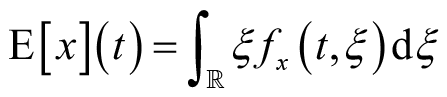 (2.12)
(2.12)
E[·]是数学期望算子,
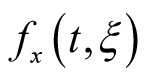 表示随机过程
表示随机过程
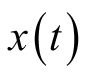 在
在
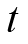 时刻的概率密度函数。
时刻的概率密度函数。
对于一个随机过程
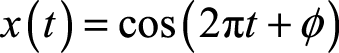 ,其中
,其中
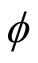 是
是
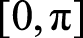 上的均匀分布。当固定任何一个时刻
上的均匀分布。当固定任何一个时刻
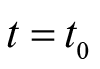 时,有
时,有
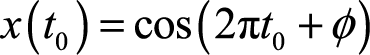 。此时,我们只能获得该随机信号在
。此时,我们只能获得该随机信号在
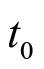 时刻的统计规律,而不知其具体的取值。此信号的数学期望为
时刻的统计规律,而不知其具体的取值。此信号的数学期望为
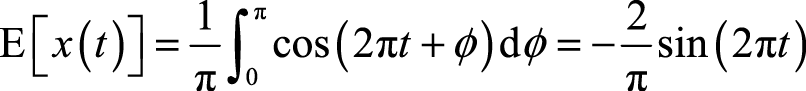 (2.13)
(2.13)
正如定义中所指明的,这里的求平均运算是从集合维度进行的,所以随机过程的数学期望是时间的函数。若随机变量
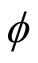 是
是
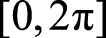 上的均匀分布,则信号
上的均匀分布,则信号
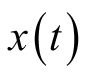 的数学期望为
的数学期望为
 (2.14)
(2.14)
对比等式(2.13)和等式(2.14)可知,随机过程的数学期望的值可以是随时间变换的函数或者常数。根据一阶统计量是否随时间变化,可以将随机信号分为一阶平稳随机过程和一阶非平稳随机过程。这里“平稳”的含义是指信号的一阶统计特性不随时间变化。相应地,称等式(2.13)和等式(2.14)中的两个随机过程分别为一阶非平稳随机过程和一阶平稳随机过程。在实际应用中,我们更希望信号的期望是常数值。但不可否认的是,在实际应用中更多的是非平稳随机过程。对于一阶非平稳随机过程,发展了专门的信号处理方法,例如第一种情况中的
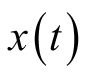 属于第4章所要介绍的一阶循环平稳过程。
属于第4章所要介绍的一阶循环平稳过程。
固定两个时刻
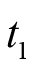 和
和
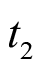 ,可以考察随机过程的二阶统计特征。随机过程
,可以考察随机过程的二阶统计特征。随机过程
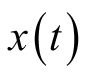 的自相关函数定义为
的自相关函数定义为
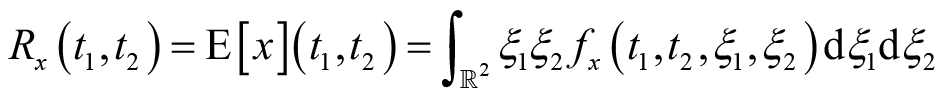 (2.15)
(2.15)
正如上述介绍的一阶平稳随机过程,我们希望随机过程的自相关函数与选择的具体时刻无关。相关函数中有两个变量,如果其数值与具体选择的时刻
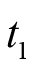 和
和
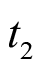 无关,那么就只依赖于两个时刻之间的差值
无关,那么就只依赖于两个时刻之间的差值
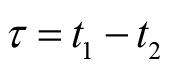 。满足该条件的随机过程包括概率密度函数
。满足该条件的随机过程包括概率密度函数
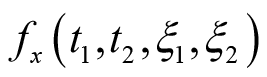 不随时间变化的随机过程。一般情况下,随机过程在任何两点的二维联合概率密度函数是不容易获得的,而随机过程的一阶和二阶统计量容易得到。因此,不方便从概率密度函数的角度判断信号的平稳性质。所以,有如下广义平稳随机过程的定义。
不随时间变化的随机过程。一般情况下,随机过程在任何两点的二维联合概率密度函数是不容易获得的,而随机过程的一阶和二阶统计量容易得到。因此,不方便从概率密度函数的角度判断信号的平稳性质。所以,有如下广义平稳随机过程的定义。
定义2
对于一个随机过程
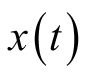 ,若
,若
(1)其数学期望为常数,
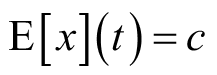 ;
;
(2)其自相关函数仅与时间间隔有关,
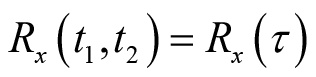 ;
;
(3)相关函数在零点的值有限,
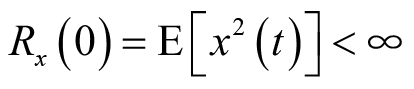 ,
,
则该随机过程为广义平稳随机过程(或二阶平稳随机过程、宽平稳随机过程)。
由该定义可知,二阶平稳随机过程一定是一个一阶平稳随机过程。
由此类推,可通过随机过程在3个或多个时刻的统计特性得到高阶平稳随机过程的概念。但是,它们在实际应用中较少出现,在此也不做介绍。现在介绍严平稳随机过程的概念。对于随机过程
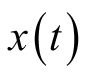 ,若其任意
,若其任意
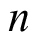 维概率密度函数不依赖具体的选择时刻
维概率密度函数不依赖具体的选择时刻
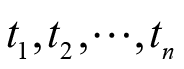 ,即
,即
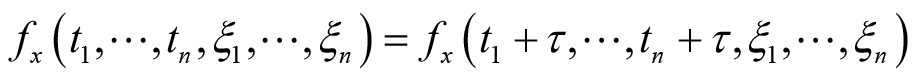 (2.16)
(2.16)
那么,该随机过程是严平稳的。正如二阶平稳随机过程的概念中介绍的,除少数像高斯随机过程的任意
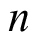 维概率密度函数可知,大部分随机过程的概率密度函数难以获得。所以在实际应用中较少涉及严平稳随机过程的概念。
维概率密度函数可知,大部分随机过程的概率密度函数难以获得。所以在实际应用中较少涉及严平稳随机过程的概念。
上述介绍随机过程的数字特征都是基于集合平均得到的。正如本节开始介绍的,随机过程是二维函数,在考察其特性的过程中,可以通过固定不同时刻,考察其统计规律;也可以通过固定不同样本,考察其样本随时间的变化规律。其实,这两种视角是可以殊途同归的。能够达到此效果的随机过程就是如下要介绍的遍历性过程。
类似于随机过程的数学期望和相关函数,定义随机过程的时间均值和时间相关函数分别为
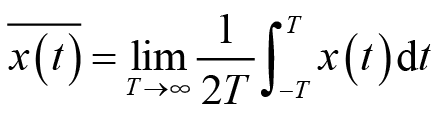 (2.17)
(2.17)
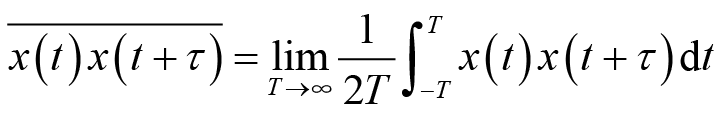 (2.18)
(2.18)
显然,
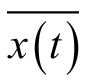 和
和
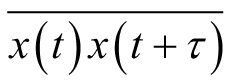 都具有随机性,其中,前者是与时间无关的一个随机变量,后者是只与
都具有随机性,其中,前者是与时间无关的一个随机变量,后者是只与
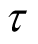 有关的一个随机过程。对于一个一阶平稳随机过程,其数学期望是一个常数,若其数学期望与时间均值以概率1相等,即
有关的一个随机过程。对于一个一阶平稳随机过程,其数学期望是一个常数,若其数学期望与时间均值以概率1相等,即
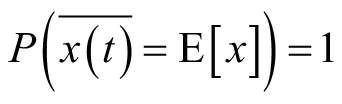 (2.19)
(2.19)
那么称该随机过程的均值具有遍历性。类似地,对于二阶平稳随机过程,若其相关函数与时间相关函数以概率1相等,即
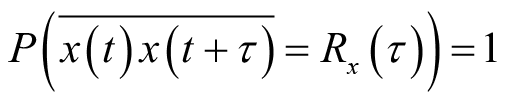 (2.20)
(2.20)
那么称该随机过程的自相关函数具有遍历性。若一个随机过程的均值和自相关函数都具有遍历性,那么称该随机过程具有遍历性。
遍历性又称各态历经性,是指随机过程的任何一个样本都经历了随机过程在集合维度所有可能的情况。遍历性的意义在于,在实际应用过程中,我们可以通过只观测一个样本和计算其在时间维度的平均来获得其统计性质。而观测一个样本比获取集合维度的特性要容易得多。
至此,我们已经介绍了从时间维度和集合维度考察信号的特性,并且介绍了这两种维度在遍历性随机过程中的等价性。为了更加深刻地描述和研究随机过程的性质,以下从频域的角度对信号展开分析。傅里叶变换是对随机过程的时间维度展开的,即对随机过程的样本进行傅里叶变换。由傅里叶变换的定义可知,信号需为能量型信号。但是,大部分随机过程的样本在整个时间轴上取值且值不为零。所以,随机过程的样本不是能量型信号,不能直接做傅里叶变换。可以通过对样本截断的方法,要求其在有限时间里的能量有限。定义信号的截断为
 (2.21)
(2.21)
该截断信号存在傅里叶变换且满足帕塞瓦尔定理,即
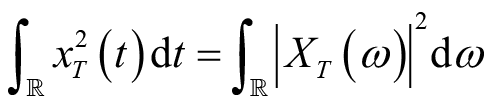 (2.22)
(2.22)
其中,
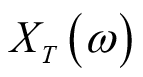 是
是
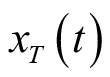 的傅里叶变换。为了消除截断时间
的傅里叶变换。为了消除截断时间
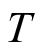 对信号的影响,应当令
对信号的影响,应当令
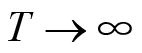 。受傅里叶变换存在性的限制,仅仅这样是不够的,还应把上述信号在时间上取平均,得到
。受傅里叶变换存在性的限制,仅仅这样是不够的,还应把上述信号在时间上取平均,得到
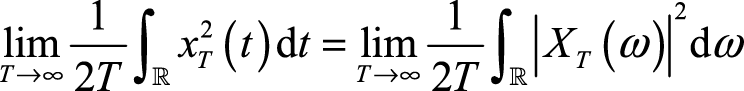 (2.23)
(2.23)
等式(2.23)左端的极限可表示为
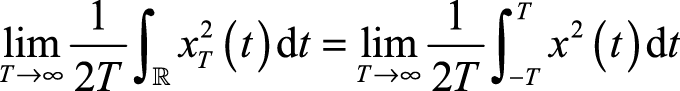 (2.24)
(2.24)
表示样本函数的平均功率;等式(2.23)右端可表示为
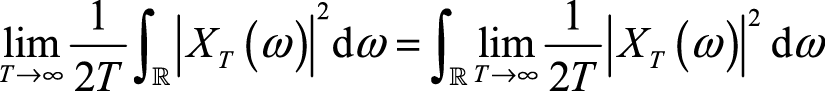 (2.25)
(2.25)
所以被积函数
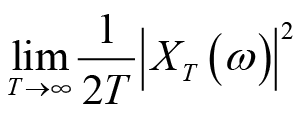 称为样本函数
称为样本函数
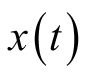 的功率谱密度。
的功率谱密度。
等式(2.23)~等式(2.25)的结论针对每个样本函数都成立,所以对整个随机过程也成立,当然,在此基础上求集合意义上的平均也成立。将等式(2.24)和等式(2.25)代入等式(2.23)中,并对等式两端同时取数学期望,可得
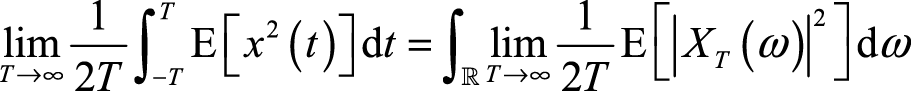 (2.26)
(2.26)
被积函数
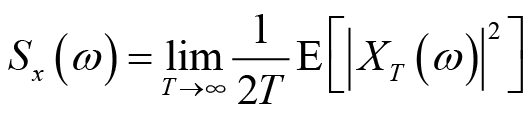 称为随机过程的功率谱密度。
称为随机过程的功率谱密度。
功率谱密度从频域的角度给出了刻画随机过程的二阶统计特征,与时域中刻画随机过程特征的相关函数互为补充。一个自然的问题是:这两个统计量之间是否存在一定的联系?以下回答这个问题。从功率谱密度函数的定义式出发,可得
 (2.27)
(2.27)
相关函数反映了时域里两个信号之间的关系,所以我们用时域里的信号表示上述频域中的信号
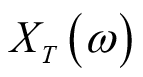 ,可得
,可得
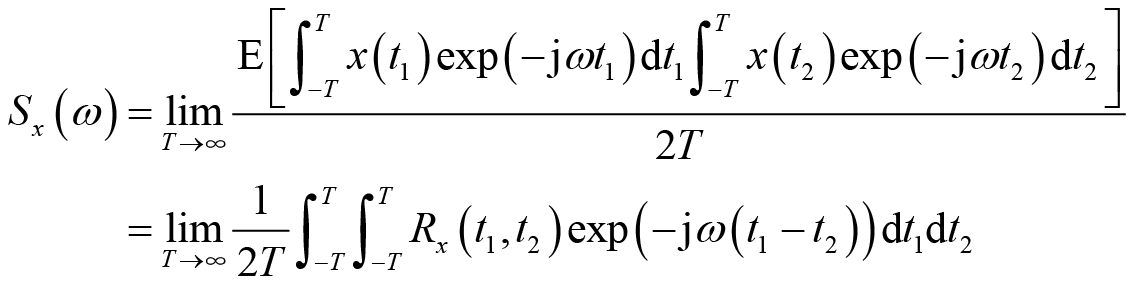 (2.28)
(2.28)
令
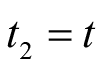 ,
,
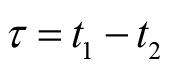 ,则这两个变量的取值范围也相应变化为
,则这两个变量的取值范围也相应变化为
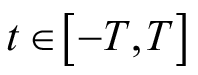 和
和
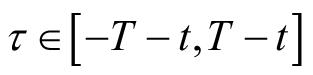 。将新的变量和其取值范围代入
。将新的变量和其取值范围代入
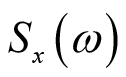 的表达式中,可得
[4]
的表达式中,可得
[4]
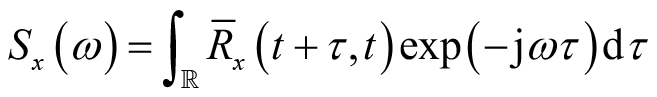 (2.29)
(2.29)
等式(2.29)中所表示的功率谱与相关函数之间的关系不限制信号的平稳性。对于宽平稳随机过程,积分中的相关函数
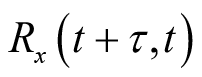 与时间变量
与时间变量
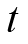 无关,可表示为
无关,可表示为
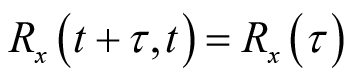 ,所以对时间平均后仍为
,所以对时间平均后仍为
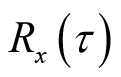 。此时,等式(2.29)中表示的功率谱密度与相关函数之间的关系简化为
。此时,等式(2.29)中表示的功率谱密度与相关函数之间的关系简化为
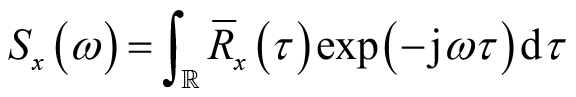 (2.30)
(2.30)
这就是著名的维纳-辛钦定理。此等式关系也为平稳随机过程的功率谱密度求解提供了简单方法。
对于非平稳随机过程,可通过对其相关函数的时间变量求时间平均,再对其结果求关于时延变量的傅里叶变换得到。这种对相关函数的时间变量求平均的方法忽略了相关函数随时间变化的特征。若需考察相关函数的谱随时间的变化特征,则可对相关函数的时延变量求傅里叶变换并观察其随时间的变化规律。另一种方法是直接考察非平稳随机过程的相关函数在时间维度的变化规律,例如,第4章介绍的循环平稳随机过程的相关函数
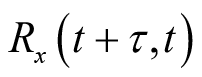 随时间
随时间
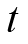 周期性变化,此时,可以通过傅里叶级数展开的方法考察相关函数的特征。
周期性变化,此时,可以通过傅里叶级数展开的方法考察相关函数的特征。
随机信号经过线性时不变系统后的输出依然具有随机性,这里介绍输入、输出信号统计量之间的关系。随机过程
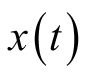 经过冲激响应为
经过冲激响应为
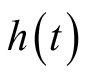 的线性时不变系统的输出记为
的线性时不变系统的输出记为
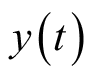 ,其流程图如图2.1所示。
,其流程图如图2.1所示。
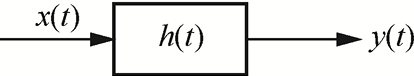
图2.1 信号经过线性时不变系统
由系统的线性和时不变性可知,输出信号可表示为输入信号与系统冲激响应的卷积,即
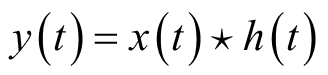 (2.31)
(2.31)
输出
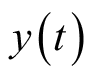 的数学期望为
的数学期望为
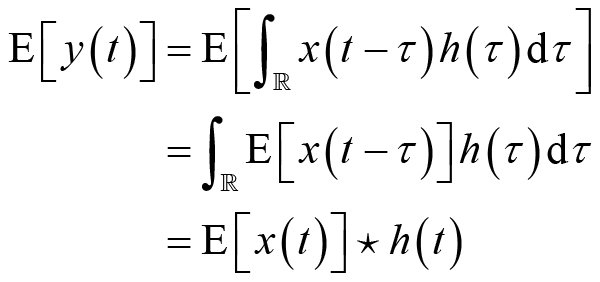 (2.32)
(2.32)
由此规律可知,无须输出信号在每个时刻的概率分布函数,仅由输出信号的一阶统计特征和系统的冲激响应就能得到输出信号的一阶统计特征。特别地,当输入信号是一阶平稳随机过程,即
 为常数时,输出信号的数学期望也是一个常数,即输出信号也是一阶平稳的。这也说明线性时不变系统保持随机过程的一阶平稳性。
为常数时,输出信号的数学期望也是一个常数,即输出信号也是一阶平稳的。这也说明线性时不变系统保持随机过程的一阶平稳性。
输出信号
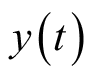 与输入信号的互相关和
与输入信号的互相关和
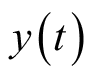 的自相关函数分别为
的自相关函数分别为
 (2.33)
(2.33)
和
 (2.34)
(2.34)
所以输出信号相关函数与输出信号的自相关函数之间的关系为
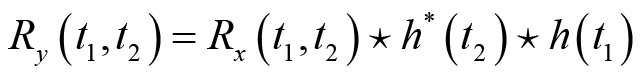 (2.35)
(2.35)
由此可知,输出信号的自相关可以通过输出信号的自相关函数和系统的冲激响应得到,而不需要输出信号的二维概率分布函数。特别地,当输入信号是宽平稳随机过程时,等式(2.33)、等式(2.34)和等式(2.35)所表示的输出信号与输入信号的互相关函数和输出的自相关函数分别简化为
 (2.36)
(2.36)
 (2.37)
(2.37)
和
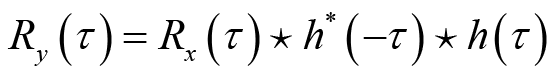 (2.38)
(2.38)
由此可知,线性时不变系统保持输入信号的二阶平稳性质。
由功率谱密度函数的定义和上述相关函数之间的关系可得输入和输出信号功率谱之间的关系,具体表示如下
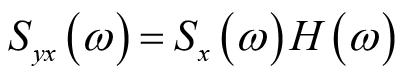 (2.39)
(2.39)
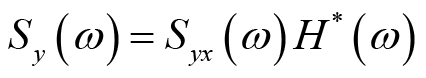 (2.40)
(2.40)
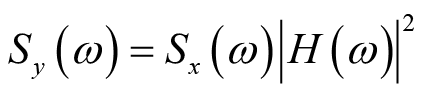 (2.41)
(2.41)
这些相关函数和功率谱之间的关系为匹配滤波器设计、系统辨识等应用提供了基本工具和原理。