




傅里叶变换一般指连续信号的傅里叶变换,也可以是傅里叶变换、傅里叶级数、离散时间傅里叶变换、离散傅里叶变换的统称。根据信号类型的不同,傅里叶变换有不同的名称,如表2.1所示。
表2.1 傅里叶变换的名称

连续信号的傅里叶变换定义如下。
定义1
确定性信号
 的傅里叶变换定义为
的傅里叶变换定义为
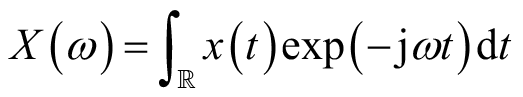 (2.1)
(2.1)
其中,
 是实数集,
是实数集,
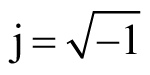 是复数单位,
是复数单位,
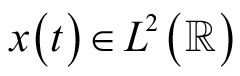 表示
表示
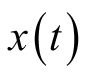 是
是
 上的平方可积信号,也指物理上的能量型信号;
上的平方可积信号,也指物理上的能量型信号;
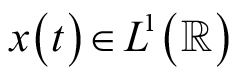 保证了
保证了
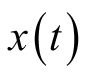 傅里叶变换的存在性。
傅里叶变换的存在性。
相应地,逆傅里叶变换表示为
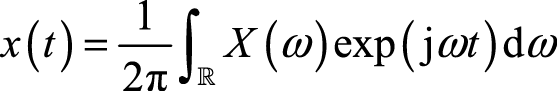 (2.2)
(2.2)
逆变换给出了一种信号在复正弦基函数
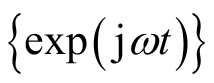 上的分解形式,其中每个复正弦基函数的“强度”为
上的分解形式,其中每个复正弦基函数的“强度”为
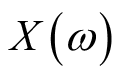 。按照此理解,小波变换、分数傅里叶变换等都是在不同基函数上的分解。这里也可以发现,当信号
。按照此理解,小波变换、分数傅里叶变换等都是在不同基函数上的分解。这里也可以发现,当信号
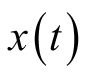 可表示为有限个复正弦函数的加和时,其傅里叶分解有简洁的表示形式。但如果在以线性调频函数
可表示为有限个复正弦函数的加和时,其傅里叶分解有简洁的表示形式。但如果在以线性调频函数
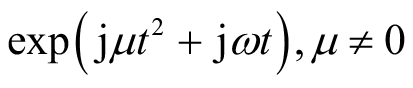 为基函数上展开时,需要用无穷多个基函数逼近。这里就引申出“匹配”的概念,即信号类型与变换基函数的类型相一致时,在这种基函数上的展开有最简洁的形式。这对于数据处理和压缩都很有帮助。当然,也存在没有固定基函数的变换,例如,经验模态分解和奇异谱分析等,这类变换也可以看作信号自适应的变换。本书关注的是有固定基函数的变换。
为基函数上展开时,需要用无穷多个基函数逼近。这里就引申出“匹配”的概念,即信号类型与变换基函数的类型相一致时,在这种基函数上的展开有最简洁的形式。这对于数据处理和压缩都很有帮助。当然,也存在没有固定基函数的变换,例如,经验模态分解和奇异谱分析等,这类变换也可以看作信号自适应的变换。本书关注的是有固定基函数的变换。
上述定义的正逆傅里叶变换有系数
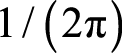 的差别,因此也有对称形式的傅里叶变换定义
的差别,因此也有对称形式的傅里叶变换定义
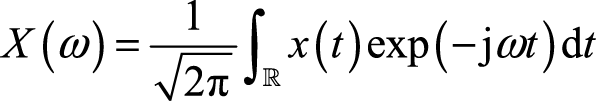 (2.3)
(2.3)
相应地,其逆变换表示为
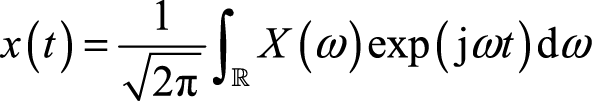 (2.4)
(2.4)
以下介绍的分数傅里叶变换和线性正则变换都是这种形式定义的傅里叶变换的广义形式。
除可逆性,傅里叶变换还有许多优良性质,列举如下。
(1)共轭性质:令
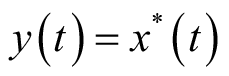 ,则有
,则有
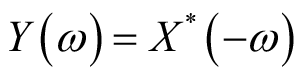 ,其中,
,其中,
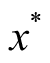 表示
表示
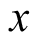 的共轭。
的共轭。
(2)平移性质:令
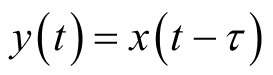 ,则有
,则有
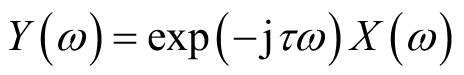 。
。
(3)调制性质:令
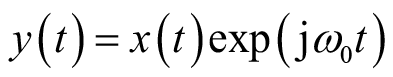 ,则有
,则有
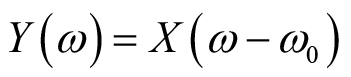
(4)微分性质:令
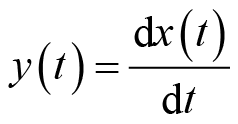 ,则有
,则有
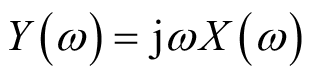 ,其中
,其中
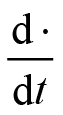 是微分算子。
是微分算子。
(5)帕塞瓦尔定理:
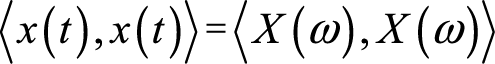 ,其中,
,其中,
 表示内积运算。
表示内积运算。
(6)卷积定理:
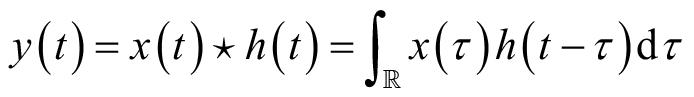 ,其中,
,其中,
 是卷积运算算子。在卷积运算中,函数
是卷积运算算子。在卷积运算中,函数
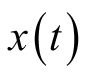 和
和
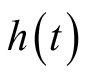 的位置可互换。卷积运算可表示线性时不变系统输入输出之间的关系,此时,
的位置可互换。卷积运算可表示线性时不变系统输入输出之间的关系,此时,
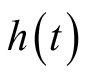 为系统的冲激响应;卷积算子还可表示两个随机变量和的概率密度函数,此时,
为系统的冲激响应;卷积算子还可表示两个随机变量和的概率密度函数,此时,
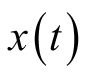 和
和
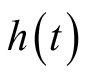 分别表示两个相加的随机变量的概率密度函数。卷积神经网络中所利用的卷积运算其实是信号处理中的相关运算。
分别表示两个相加的随机变量的概率密度函数。卷积神经网络中所利用的卷积运算其实是信号处理中的相关运算。
卷积运算的频域表征为:
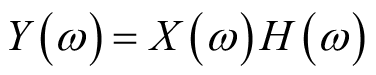 (2.5)
(2.5)
该定理使频域乘性滤波器的设计成为可能,可帮助快速实现卷积神经网络。
表2.2中列举了一些常见函数的傅里叶变换。
表2.2 常见函数的傅里叶变换

傅里叶变换在工程领域的广泛应用得益于快速傅里叶变换的提出和发展。通过快速傅里叶变换,一个
N
点序列的傅里叶变换的计算复杂度可从
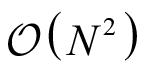 降低到
降低到
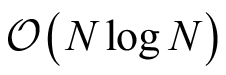 。
。
扩展: 傅里叶变换不仅可以提供信号的频域表征,也可以帮助求解微分方程,还可以用于深度学习的卷积神经网络算法中。调和分析作为现代数学分析的代表,正是从傅里叶变换和傅里叶级数发展起来的。
傅里叶变换为信号分析提供了除时域的另一个视角,同时也为线性时不变系统的分析和处理提供了新工具。线性时不变性是很多物理系统所具备的性质。为了充分利用系统的线性和时不变性,这里首先对离散信号进行分析,再利用求极限的思想拓展到连续信号。
任意一个序列
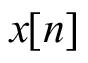 都可以表示为移位的单位脉冲序列
都可以表示为移位的单位脉冲序列
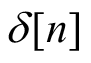 的线性组合,即
的线性组合,即
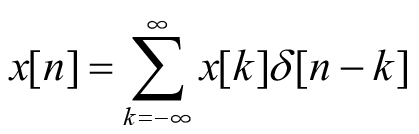 (2.6)
(2.6)
记
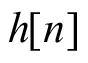 为线性时不变系统对单位脉冲
为线性时不变系统对单位脉冲
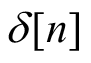 的响应,则利用系统的时不变性可知,对于单位脉冲的移位
的响应,则利用系统的时不变性可知,对于单位脉冲的移位
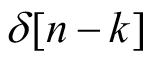 的系统响应为
的系统响应为
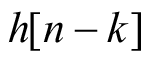 。利用系统的线性和时不变性可知,对于输入为
。利用系统的线性和时不变性可知,对于输入为
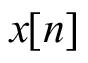 的系统的输出为
的系统的输出为
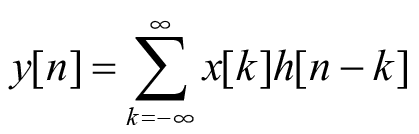 (2.7)
(2.7)
这正是离散卷积的表示。对于连续信号
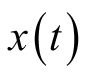 ,可由无穷求和逼近
,可由无穷求和逼近
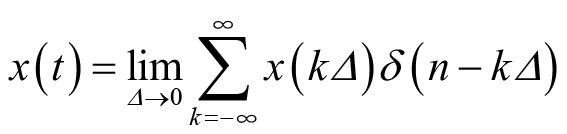 (2.8)
(2.8)
其通过线性时变系统后的输出为
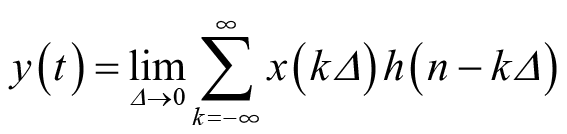 (2.9)
(2.9)
随着
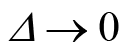 ,等式(2.8)和等式(2.9)所表示的极限可分别用积分表示为
,等式(2.8)和等式(2.9)所表示的极限可分别用积分表示为
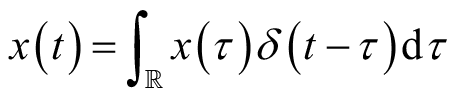 (2.10)
(2.10)
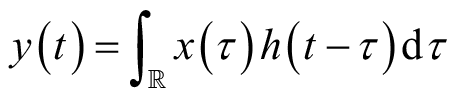 (2.11)
(2.11)
这正是连续函数的卷积表示。由傅里叶变换的卷积定理可知,信号经过线性时变系统后的输出可由时域里的卷积计算得到,也可由频域里的乘积运算得到。鉴于快速傅里叶变换的发展,在实际计算过程中会更多地用到第二种方法。