2.1 格理论基础

格（Lattice） L 指在 n 维欧几里得空间R ⁿ 中由无限个离散的点构成的具有周期性的数学结构。如果给定 n 个线性无关的向量 b ₁ ， b ₂ ，…， b _n ∈R ⁿ ，由它们可以生成一个格 L ，则可以称 b ₁ ， b ₂ ，…， b _n ∈R ⁿ 为 L 的一组基（Basis），且这组基向量的任意线性组合的集合形成了整个 L ：

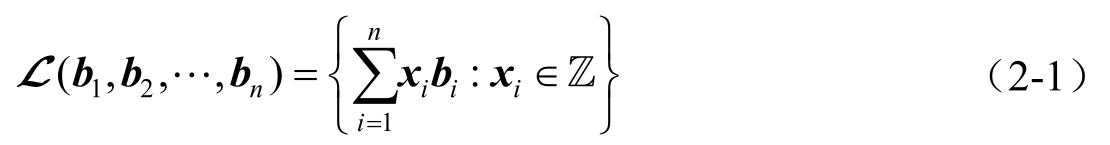
这也被称为标准格（Standard Lattice）。格的基并不是唯一的，通过使用线性代数中的基变更运算（Change of Basis），很容易计算得到一组新的基向量。一个简单的二维格和它对应的两种可能的基向量如图2-1所示。因此，从数学的角度而言， L 是R ⁿ 中离散加法子群（Discrete Additive Subgroup）。

理想格（Ideal Lattice）则定义在整数多项式环 R _q =Z _q [ x ]/（ f （ x ））上。其中，Z表示整数集合，正整数 q 为模数， f （ x ）= x ⁿ + f _n x ^{n -1} +…+ f ₁ ∈ Z[ x ]为不可约的分圆多项式（Cyclotomic Polynomial），且 R _q 中所有多项式需要对 f （ x ）进行取模运算，其系数都需要对 q 进行取模运算。并且，当 f （ x ）是一个 n 阶首项系数为1的（Monic）不可约多项式时， R _q =Z _q [ x ]/（ f （ x ））包括次数项不大于 n -1阶的多项式。例如，在 n 是2的幂时， R _q =Z _q [ x ]/（ x ⁿ +1）是一个理想格；然而， R _q =Z _q [ x ]/（ x ⁿ -1）不是一个理想格，这是因为 x ⁿ -1是一个可约多项式。 6EcB/Pm8rZdborBUlqwWL8RCVNwX5NG8P2T9rWZoVGgttFKAca/Do8JsgV7vtj1L