




2008年国际金融危机爆发以来,全球政府债务规模急剧上升,引起各界广泛关注。此前理论界对债务问题的研究主要集中在外债的影响上,危机之后研究重点开始转向政府债务对经济的影响。尤其是在Rogoff和Reinhart发表论文《债务时代的增长》( Growth in a Time of Debt )后,政府债务与经济增长之间的关系获得更大范围的关注。Rogoff和Reinhart(2010a)通过对44个国家近200年政府债务与经济增长数据进行研究,发现当政府债务占GDP的比重超过90%后经济增速将明显下降。此外,欧盟也将政府债务占GDP比重的60%设为警示值。
近年来,在全球经济增长乏力、货币政策对经济刺激作用普遍减弱的情况下,现代货币理论(MMT)兴起。MMT认为若政府能够以本币借债,就不必担心债务偿还的问题,能够增加财政收入,因此“内债不是债”,因为政府总能够通过印钞来解决债务问题,财政扩张的空间很大。MMT理论不乏反对者,美联储主席鲍威尔及保罗·克鲁格曼等都对这一理论持反对态度,他们担心政府通过债务货币化无限举债将带来恶性通胀,反而对经济造成损害。争论的焦点在于债务是否存在边界,而讨论政府债务约束问题,本质上就是探讨政府债务与经济增长的关系,即政府债务对经济增长的影响是否存在阈值,使得政府债务规模的扩张对经济起到先促进后抑制的作用。本章对理论文献进行梳理,试图厘清政府债务对经济增长影响的传导机制,并对债务是否存在边界的问题进行实证研究。
不少学者已就政府债务与经济增长的关系进行了研究。Elmendorf和Mankiw(1999)、Corden(1988)等建立不同理论模型探讨这一问题,Reinhart和Rogoff(2010a)等则通过对不同经济体、不同时间段数据使用不同估计方法进行实证分析。本部分我们将从理论研究和实证分析的角度分别对这些研究成果进行回顾。
债务扩张短期内能够促进经济增长是理论界的共识。在债务水平较低时,债务扩张能够刺激总需求,从而促进经济增长。Elmendorf和Mankiw(1999)认为,短期内价格和工资存在粘性,总需求增加会使总产出增加。具体来看,在政府支出保持不变的情况下,减税会增加政府债务,减税能够提高居民可支配收入,从而刺激总需求,最终使总产出增加。多数文献都将政府债务增加对经济增长的正向作用归因于短期的扩张性财政政策。
不过若政府债务水平过高,则对经济增长有抑制作用。Elmendorf和Mankiw(1999)认为,在长期价格和工资具有弹性,此时财政赤字会挤出投资,对长期经济增长具有负面影响。还有许多研究通过建立其他理论分析框架,来探讨政府债务对经济增长的负面影响。例如,Barro(1979)认为在债务高企的情况下,政府可能通过提高税收的方式来维持债务可持续性,而由此导致的高通胀预期对经济增长有负向作用。克鲁格曼(Krugman,1988)认为,当债务超过政府偿还能力时,一是投资回报会因边际税收增加而减少,导致投资减少;二是在高债务水平下,政府可能会在偿还债务上花费更多,相应地政府支出中用于投资的部分则会减少。总的来说,政府债务可能会通过影响投资总量和投资效率(包括政府部门的投资和私人部门的投资)而影响经济增长。Corden(1988)认为,在政府债务水平很高的情况下,政府会在降低债务规模的前提下来制定政策,在此约束下很难实施最优的宏观政策,这会降低投资效率,从而对经济增长产生负面影响。
研究表明,政府债务高企带来的不稳定性会影响长期经济增长。Serven(1997)认为,一国投资规模取决于投资环境,即在该国进行投资的潜在风险和回报,而不确定性增加会使某些觉察到风险的投资者减少投资。此外,不确定性会导致投资资源错配,投资者会更倾向于投资能够快速回报的领域,而不是那些更需要长期资金支持的领域,资源错配会降低整体资本积累的效率。
研究还表明,政府债务对经济增长的影响是非线性的。Cohen(1991,1992)认为,资本积累在驱动经济增长中扮演了至关重要的角色,政府债务较低的国家由于其风险较低,可以从本国和国际市场中获得更多的资本用于投资。但是随着借款增加,经济增速放缓可能与偿债负担显著增大有关。高债务水平会增加税负负担,如果经济增长不足以偿还其债务,政府就需要进一步举债。这些负面影响会降低投资回报率,减少投资,导致经济增速继续下降,形成两者之间的相互强化和放大。
“债台高筑”(Debt Overhang)理论表明,高水平债务会让投资者形成未来高税收扭曲的预期,导致国内外投资减少,从而影响资本形成(Krugman,1988;Sachs,1989),这一理论的代表是债务拉弗曲线(Debt Laffer Curve,Pattillo、Poirson和Ricci,2002)。债务拉弗曲线呈现出“倒U形”,在曲线的左边,随着债务还本付息压力增大,实际的债务偿还也在增加;但在曲线的右边,债务的增加可能使预期的债务偿还减少,高债务存量更倾向于与低概率债务清偿相关。曲线的转折点表明超过某一程度的债务水平可能会对投资和生产效率造成负面影响。Checherita-Westphal、Hallett和Rother(2012)认为存在最优政府债务规模(最大化经济增速的政府债务规模),其由最大化经济增速的资本存量产出弹性所决定。
研究政府债务与经济增长的关系还需重视国家间的异质性。Panizza和Presbitero(2013)对研究发达国家政府债务与经济增长的文献进行综合分析,发现这些文献计算出的非线性关系阈值并不稳定,结果会随着样本选择和模型设定发生改变。他们认为政府债务和经济增长的关系可能随着国家和时间而改变,可能并不存在一个不变的阈值,使债务由“好”变“坏”。美洲开发银行(2006)也同样提出要重视国家间的异质性,认为债务对经济增长的影响渠道取决于政府债务的结构、组成以及政府债务累积的方式和原因。
针对发达经济体的研究表明,政府债务对经济增长的作用是非线性的。Checherita-Westphal和Rother(2012)通过分析12个欧元区经济体1970年之后近40年的数据,发现政府债务与经济增长之间呈现“倒U形”关系,且政府债务对经济增长的阈值为90%~100%;Mencinger、Aristovnik和Verbic(2014)研究了欧盟25个国家,通过将样本分为全部成员(在1980—1994年加入欧盟)和新成员(在1995—2010年加入欧盟),他们发现对全部成员来说债务占GDP的比重阈值为80%~90%,而新成员的阈值则为50%~54%。当然也有学者有不同的看法,例如Minea和Parent(2012)运用PSTR模型发现债务/GDP在90%~115%时,政府债务与经济增长之间是负向关系;而当债务/GDP超过115%,政府债务对经济增长又呈现促进作用;Panizza和Presbitero(2014)认为政府债务与经济增长之间并不存在明显的因果关系。
对发展中经济体及混合样本的研究得出了与发达经济体相近的结论。Nguyen、Clements和Bhattacharya(2003)对55个低收入水平国家1970年至1999年的数据进行研究发现,如果外债/GDP低于50%(或者外债/GDP为20%~25%),债务增加会促进经济增长;而当债务水平超过这一阈值时,经济增速则会放缓。Pattillo、Poirson和Ricci(2002)使用93个发展中经济体1969年至1998年的面板数据,通过不同估计方法发现,当债务/GDP在35%~40%及债务占出口的比重在160%~170%时,债务对经济增长的影响为负。
也有学者使用发展中经济体和发达经济体的混合样本进行研究,Reinhart和Rogoff(2010a)通过研究44个经济体近200年的数据,将政府债务/GDP分为四组进行研究,分别是低于30%、30%~60%、60%~90%和超过90%,发现当政府债务/GDP超过90%时,政府债务对经济增长有负向作用。Kumar和Woo(2010)研究了38个发达经济体和新兴市场经济体1970—2007年将近40年的面板数据,结果与Reinhart和Rogoff(2010)一致,发现政府债务/GDP的阈值在90%左右。Eberhardt和Presbitero(2015)通过对118个混合经济体样本1960—2012年的面板数据进行研究,发现政府债务与长期经济增长之间存在负向关系,但在不同的经济体两者的关系可能不同,应注意经济体的异质性。
针对中国的情况,刘溶沧和马拴友(2001)发现赤字和国债规模并未产生挤出效应:一是财政赤字并未导致利率水平上升;二是财政投资也并未挤出私人投资。他们认为政府债务增加对经济增长的影响取决于其用途:当赤字、国债用于公共投资时对经济增长有正向作用,若用于其他经常性支出则对经济增长有负向作用。
已有文献对政府债务和经济增长之间的关系做了大量研究,但仍存在一定的争议和不足。一是关于政府债务增加对经济增长的影响是否为先促进经济增长、超过阈值后抑制经济增长仍存在争议。Herndon、Ash和Pollin(2014)使用Reinhart和Rogoff(2010a和2010b)的数据,指出其存在计算错误、选择性地排除某些可得数据以及不合理地给予某些统计数据权重三方面问题,导致错误地描述了第二次世界大战后20个发达经济体政府债务与经济增长之间的关系。他们在修正数据后计算出政府债务/GDP为90%以上经济体其GDP增长率实际为2.2%,而并不是原来文献中的-0.1%。二是没有考虑到政府债务波动对经济增长的影响。政府债务波动体现了政府运用财政政策进行逆周期调节经济的情况,特别是在主要发达经济体“非常规货币政策”常规化的背景下财政政策的作用愈发凸显。
鉴于现有研究存在的争议和不足,我们试图从以下两个方面提供一些边际贡献:一是综合现有文献对政府债务影响经济增长的研究,构建统一的分析框架,阐释政府债务在短期和长期对经济增长的不同影响及传导机制;二是通过引入新的政府债务波动项变量,研究政府财政调控对经济增长的影响,丰富关于政府债务与经济增长关系的研究。本章第二节对政府债务对经济增长的非线性影响机理进行分析,第三节在理论分析的基础上选择具有代表性的样本进行实证分析,然后根据研究结果对比分析中国政策情况,最后总结并提出政策建议。
债务融资对促进经济增长和提高生产效率不可或缺。债务随人类社会的发展自然演变,是经济发展的内在需要。在经济理论中,对专业化和分工所能起到的功效是少有的、没有争议的问题之一,一提起专业化和分工的增进就等于在说生产力的提高(盛洪,1992),而分工最大的特点就是迂回的生产方式。专业化分工程度提升表现为生产迂回度的深化,是在初始生产与最终消费之间的中间环节不断增加,流转路径不断延长。奥地利学派认为,生产过程中的重组和迂回是提高生产力的重要方式,迂回生产程度加深不仅需要使用更为专业的劳动力与更多的资本,且生产步骤的增多也增加了所需要的中间投入的数量。投资可以发展生产,因为投资可以加深生产的迂回程度,而投资的资金主要源自储蓄。总的来看,迂回生产是专业化分工过程中提高生产率的关键。而在迂回生产过程中,中间品生产者在获利之前进行的产品生产投入和产品创新投入,都由他人提供资金进行支持,由此就可能形成债务,因此债务对经济增长和提高生产效率不可或缺。当然债务积累过度意味着投资没有回报,从而反映出经济缺乏内生动力。
比较而言,政府债务较私人债务更值得关注。在社会运行过程中,个人、企业和政府等都会涉及借债问题,但私人部门债务和政府部门债务各有不同的特点。布坎南认为,私人部门借债和公共部门借债都是为应对当期的需要而取得未来支付额外购买力的经济行为,但二者存在差异:政府债务是通过增加纳税人的负担来偿还的,但私人部门不存在这种情况。对于私人部门而言,只要投资的边际收益大于借债的边际成本,就会产生相应的借款行为。特别是在需要大量长期资金投入的制造业,在生产过程中企业需要负债经营,且债务约束是相对硬性的,有市场化的自我调节机制。政府部门债务较私人部门债务软约束特征更明显,道德风险也更高。因此需要重点关注政府债务对经济增长的影响。
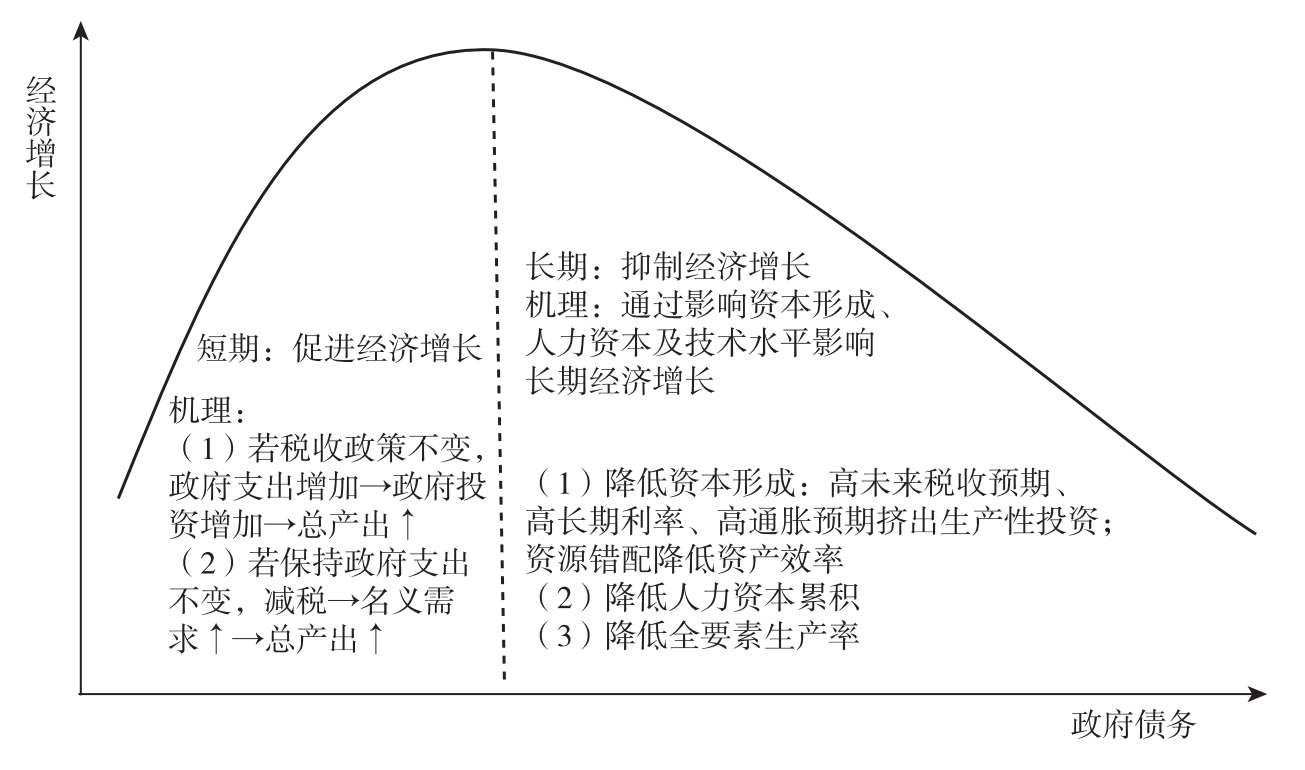
图3.1 政府债务影响经济增长机理示意图
(数据来源:作者绘制)
一般来说,较低的政府债务能够促进经济增长,而当其超过某一阈值时,政府债务的增加就会抑制经济增长。政府债务可能在两种情况下扩张:一是在税负不变的情况下增加政府支出;二是保持政府支出不变的同时减税。如前文所述,迂回生产是专业化分工中提高生产率的关键,而投资则是加深迂回生产程度和发展生产的关键。政府通过举债进行基础设施建设以及投资于其他公共产品,可能提高社会福利并促进经济增长(刘溶沧和马拴友,2001)。对于第二种情况,若政府减税导致债务增加,也能够通过刺激需求对经济增长起到促进作用。例如,Elmendorf和Mankiw(1999)就从减税刺激需求的角度建立了短期债务和长期债务对经济增长影响的统一分析框架 [1] ,减税会提高居民可支配收入,进而刺激消费,增加对商品和服务的总需求。这意味着,由于短期内价格和工资具有粘性,总需求增加会导致总产出的增长,政府减税或者增加财政支出带来的政府债务增长,能够刺激经济增长。
过度政府债务的扩张对经济增长有抑制作用。政府债务累积到一定程度后会通过影响投资、人力资本和全要素生产率等经济增长因素降低长期经济增速。在讨论经济的长期增长问题时,主要有两类模型:一是新古典增长模型(Neoclassical Growth Model),即 Y=F ( K , L ),常用的柯布—道格拉斯形式为 Y = AK ∂ L 1-∂ ;二是内生增长模型(Endogenous Growth Model),即 Y=F ( K , L×E ),区别是将技术水平作为模型的内生变量。虽然政府债务并不在经典长期经济增长模型中,但有许多研究表明政府债务可能影响决定长期经济增长的三大要素,即资本形成( K )、人力资本( L )和全要素生产率( A )。
首先,过度的政府债务可能挤出政府部门与私人部门的生产性投资,并且降低投资效率,从而影响长期经济增长。在Elmendorf和Mankiw(1999)的分析框架下,减税带来的财政赤字会减少公共储蓄,由于私人部门储蓄增加不足以弥补公共部门储蓄减少,国民总储蓄会减少,本地投资和国外投资都下降,从而导致产出下降。具体来说,过高的政府债务可能通过以下三方面影响生产性投资,从而降低经济增长。
一是政府债务高企带来高税收预期(Barro,1979)。对投资者来说,政府债务过高可能直接扭曲投资:考虑到财政的可持续性,投资者会认为投资项目的收益会被征税以偿还之前的高债务,所以会减少当前投资(Krugman,1988)。例如,Dotsey(1994)建立动态均衡模型研究了在扭曲税收条件下政府预算的跨期均衡问题,表明在税收扭曲情况下私人部门将考虑未来税收负担变化,从而减少投资和产出。
二是政府债务过高带来较高的长期利率。高政府债务意味着未来风险上升,导致高长期利率(Gale和Orszag,2003;Baldacci和Kumar,2010),使投资成本上升,最终影响投资和产出。格林斯潘也认为财政赤字会影响长期利率从而对经济造成影响。政府债务能够影响货币政策,高债务的经济体更可能面对较高利率水平。虽然货币当局在短期内可以通过扩张性货币政策降低利率以减轻债务负担,但长期看实际利率不变并且会导致通胀和更高的名义利率。美联储前主席保罗·沃尔克、阿兰·格林斯潘都曾提示过二者之间存在的上述关系(Poirson、Ricci和Pattilo,2004)。
三是过高的政府债务可能带来高通胀预期(Barro,1995)。若政府债务过高,人们会认为政府将通过印钞来还债,即预期到未来会形成通货膨胀,这样就会调整现在的行为,从而抬升商品和服务价格,最终带来金融混乱和经济衰退(Cochrane,2011)。这也正是MMT反对者们所担忧的问题。
总的来说,高税收预期、高长期利率以及高通胀预期会减少私人部门的生产性投资,降低资本形成;而高债务带来的偿债压力又使政府部门在预算约束下减少生产性投资。高政府债务带来的风险导致投资领域的资源错配,资金更倾向于进入短期获得收益的领域,而较少投资需要长期资金的领域,因此不利于形成长期资本,降低投资效率(Serven,1997)。
其次,高政府债务可能通过减少人力资本累积而影响经济增长。一是高债务水平带来的偿债压力严重限制了低收入国家提供公共服务的能力,而教育就是国家应该提供的公共服务之一。二是教育也是一种投资决策,可能会受到高预期边际税率的影响(Pattillo、Poirson和Ricci,2004)。
最后,高政府债务可能会降低全要素生产率。高存量债务水平会阻碍政府在技术进步、有效利用资源方面的改革动力,而资源的错误配置会导致更低的生产效率(Pattillo、Poirson和Ricci,2004)。此外,部分政府部门和私人部门生产性投资用于投资研发(R&D),这部分投资被挤出会对经济增长产生长时间的负面影响(Elmeskov和Sutherland,2012)。
既有研究表明,政府债务对经济增长的作用是非线性的。图3.2展示了日本1876年至2016年政府债务和经济增长的情况。第二次世界大战后的1945年日本实际GDP降至1944年的一半,政府债务/GDP也由1944年的204%下降至56%。战后二十余年里日本政府债务/GDP稳定在10%左右,同时日本经济持续快速增长。1976年以后,政府债务/GDP开始快速上升,同时日本经济增速回落到5%以下,增速出现负增长。
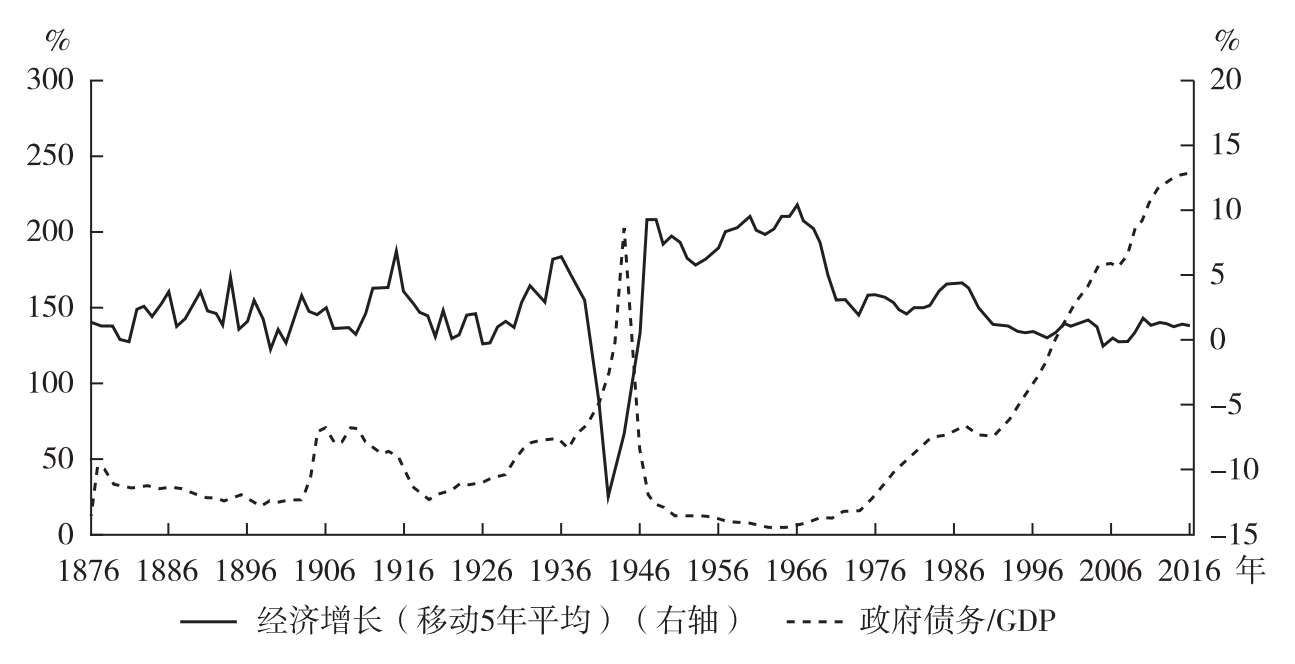
图3.2 日本1876—2016年政府债务占GDP的比重与经济增长
(数据来源:www.macrohistory.net,经作者计算)
图3.3展示了过去140余年里日本政府债务/GDP与经济增长之间的关系,可以发现债务率在100%~250%区间时,对应的经济增长不超过2%
 ,而在0~100%的债务区间时,平均经济增速则明显较高。日本政府债务和经济增长之间呈现出较为明显的非线性关系,低政府债务水平与较高的经济增速相对应,而高政府债务水平与较低的经济增速相互交织。
,而在0~100%的债务区间时,平均经济增速则明显较高。日本政府债务和经济增长之间呈现出较为明显的非线性关系,低政府债务水平与较高的经济增速相对应,而高政府债务水平与较低的经济增速相互交织。
为进一步观察政府债务与经济增长之间的关系,参考已有文献中常用的代表性经济体样本,同时考虑数据可获得性,我们选择了具有代表性的58个国家和地区1980年至2015年的政府债务/GDP与经济增长(使用实际GDP增速5年移动平均)数据进行研究分析(如图3.4所示)
 。在图3.4中,政府债务/GDP与经济增长关系的拟合线为“倒U形”抛物线,表明两者之间可能存在非线性关系,经济增速随着政府债务/GDP上升而出现先上升、后下降的变化特征。我们接着运用系统GMM的估计方法进行计量分析,验证了政府债务与经济增长之间存在显著的非线性关系。
。在图3.4中,政府债务/GDP与经济增长关系的拟合线为“倒U形”抛物线,表明两者之间可能存在非线性关系,经济增速随着政府债务/GDP上升而出现先上升、后下降的变化特征。我们接着运用系统GMM的估计方法进行计量分析,验证了政府债务与经济增长之间存在显著的非线性关系。
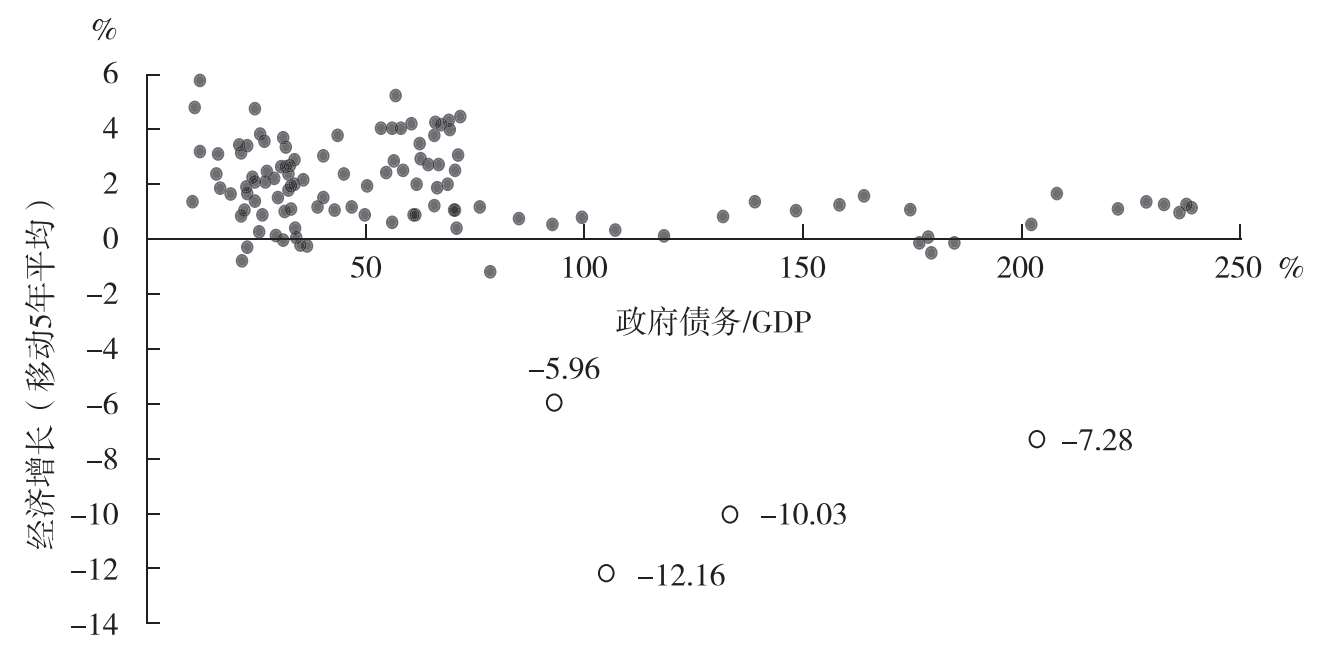
图3.3 日本政府债务/GDP与经济增长
(数据来源:www.macrohistory.net,经作者计算)
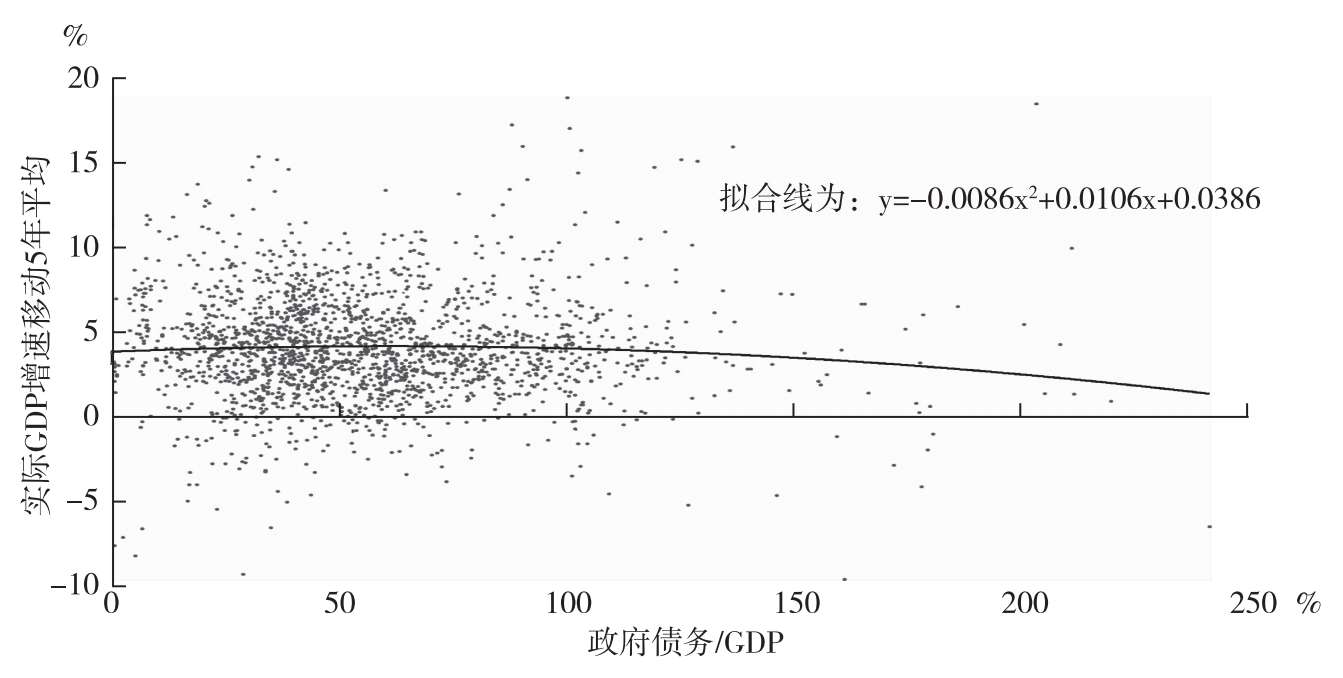
图3.4 58个国家和地区政府债务/GDP与经济增长之间的关系
本节选用上述58个经济体自1980年至2015年的面板数据进行实证研究。我们参照Cecchetti和Kharroubi(2012)研究私人部门信贷对经济增长影响的方法,在模型中加入政府债务水平的二次项,以检验政府债务与经济增长是否存在非线性关系。
同时,我们不仅考虑政府债务与经济增长之间的关系,还参考马勇和陈雨露(2017)研究金融杠杆波动对经济增长影响的方法,引入政府债务波动项,以考虑财政政策对经济增长的影响。参考ChecheritaWestphal和Rother(2012)等,选取可能对经济增长产生影响的因素作为控制变量,包括人均GDP对数以控制经济初始条件、贸易开放度、储蓄率、投资率和人力资本。
我们注意到有研究(Panizza和Presbitero,2014)质疑债务和经济增长之间的因果关系,即到底是因为在经济低增长时为刺激经济而形成高债务,还是高债务水平抑制了经济增长。例如在遭遇经济危机时,政府往往通过大量举债进行投资以刺激经济增长。为控制政府债务与经济增长之间的反向因果关系,我们参照Kumar和Woo(2010)、Checherita-Westphal和Rother(2012)的做法,用向前5年移动平均的实际GDP增长率表征经济增长。设定动态模型如下:
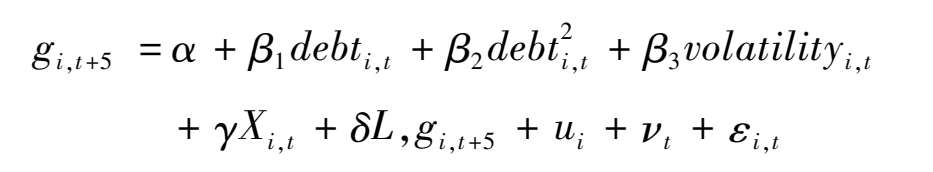
式中, g i,t+5 为实际GDP增速的5年移动平均; L , g i,t+5 表示 g i,t+5 的滞后一阶; debt i,t 为 i 国 t 时期的政府债务水平(政府债务/GDP); volatility i,t 表示政府债务波动,参考经典文献,用5年移动平均的标准差表示。 X i,t 为其他影响经济增长的因素,具体包括人力资本 schooling ,用15岁以上人口的平均受教育年限的对数表示;初始经济水平 lngdppc i,t ,用人均GDP的对数表示;贸易开放度 openness i,t ,用进出口总额占GDP的比例表示;资本形成率 invest i,t ,用资本形成总额占GDP的比例表示;储蓄率 saving i,t ,用总储蓄占GDP的比例表示。 μ i 为国家固定效应, ν t 为时间固定效应, ε i,t 为误差项。
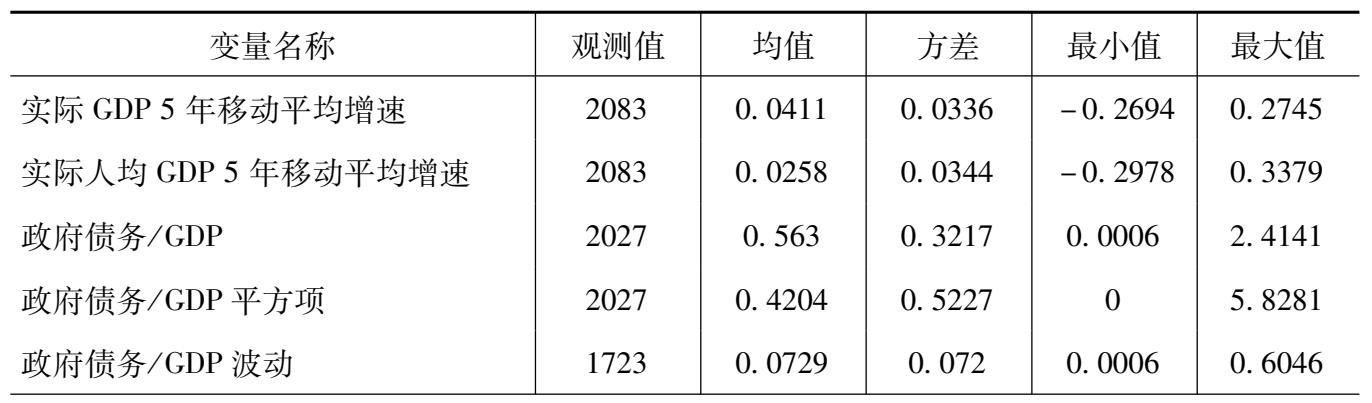
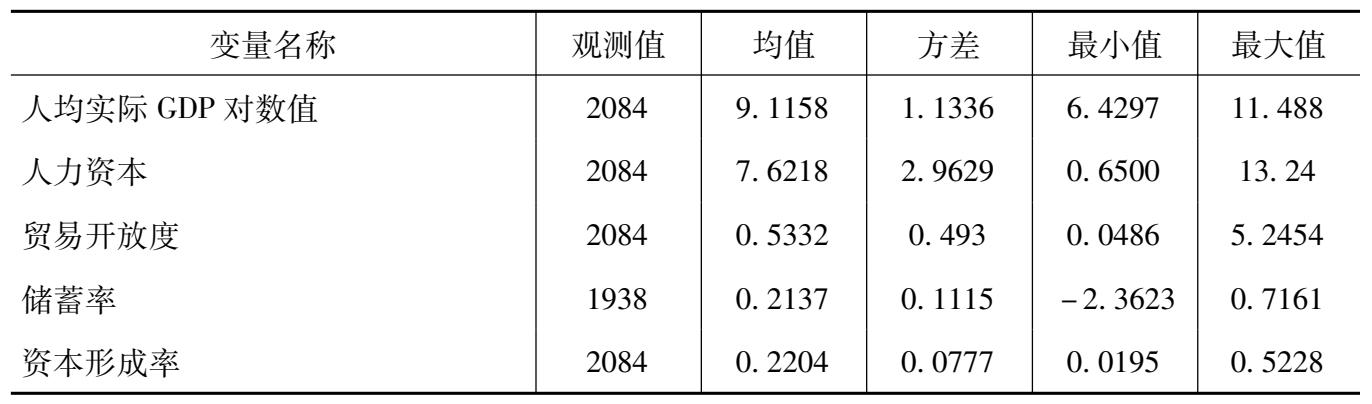
政府债务/GDP( debt )数据引自国际货币基金组织(IMF)的Historical Public Debt Database(HPDD)数据库;实际GDP、人口、进出口贸易总额、资本形成等数据来自佩恩表9.2版本(PWT9.2);15~65岁以上人口平均受教育水平来自Barro和Lee(2010)的数据库,该数据每5年更新一次,可以表征国家科技发展水平。研究样本的具体统计信息见表3.1。
表3.1 样本数据描述性统计
续表
在估计方法上,有学者运用包含不同国家和不同时段面板数据的固定效应模型或随机效应模型来研究政府债务与经济增长之间的关系;也有学者基于Hansen(1999)提出的非动态面板门限模型(Panel Threshold Model)和Gonzales、Terasvirta和Dijk(2005)改进的面板平滑转化回归模型(Panel Smooth Transition Regression Model)研究债务对经济增长影响的阈值效应(例如,Minea和Parent,2012);还有通过系统GMM模型研究金融杠杆与经济增长之间的关系(马勇和陈雨露,2017)。综合考虑上述三种估计方法的优缺点,我们选择系统GMM模型以克服内生性问题,提高估计结果的准确度。
计量模型的内生性问题会降低估计结果的准确性。虽然我们使用初始的政府债务作为主要解释变量、5年移动平均实际GDP增速作为被解释变量,可以在一定程度上避免债务与经济增长的反向因果关系;但这并没有完全解决模型的内生性问题,即不能解决政府债务和经济增长可能同时被其他因素影响这一问题。理论上工具变量法能够有效解决内生性问题,但在实际操作中却很难挑选到合适的工具变量,如果工具变量与解释变量相关性太弱,即存在弱工具变量问题,反而会使结果估计不准确。鉴于难以寻找关于初始政府债务水平和其他控制变量的工具变量,我们采用Arellano和Bover(1995)以及Blundell和Bond(1998)提出的系统GMM的估计方法来减少估计时的内生性问题,以提高估计的准确性。该方法选取解释变量的滞后项及差分项作为工具变量。系统GMM模型有一阶段和二阶段的差别,二阶段的系统GMM模型能够减少异方差和自相关的影响,所以选用二阶段系统GMM模型进行分析,并参照Windmeijer(2005)对系统GMM模型误差项的改进,得到稳健标准误。使用系统GMM方法需要进行两方面的检验:一是对残差进行序列相关性的Arellano-Bond检验,需要具有显著的一阶自相关AR(1)和不显著的二阶自相关AR(2);二是对工具变量的有效性进行Hansen检验。我们也在回归结果中报告AR(2)和Hansen检验的P值。
基于前文的理论分析及模型设定,本部分主要从实证角度考察政府债务及其波动对经济增长的影响。首先,以实际GDP增长率作为被解释变量,研究政府债务及其波动对经济增长的影响。其次,考虑到人均实际GDP增长率可以更好地从社会福利角度衡量经济增长情况,很多文献也同时研究实际GDP增长率和人均实际GDP增长率以作为对照,因此第二步以人均实际GDP增长率作为被解释变量,用同样的方法考察政府债务及其波动对经济增长的影响。这既可以从多角度考察政府债务对经济增长的影响,又能够检验以实际GDP增长率作为被解释变量模型的稳健性。再次,通过选取2008年国际金融危机之前的数据来排除金融危机的特殊影响,以同样的估计方式对前面的回归进行稳健性检验。最后,运用实证结果,对中国的情况进行分析。
1.基于实际GDP增长率的回归结果分析
我们选用系统GMM的估计方法,使用58个国家和地区1980—2015年的面板数据研究了政府债务与经济增长之间的关系。为清晰展示控制变量的引入过程及其对回归结果的影响,我们选择逐步加入控制变量的方式对回归结果进行呈现(模型1只考虑政府债务、政府债务的二次项以及政府债务波动对经济增长的影响。模型2至模型6在模型1的基础上依次分别加入初始经济水平、人力资本、贸易开放度、储蓄率和资本形成率等影响经济增长的其他控制变量)。具体回归结果如表3.2所示。所有模型均通过工具变量有效性的Hansen检验和二阶自相关AR(2)检验,表明模型的估计是有效的。
模型1只考虑政府债务( debt )、政府债务的二次项( debt 2 )以及政府债务波动( volatility )对经济增长的影响。当以实际经济增长率作为被解释变量时,政府债务( debt )、政府债务的二次项( debt 2 )以及政府债务波动( volatility )都在1%的置信水平下显著,系数的符号分别为正、负、正。
由此可得出以下结论:
第一,政府债务( debt )的系数符号为正,而其二次项( debt 2 )的系数符号为负,表明政府债务对经济增长的影响是非线性的,呈现出“倒U形”关系。随着政府债务/GDP的提高,经济增速会先上升后下降,存在拐点。
第二,模型1计算出“倒U形”拐点(即阈值)为83%[- β 1 /2 β 2 =-0.2414/2×(-0.1455)]。这表明当政府债务率低于83%时,政府债务增长对经济增长有促进作用;而当政府债务率高于83%时,政府债务增加会对经济增长产生抑制作用。
在研究政府债务与经济增长的关系时,需要注意国家间的异质性。Pannizza和Presbitero(2013)认为政府债务和经济增长的关系可能因不同国家和时间而改变,非线性关系的阈值是不稳定的。国家经济发展水平各异、金融发达程度不同、政府债务积累的方式和原因不同,导致各个国家承担政府债务的能力不同。我们的实证分析发现政府债务与经济增长关系变化的阈值是政府债务率为83%,虽然分国别看情况可能更复杂,存在异质性,但这一实证结果仍具有基准参考性价值。
第三,政府债务波动(volatility)系数符号为正,表明政府债务波动对经济运行可能有稳定作用。这与政府债务本身性质有关,与私人部门债务具有顺周期性不同,政府债务与财政政策运用联系在一起,往往具有逆周期调节功能。
模型2至模型6分别依次加入了初始经济水平lngdppc、人力资本schooling、贸易开放度openness、储蓄率saving和资本形成率invest等变量。加入这些控制变量后,政府债务(debt)、政府债务的二次项(debt 2 )以及政府债务波动(volatility)的符号并未发生改变,并且也至少在10%的置信水平下显著,表明模型估计是稳健的。
从其余控制变量来看,初始经济水平lngdppc的系数为负,表明初始经济水平越高的国家经济增长一般越缓慢;人力资本schooling系数为正,表明15岁以上人口平均受教育年限越高,对经济增长的促进作用越强;贸易开放度openness的系数为正,表明贸易越开放的国家经济增速越快;储蓄率saving和资本形成率invest的符号虽然不显著,但符号均为正,表明其对经济增长也有促进作用。这些控制变量系数符合直觉和逻辑,且整体上比较显著。
模型2至模型6在控制除政府债务(debt)、政府债务的二次项(debt 2 )以及政府债务波动(volatility)的情况下,计算出政府债务与经济增长作用关系变化的阈值分别为83.0%、89.4%、94.1%、85.9%、94.1%和104.8%。总体看,阈值在80%~105%之间。这一结果也与Rogoff和Reinhart(2010)等学者估算基本一致。
表3.2 政府债务对经济增长影响回归结果(1980—2015年)(实际GDP增速)
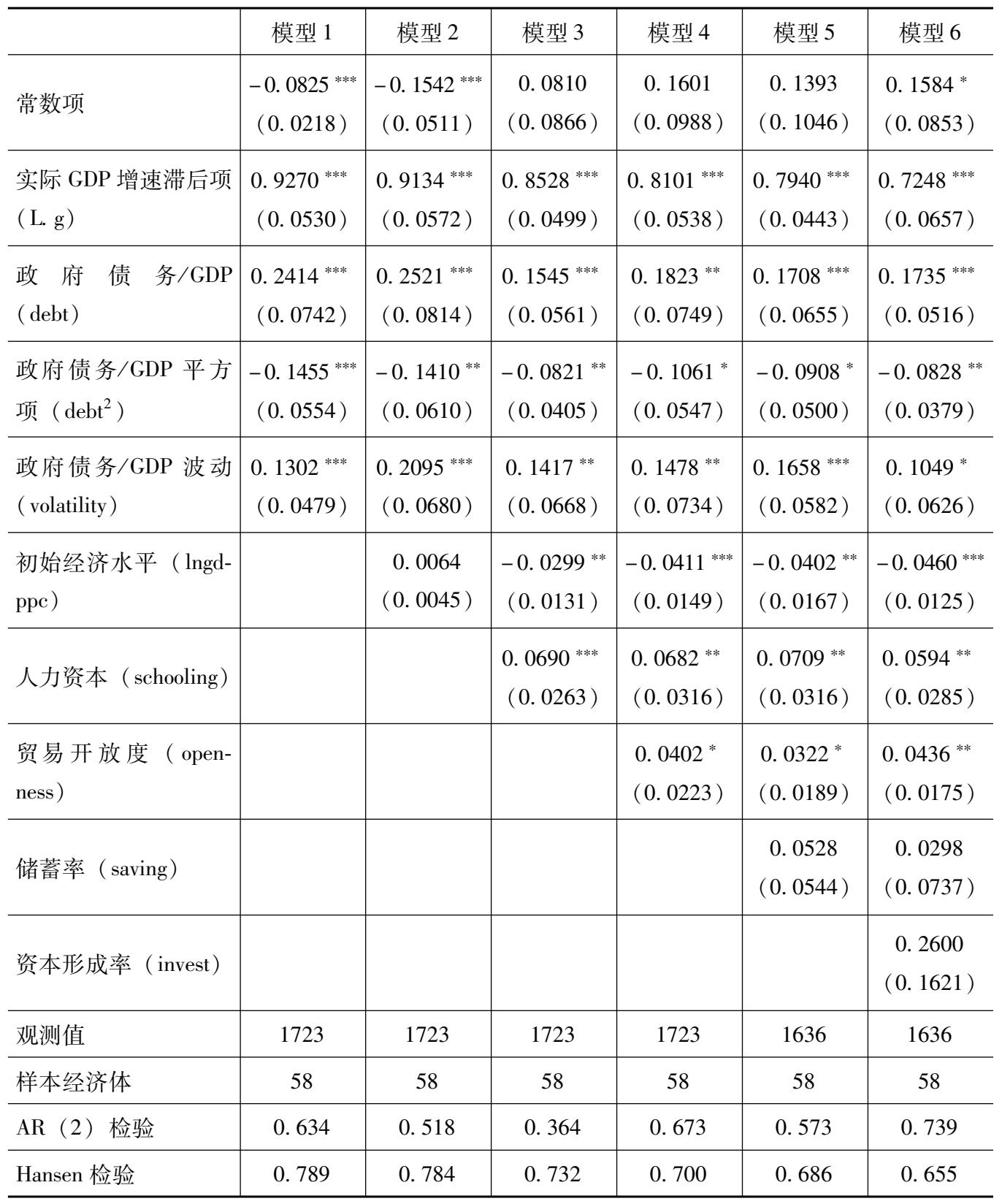
注:(1)*、**和***分别表示系数在10%、5%和1%的置信水平下显著;(2)括号内的值为对应变量回归系数的稳健标准误;(3)AR(2)检验和Hansen检验处为P值,AR(2)检验原假设为不存在二阶序列相关,Hansen检验原假设为工具变量有效。
2.基于人均实际GDP增长率的回归结果
在经典文献中,使用人均GDP指标可以更多从福利角度考察经济发展情况,多数文献都是同时研究整体GDP增速与人均GDP增速两种情形,我们也采用这样的方法。我们在这里将被解释变量选为人均实际GDP增速,同样使用系统GMM估计方法对政府债务与经济增长之间的关系进行研究,并逐步加入控制变量。结果如表3.3所示。
在表3.3中,模型1至模型6均通过工具变量有效性和二阶自相关的检验,说明估计结果是有效的。以人均实际GDP增速作为被解释变量的回归结果与以实际GDP增速作为被解释变量的回归结果是一致的。
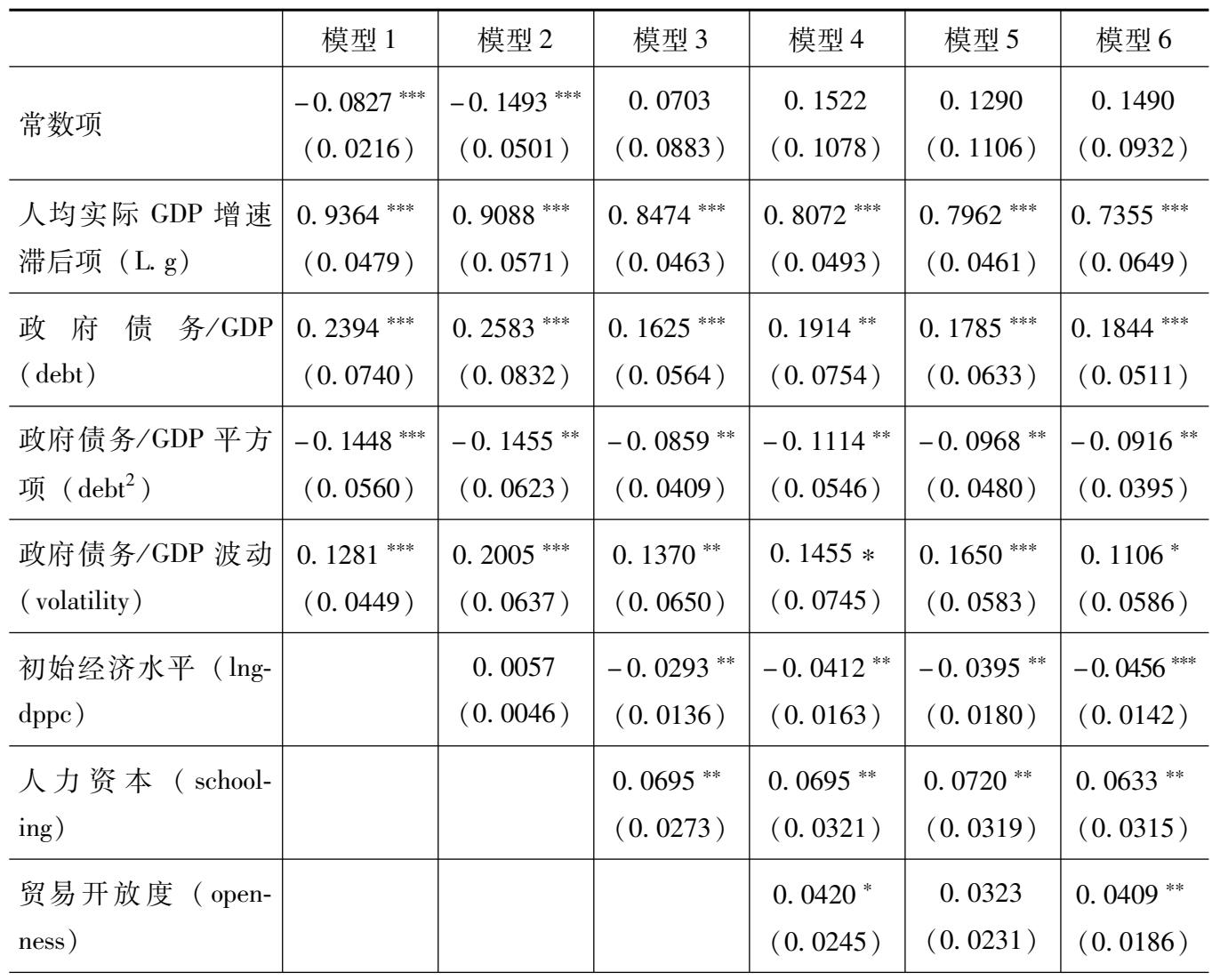
表3.3 政府债务对经济增长影响回归结果(1980—2015年)(人均实际GDP增速)
续表
注:(1)*、**和***分别表示系数在10%、5%和1%的置信水平下显著;(2)括号内的值为对应变量回归系数的稳健标准误;(3)AR(2)检验和Hansen检验处为P值,AR(2)检验原假设为不存在二阶序列相关,Hansen检验原假设为工具变量有效。
第一,核心解释变量政府债务(debt)、政府债务的二次项(debt 2 )以及政府债务波动(volatility)至少在10%置信水平下显著,并且符号依次为正、负、正,也证实政府债务水平与经济增长之间存在显著的非线性关系,同时政府债务波动对经济有一定的稳定作用。此外,以人均实际GDP增速作为被解释变量和实际GDP增速作为被解释变量的回归结果中,模型1至模型6每个解释变量在回归系数数值上的差异不大,表明估计结果是稳健的。
第二,以人均实际GDP增速作为被解释变量,通过模型1至模型6回归结果算出政府债务与经济增长关系变化的阈值分别为82.7%、88.8%、94.6%、85.9%、92.2%、100.7%,也在80%~105%的区间内,与以实际GDP增速作为被解释变量的回归结果计算出的阈值基本一致,进一步表明了模型的稳健性。
3.稳健性检验
为进一步考察估计结果的稳健性,我们选取1980年至2007年的数据进行分析,目的是排除2008年国际金融危机的影响。这主要是考虑到2008年国际金融危机影响较大,经济增速明显下降同时政府债务快速上升,可能会影响回归结果的准确性。
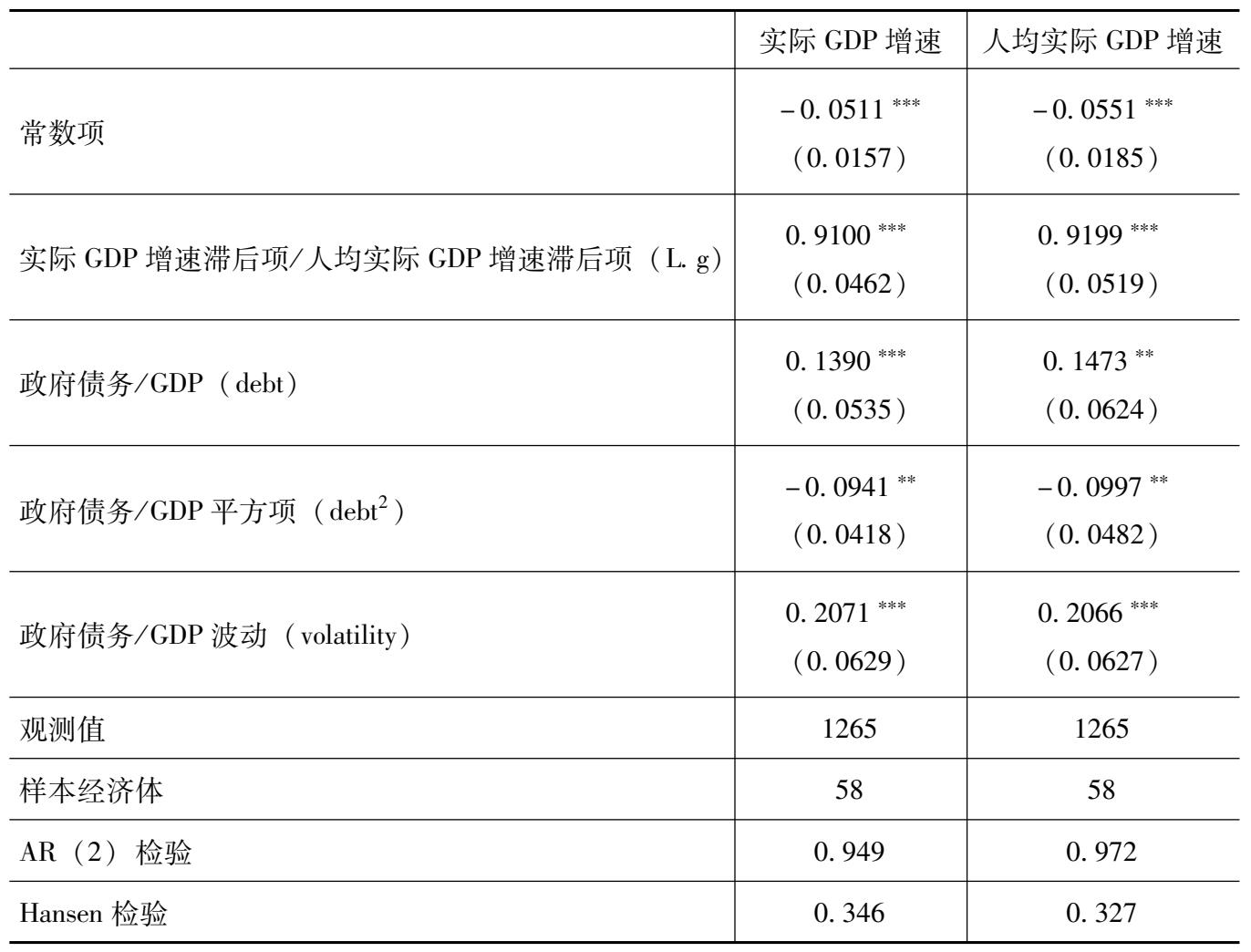
相关回归结果见表3.4,可以看出不论是选择以实际GDP增速还是人均实际GDP增速作为解释变量,政府债务(debt)、政府债务的二次项(debt 2 )以及政府债务波动(volatility)的符号与1980年至2015年数据回归结果是一致的,并且至少在5%的置信水平下显著。这同样表明政府债务对经济增长的影响是非线性的,并且政府债务波动对经济增长有促进作用。
表3.4 政府债务对经济增长影响回归结果(1980—2007年)
注:(1)*、**和***分别表示系数在10%、5%和1%的置信水平下显著;(2)括号内的值为对应变量回归系数的稳健标准误;(3)AR(2)检验和Hansen检验处为P值,AR(2)检验原假设为不存在二阶序列相关,Hansen检验原假设为工具变量有效。
选用1980年至2007年数据后,政府债务与经济增长关系变化的阈值有所下降。以实际GDP增速为被解释变量,阈值为73.9%;以人均实际GDP增速为被解释变量,阈值也为73.9%,略小于使用1980年至2015年数据计算出的阈值(使用实际GDP增速时为83.0%,使用人均实际GDP增速时为82.7%)。可能的原因是,在2008年国际金融危机的冲击下,各国为应对金融危机普遍实施了大规模的扩张性财政政策,政府债务上升较快,因此导致阈值水平上升。例如,美国政府债务/GDP 2016年为40%,而在2007年时则不到10%。
中国政府债务占GDP的比重问题值得关注。如图3.5所示,按照国际清算银行(BIS)统计口径,2017年中国政府债务/GDP为46.2%。中国政府债务/GDP自1997年以来呈逐年上升态势,与印度、美国和德国等相比,中国政府债务/GDP仍处于相对较低水平。印度政府债务/GDP比较稳定,接近70%;2008年国际金融危机以来,美国政府债务/GDP快速上升,2012年后稳定在96%左右;德国政府债务水平近几年有所下降,但仍在欧盟警戒线(60%)以上。虽然中国政府债务/GDP低于欧盟警戒线、我们和Rogoff和Reinhart(2010a)等估算的阈值(90%左右),但值得注意的是,上述政府债务统计未包含地方政府融资平台债务等隐性债务,考虑到隐性债务后实际债务水平会有比较明显的上升。
分析政府债务对经济增长的影响时,应考虑隐性债务。按照BIS的统计口径,虽然从法律关系上来看,地方政府融资平台债务属于企业债务,但却隐含着地方政府的隐性担保,其中部分最终可能需由地方政府承担。哈维·罗森(1992)开始关注政府隐性债务问题,他认为政府隐性债务是由政府承诺未来支付一定数额款项而产生的,广义政府债务应包括由担保承诺而形成的隐性债务。同时,应根据研究目的界定政府债务范围:若研究债务转移及债务最终归宿问题,就应将隐性债务包括在政府广义债务中;若研究政府债务对金融市场的影响,那么就不应该将隐性债务包含在内。我国地方融资平台资金多投向基础设施建设等领域。前文已经提到,政府债务在长期可能通过高通胀、高利率以及高税收预期等方式影响资本形成,最终影响经济增长。
我国广义政府债务/GDP可能已接近阈值[(80%~105%)以及Rogoff和Reihant(2010)等估算的阈值(90%)],我们测算的政府债务阈值在80%~105%之间,由此看政府债务仍有一定增长空间,但增长的空间已经不大,加强债务管理是必要的。
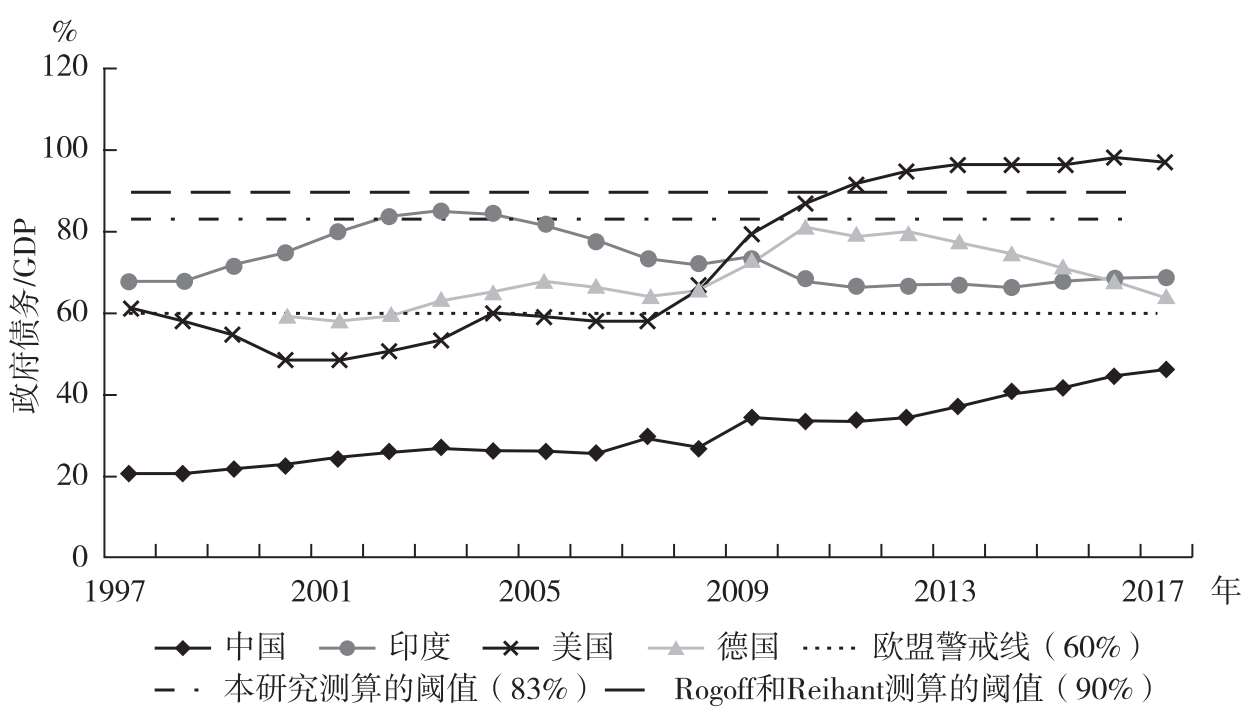
图3.5 1997—2017年各国政府债务占比情况
(数据来源:BIS数据库)

疫情起落,杠杆升降。新冠纾困之下各国债台高筑,我国宏观杠杆率也明显提升。以2020年为例,我国企业(含融资平台)杠杆率大幅上升12.7个百分点,政府和居民分别上升6.4个和5.6个百分点。但权宜之计并非长久之策。随着疫情退潮及出口高位,举债退潮乃情理之中。
值得一提的是,外需冷暖与国内杠杆率增速之间往往存在负向关系。例如,2002—2005年杠杆率增速下降就与外需相关。如果美国在加杠杆,或我国出口较好时,并不需要国内大量刺激。当然,2016年有些特殊,原因是国内主动开启了去杠杆进程。
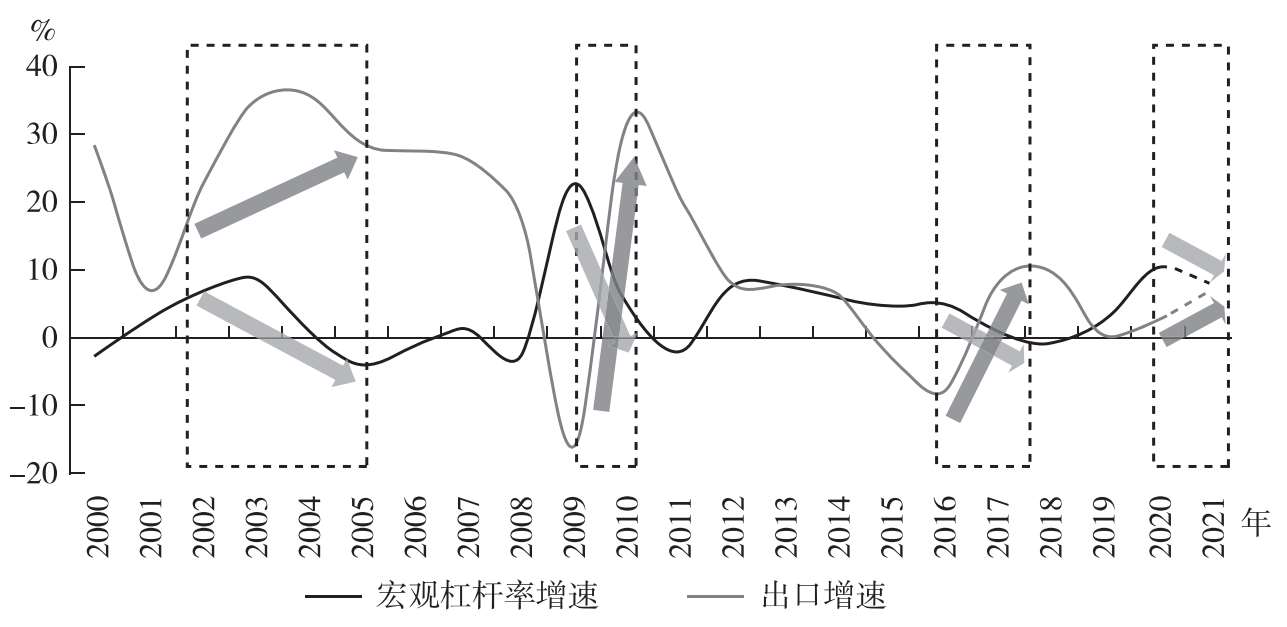
图3.6 外需“加杠杆”,内需“减杠杆”
(数据来源:Wind,笔者整理)
从地域结构来看,近年来我国经济、财政等发展呈现明显不平衡,中西部累积的信用风险远高于东部。新冠疫情期间,东部受到出口向好的影响,其财政收入增速抬升,而中西部仍处下行态势。疫情或将加重未来债务杠杆及其信用风险的区域不平衡。
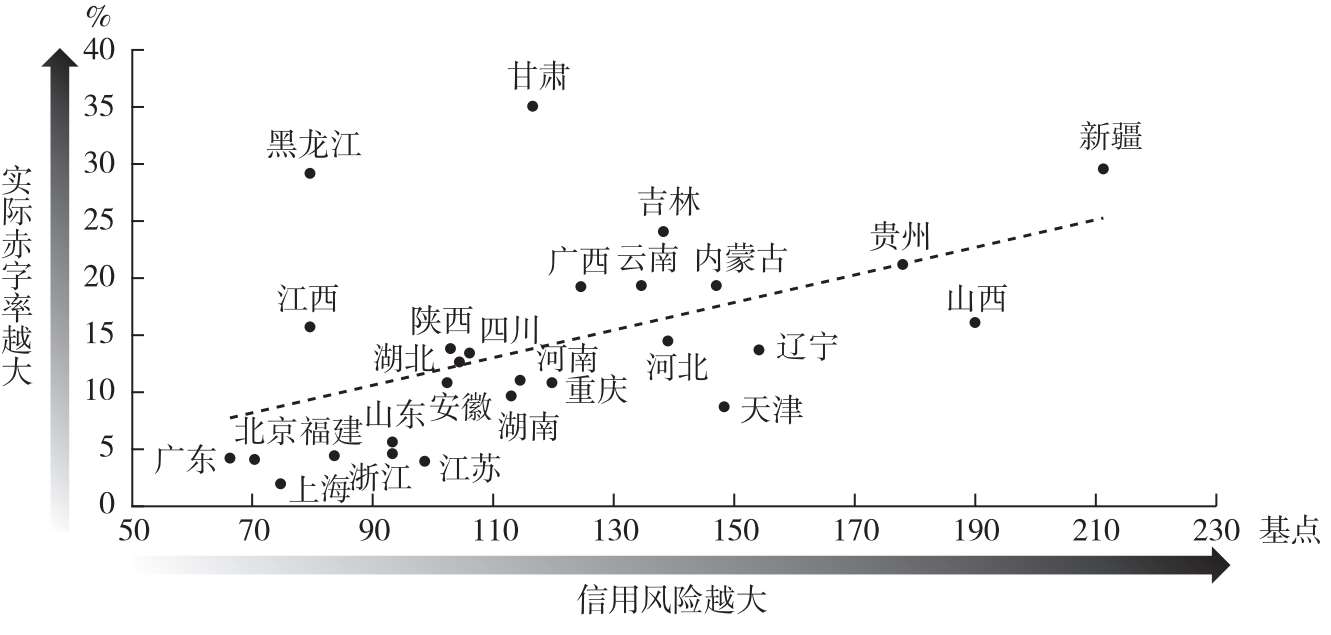
注:信用风险以各省份产业债利差表征。
图3.7 债务风险地域差异明显
(数据来源:Wind,笔者整理)
本章较为系统地回顾了有关政府债务与经济增长关系的文献,并在一个统一的框架下分析了政府债务短期和长期对经济增长的不同影响机制。理论研究表明,政府债务扩张短期能够刺激总需求进而促进经济增长,但债务持续积累长期则会影响资本形成、人力资本和技术水平等,进而抑制经济增长。从理论上看,政府债务扩张和经济增长之间存在“倒U形”关系。
在此基础上,我们基于58个国家和地区1980年至2015年的动态面板数据,采用系统GMM估计方法对政府债务、政府债务波动和经济增长关系进行了实证研究。结果表明,政府债务与经济增长之间确实存在较为显著的“倒U形”关系,随着政府债务的增加,对经济增长的作用会由促进转为抑制,并且存在相关关系变化的拐点和阈值,依据1980年至2015年数据计算出阈值在80%~105%之间,与Rogoff和Reinhart(2010)、Kumar和Woo(2010)计算的90%左右的阈值大体一致。此外,政府债务波动对稳定经济增长有一定的正向作用,表明财政政策可以起到逆周期调节、促进经济增长的作用。
若不考虑地方融资平台等隐性债务,我国目前政府债务/GDP在50%左右,低于欧盟警戒线(60%)、我们测算的阈值(80%~105%)及Rogoff和Reinhart等学者测算的阈值(90%)。若将地方融资平台债务纳入广义政府债务中,根据学者及相关机构的测算,广义政府债务/GDP可能超过80%,接近90%的阈值水平。我们的研究发现,所谓“内债不是债”,政府债务可持续扩张的观点并不准确,过度债务积累会对经济增长产生长期和深远的影响。我国政府债务扩张仍有一定空间,但已比较有限,要加强政府债务管理,尽量稳住宏观杠杆率。这既有利于保持经济长期发展,维护长期发展战略机遇期,也可为短期内财政货币政策逆周期调节赢得空间,促进和维护经济平稳增长。
[1] Elmendorf和Mankiw(1999)建立的分析框架:(1)私人部门预算约束为:私人部门的总收入=消费+储蓄+税收,即 Y = C + S + T ;(2)国民收入等于产出:总产出=消费+投资+政府支出+净出口,即 Y = C + I + G + NX ;(3)综合(1)和(2)得出, S+ ( T-G ) =I+NX ;(4)国家经常账户盈余和资本账户赤字:即 NX = NFI ;(5)综合(3)和(4)得出,私人部门的储蓄+政府部门的储蓄=本地投资+国外投资,即 S+ ( T-G ) =I+NFI 。