




此方圆之法 [2] 。此言求圆于方之法。 万物周事而圆方用焉,大匠造制而规矩设焉。或毁方而为圆,或破圆而为方 [3] 。圆中为方者谓之方圆,方中为圆者谓之圆方也 [4] 。
[1] 勾股圆方图:古代数学家商高、赵爽证明勾股定理所使用的图形。底本原图已佚,今补正如图14。图中标题“方圆图”“圆方图”是根据原文“圆中为方者谓之方圆,方中为圆者谓之圆方也”所加。
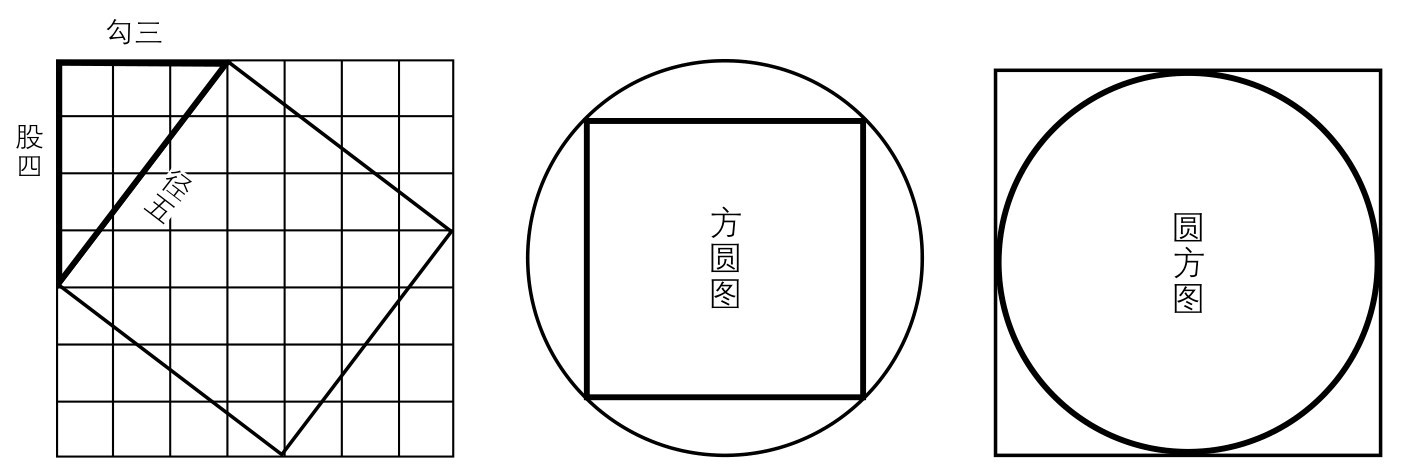
(图14)
[2] 此方圆之法:这是通过方形得到圆形的方法。正如赵爽所注“此言求圆于方之法”。
[3] 或毁方而为圆,或破圆而为方:(由方形得圆形)需打破正方形变为多边形,以此不断地趋近圆形,或切割圆弧为多段作为多边形的近似边。
[4] 圆中为方者谓之方圆,方中为圆者谓之圆方也:方圆图是由内接正方形向外推算圆的示意图;圆方图是由外切正方形向内推算圆的示意图。
这是方圆之法。 这是通过方形求得圆形的方法。 周围的万事万物都要用到圆形和方形,大工匠为制作物品而设计了规和矩。由方形求得圆形,或需打破正方形变为多边形,以此不断地趋近圆形,或切割圆弧为多段作为多边形的近似边。由内接正方形向外推算圆的示意图称为方圆图,由外切正方形向内推算圆的示意图称为圆方图。