3.3 求解关系模式的候选键

候选键的求解在关系规范化理论中至关重要，只有正确求得了候选键，才能进一步判断一个关系模式中的数据依赖的类型，以及关系模式的范式级别。

3.3.1 候选键的求解方法

关系模式的候选键是指能够唯一标识关系的元组的一个属性或属性组，可以根据候选键的定义从属性之间的联系判断候选键，也可以根据函数依赖的定义判断关系模式的候选键。如果关系模式中所有的属性都函数依赖于某个属性或属性组，则该属性或属性组即为关系模式R的候选键。

1. 逻辑蕴涵

只根据关系模式的函数依赖集中的函数依赖判断候选键是不够的，任何能够从函数依赖集推导出的其他函数依赖也是判断候选键的依据。

设关系模式R(U, F)中的U为属性集，F为函数依赖集，任何一个F中的函数依赖或者能够从F中推导出来的函数依赖X→Y，都被称为F逻辑蕴涵X→Y，或X→Y被F逻辑蕴涵。

例3-5 设关系模式student (SID, sname, gender, college, MID)的函数依赖集F={SID→sname, SID→gender, SID→college, college→MID}，函数依赖SID→MID是否被F逻辑蕴涵？

由SID→college, college→MID可以推出SID→MID在student上也成立，则除了SID→sname, SID→gender, SID→college, college→MID被F逻辑蕴涵外，SID→MID也被F逻辑蕴涵，或称F逻辑蕴涵SID→MID。

2. 函数依赖集F的闭包

F逻辑蕴涵的所有函数依赖的集合被称为F的闭包，记为F ⁺ 。

例如，关系模式student（SID, sname, gender, college, MID）中，函数依赖集合F的闭包F ⁺ ={SID→sname, SID→gender, SID→college, college→MID, SID→MID}。

3. 属性或属性集的闭包

基于函数依赖集F的闭包，可以求解任何一个属性或属性集能够函数决定的所有属性。属性或属性集能函数决定的所有属性，称为该属性或属性集的闭包，记为 。

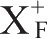设关系模式R中，U为属性集，F为函数依赖集，如果一个属性或属性集X能函数决定关系模式的所有属性，即 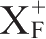=U，则X为关系模式的一个超键。如果 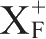=U且X的任何真子集关于F的闭包都不为U，则X是关系模式R的一个候选键。

综上，在求解复杂关系模式的候选键时，我们先要求解逻辑蕴涵，再求解函数依赖集的闭包和属性集的闭包。

3.3.2 Armstrong公理

1974年，Armstrong总结了各种函数推理规则，并把其中最主要、最基本的规则整理成了著名的Armstrong公理。Armstrong公理已被证明是一套有效的、完备逻辑蕴涵求解推理规则。

设关系模式R中，U为属性集，F为函数依赖集，则有如下推理规则。

（1）自反律。若属性集Y包含于属性集X，属性集X包含于U，则X→Y在R上成立。

（2）增广律。若X→Y在R上成立，且属性集Z包含于属性集U，则XZ→YZ在R上成立。

（3）传递律。若X→Y和Y→Z在R上成立，则X→Z在R上成立。

（4）合并规则。若X→Y，X→Z同时在R上成立，则X→YZ在R上也成立。

（5）分解规则。若X→W在R上成立，且属性集Z包含于W，则X→Z在R上也成立。

（6）伪传递规则。若X→Y在R上成立，且WY→Z，则XW→Z也成立。

例3-6 设关系模式R中，U={A, B, C, D, E, P}，F={AD→E, AE→BC, BE→DP, CD→E, CEP→D, DE→P, E→C, P→AB}，判断DP→CE是否属于F ⁺ 。

由P→AB知P→A，DP→AD。

又知AD→E，E→C，由传递律可得AD→C，由合并规则可得AD→CE。

由传递律可得DP→CE，所以DP→CE属于F ⁺ 。

通过上述步骤找到了F的一个逻辑蕴涵DP→CE。反复使用Armstrong公理，可以找出F逻辑蕴涵的所有函数依赖，进而得到F ⁺ 。但是对于属性多的关系模式，这种方法的求解过程会比较烦琐。

3.3.3 求解属性集的闭包

由 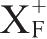的定义可知，若想判断函数依赖X→Y是否成立，只要计算X关于函数依赖集F的闭包，若X的闭包中包含Y，则X→Y成立。计算 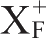的过程如下。

（1）选X为初值记为X ⁽ⁱ⁾ ，i=0。

（2）求A，这里A满足下列条件：Y⊆X ⁽ⁱ⁾ 且F中存在函数依赖Y→Z，而A⊆Z，X ⁽ⁱ⁺¹⁾ =A∪X ⁽ⁱ⁾ 。

（3）判断X ⁽ⁱ⁺¹⁾ 是否等于X ⁽ⁱ⁾ 。若相等或X ⁽ⁱ⁾ =U，则X ⁽ⁱ⁾ 就是 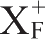，算法终止。否则i=i+l，返回第（2）步。

例3-7 设关系模式R中，U={A, B, C, D, E, P}，F={AE→BC, AP→E, CD→E, CE→D, DE→P, E→C, P→A}，判断DP是否为关系模式的候选键。

设X ⁽⁰⁾ =DP。

计算X ⁽¹⁾ ：在F中找其左边为D或P或DP的函数依赖，如P→A，所以X ⁽¹⁾ =DP∪A=ADP。

计算X ⁽²⁾ ：在F中找包含X ⁽¹⁾ 的函数依赖，除P→A外，还有AP→E，所以X ⁽²⁾ =ADP∪E=ADEP。

计算X ⁽³⁾ ：在F中找包含X ⁽²⁾ 的函数依赖，除去已使用过的函数依赖外，还有E→C，DE→P和AE→BC，所以X ⁽³⁾ =ADEP∪BC=ABCDEP。

由上述计算可得(DP) ⁺ =ABCDEP，DP是超键，而且它的任何一个真子集D或P都不能函数决定关系模式的全部属性，因此DP是关系R的候选键。

3.3.4 简化候选键的求解过程

通过求 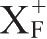求候选键时的最大问题就是对所有属性都要计算，特别不适合多属性的情况。如果能事先把根本不可能是主属性的属性去掉，将会大大缩短求解过程。

对于关系模式R中的任何一个函数依赖X→Y，左边的属性X是决定性属性，右边的属性Y是依赖性属性。如果关系模式的某个属性只出现在函数依赖的左边，这个属性不仅是决定性属性，而且不能由其他决定性属性推导出来，一定是任一候选键的组成部分，被称为L类属性。对于那些只出现在函数依赖右边的属性，则一定不是主属性，不存在于关系模式的任何候选键中，称为R类属性。在函数依赖的左右两边都出现过的属性，称为LR类属性。没有办法直接判断LR类属性是否包含在候选键中，需要通过属性的闭包进行分析。最后一类是在函数依赖左右两边均未出现的孤立属性，被称为N类属性。N类属性虽然不能决定其他属性，但是也不能由其他属性推导出来，即N类属性不可能包含在其他属性的闭包中，因此N类属性和L类属性一样，是任一候选键的组成部分。

根据以上属性的分类方法，可以排除求解R类属性的闭包，简化候选键的求解过程。

例3-8 设关系模式R(U, F)，U={A, B, C, D, E}，F={AB→CD, E→D, D→E, AE→BC, B→E}，求所有候选键。

A不在函数依赖集F中任何一个函数依赖的右边出现，R的候选键必含A；

A ⁺ =A，所以A不是候选键。

(AB) ⁽⁰⁾ =AB，AB→CD，B→E，所以(AB) ⁽¹⁾ =ABCDE。(AB) ⁺ =ABCDE=U，所以AB是候选键。

(AC) ⁽⁰⁾ =AC，(AC) ⁺ =AC，所以AC不是候选键。

(AD) ⁽⁰⁾ =AD，D→E，所以(AD) ⁽¹⁾ =ADE。E→D，AE→BC，所以(AD) ⁽²⁾ =ADEBC。(AD) ⁺ =ADEBC=U，所以AD是候选键。

(AE) ⁽⁰⁾ =AE，AE→BC，E→D，所以(AE) ⁽¹⁾ =AEBCD。(AE) ⁺ =AEBCD=U，所以AE是候选键。

有3个及3个以上属性且含A的子集都含AB或AD或AE，都是超键，不是候选键。

所以R的候选键有AB，AD，AE。 Dtxxdoi740AIAscTdmG8OZ8mtdCRxm4PwYGH7zEFMeqVzSwpMTo265fboG2xzKz9