




APTC eliminates the differences of structures of transition systems,event structures,etc.,and discusses their behavioral equivalences.It considers two kinds of causality relations:the chronological order modeled by sequential composition and the causal order between different parallel branches modeled by communication merge.It also considers two kinds of confliction relations:the structural confliction modeled by alternative composition and the conflicts in different parallel branches that should be eliminated.Based on conservative extension,APTC has four modules:BATC(Basic Algebra for True Concurrency),APTC(Algebra for Parallelism in True Concurrency),recursion and abstraction.
BATC has sequential composition·and alternative composition+to capture the chronological ordered causality and the structural confliction.The constants are ranged over A ,the set ofatomic actions.The algebraic laws on·and+are sound and complete modulo truly concurrent bisimulation equivalences(including pomset bisimulation,step bisimulation,hp-bisimulation and hhp-bisimulation).
Definition 2.15
(Prime event structure with silent event).Let
Λ
be afixed set of labels,ranged over
a,b,c,···
and
τ
.A(
Λ
-labelled)prime event structure with silent event
τ
is a tuple
E
=〈E,≤,
♯,λ
〉,where E is a denumerable set of events,including the silent event
τ
.Let
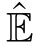 =E \{τ},exactly excluding
τ
,it is obvious that
=E \{τ},exactly excluding
τ
,it is obvious that
 =
∊
,where
∊
is the empty event.Let
λ
:E
=
∊
,where
∊
is the empty event.Let
λ
:E
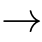 Λ
be a labelling function,and let
λ
(
τ
)=
τ
.And≤,
♯
are binary relations on E,called causality and conflict respectively,such that:
Λ
be a labelling function,and let
λ
(
τ
)=
τ
.And≤,
♯
are binary relations on E,called causality and conflict respectively,such that:
(1)≤is a partial order,and 「e
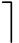 ={
e'
∈E|
e'
≤
e
}is finite for all
e
∈E.It is easy to see that if
e
≤
τ
⋆
≤
e'
=
e
≤
τ
≤ ···≤
τ
≤
e'
,then
e
≤
e'
;
={
e'
∈E|
e'
≤
e
}is finite for all
e
∈E.It is easy to see that if
e
≤
τ
⋆
≤
e'
=
e
≤
τ
≤ ···≤
τ
≤
e'
,then
e
≤
e'
;
(2) ♯ is irreflexive,symmetric,and hereditary with respect to≤.That is,for all e,e',e '' ∈E,if e♯e' ≤ e '' ,then e♯e '' .
Then,the concepts of consistency and concurrency can be drawn from the above definition:
(1) e,e' ∈E are consistent,denoted e⌒e' ,if ¬( e♯e' ).A subset X⊆ E is called consistent,if e⌒e' for all e,e' ∈ X ;
(2) e,e' ∈E are concurrent,denoted e‖e' ,if ¬( e ≤ e' ), ¬( e' ≤ e ),and ¬( e♯e' ).
Definition 2.16
(Configuration).Let
E
be a PES.A(finite)configuration in
E
is a(finite)consistent subset of events
C⊆E
,closed with respect to causality(i.e. 「C
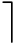 =
C
).The set of finite configurations of
E
is denoted by
C
(
E
).We let
=
C
).The set of finite configurations of
E
is denoted by
C
(
E
).We let
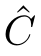 =C\{τ}.
=C\{τ}.
A consistent subset of
X⊆
E of events can be seen as apomset.Given
X,Y⊆
E,
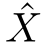 ~
~
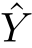 if
if
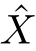 and
and
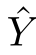 are isomorphic as pomsets.In the following of the paper,when we say
C
1
~C
2
,we mean
are isomorphic as pomsets.In the following of the paper,when we say
C
1
~C
2
,we mean
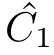 ~
~
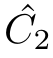 .
.
Definition 2.17
(Pomset transitions and step).Let
E
be a PES,
C
∈
C
(
E
),and∅ /=
X⊆
E,if
C∩X
=∅and
C'
=C∪X∈
C
(
E
),then
C
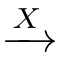 C'
is called a pomset transition from
C
to
C'
.When the events in
X
are pairwise concurrent,we say that
C
C'
is called a pomset transition from
C
to
C'
.When the events in
X
are pairwise concurrent,we say that
C
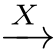 C'
is a step.
C'
is a step.
Definition 2.18
(Pomset and step bisimulation).Let
E
1
and
E
2
be PESs.A pomset bisimulation is a relation
R⊆C
(
E
1
)
×C
(
E
2
),such that if(
C
1
,
C
2
)∈
R
,and
C
1
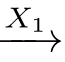 C
1
'
,then
C
1
'
,then
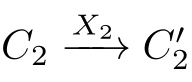 , with
X
1
⊆
E
1
,
X
2
⊆
E
2
,
X
1
~X
2
,and(
, with
X
1
⊆
E
1
,
X
2
⊆
E
2
,
X
1
~X
2
,and(
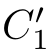 ,
,
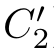 )∈
R
,and vice-versa.We say that
E
1
and
E
2
are pomset bisimilar,written
E
1
~
p
E
2
,if there exists a pomset bisimulation
R
,such that(∅,∅)∈
R
.By replacing pomset transitions with steps,we can get the def inition of step bisimulation.When PESs
E
1
and
E
2
are step bisimilar,we w rite
E
1
~
s
E
2
.
)∈
R
,and vice-versa.We say that
E
1
and
E
2
are pomset bisimilar,written
E
1
~
p
E
2
,if there exists a pomset bisimulation
R
,such that(∅,∅)∈
R
.By replacing pomset transitions with steps,we can get the def inition of step bisimulation.When PESs
E
1
and
E
2
are step bisimilar,we w rite
E
1
~
s
E
2
.
Definition 2.19
(Posetal product).Given two PESs
E
1
and
E
2
,the posetal product of their conigurations,denoted
C
(
E
1
)
 C
(
E
2
),is defined as
C
(
E
2
),is defined as
{(
C
1
,
f,C
2
)|
C
1
∈
C
(
E
1
),
C
2
∈
C
(
E
2
),
f
:
C
1
 C
2
isomorphism}
C
2
isomorphism}
A subset
R⊆C
(
E
1
)
 C
(
E
2
)is called a posetal relation.We say that
R
is downward closed when for any(
C
1
,
f,C
2
),(
C
(
E
2
)is called a posetal relation.We say that
R
is downward closed when for any(
C
1
,
f,C
2
),(
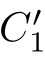 ,
f',
,
f',
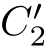 )∈
C
(
E
1
)
)∈
C
(
E
1
)
 C
(
E
2
),if(
C
1
,
f,C
2
)
⊆
(
C
(
E
2
),if(
C
1
,
f,C
2
)
⊆
(
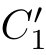 ,
f',
,
f',
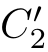 )point wise and(
)point wise and(
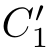 ,
f',
,
f',
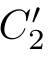 )∈
R
,then(
C
1
,
f,C
2
)∈
R
.
)∈
R
,then(
C
1
,
f,C
2
)∈
R
.
For
f
:
X
1
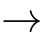 X
2
,we define
f
[
x
1
X
2
,we define
f
[
x
1
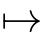 x
2
]:
X
1
∪{
x
1
}
x
2
]:
X
1
∪{
x
1
}
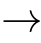 X
2
∪{
x
2
},
z
∈
X
1
∪{
x
1
}as follows:①
f
[
x
1
X
2
∪{
x
2
},
z
∈
X
1
∪{
x
1
}as follows:①
f
[
x
1
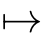 x
2
](
z
)=
x
2
,if
z
=
x
1
;②
f
[
x
1
x
2
](
z
)=
x
2
,if
z
=
x
1
;②
f
[
x
1
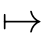 x
2
](
z
)=
f
(
z
),otherw ise.Here,
X
1
⊆
E
1
,
X
2
⊆
E
2
,
x
1
∈E
1
,and
x
2
∈E
2
.
x
2
](
z
)=
f
(
z
),otherw ise.Here,
X
1
⊆
E
1
,
X
2
⊆
E
2
,
x
1
∈E
1
,and
x
2
∈E
2
.
Definition 2.20
((Hereditary)history-preserving bisimulation).A history-preserving(hp-)bisimulation is a posetal relation
R⊆C
(
E
1
)
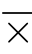 C
(
E
2
)such that if(
C
1
,
f,C
2
)∈
R
,and
C
(
E
2
)such that if(
C
1
,
f,C
2
)∈
R
,and
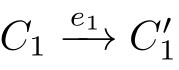 ,then
,then
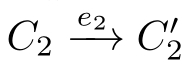 , with(
, with(
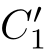 ,
f
[
e
1
,
f
[
e
1
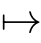 e
2
],
e
2
],
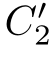 )∈
R
,and vice-versa.
E
1
and
E
2
are history-preserving(hp-)bisimilar and arewritten as
E
1
~
hp
E
2
if there exists a hp-bisimulation
R
such that(∅,∅,∅)∈
R
.
)∈
R
,and vice-versa.
E
1
and
E
2
are history-preserving(hp-)bisimilar and arewritten as
E
1
~
hp
E
2
if there exists a hp-bisimulation
R
such that(∅,∅,∅)∈
R
.
A hereditary history-preserving(hhp-)bisimulation is a downward closed hpbisimulation. E 1 and E 2 are hereditary history-preserving(hhp-)bisimulation and are written as E 1 ~ hhp E 2 .
In the following,let
e
1
,
e
2
,
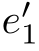 ,
,
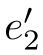 ∈E,and let variables
x,y,z
range over the set of terms for true concurrency,and variables
p,q,s
range over the set of closed terms.The set of axioms of BATC consists of the laws given in Table 2.1.
∈E,and let variables
x,y,z
range over the set of terms for true concurrency,and variables
p,q,s
range over the set of closed terms.The set of axioms of BATC consists of the laws given in Table 2.1.
Table 2.1 Axioms of BATC

Definition 2.21 (Basic terms of BATC).The set of basic terms of BATC,denoted B (BATC),is inductively defined as follows:
(1)E ⊂B (BATC).
(2)If e ∈E, t ∈ B (BATC),then e·t∈ B (BATC).
(3)If t,s∈ B (BATC),then t + s ∈ B (BATC).
Theorem 2.3 (Elimination theorem of BATC).Let p be a closed BATC term.Then there exists a basic BATC term q such that BATC ├ p = q .
We provide the operational transition rules of operators·and+as follows.The predicate
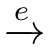 √
represents successful termination after execution of the event
e
.
√
represents successful termination after execution of the event
e
.
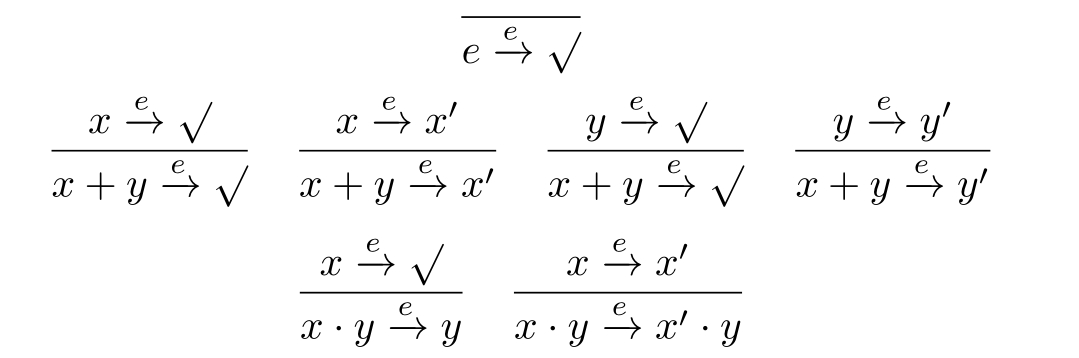
Theorem 2.4 (Congruence of BATC with respect to truly concurrent bisimulation equivalences).Truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp are all congruences with respect to BATC.
Theorem 2.5 (Soundness of BATC modulo truly concurrent bisimulation equivalences).The axiomatization of BATC is sound modulo truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp .That is,
(1)Let x and y be BATC terms,if BATC ├ x = y ,then x ~ p y .
(2)Let x and y be BATC terms,if BATC ├ x = y ,then x ~ s y .
(3)Let x and y be BATC terms,if BATC ├ x = y ,then x ~ hp y .
(4)Let x and y be BATC terms,if BATC ├ x = y ,then x ~ hhp y .
Theorem 2.6 (Completeness of BATC modulo truly concurrent bisimulation equivalences).The axiomatization of BATC is complete modulo truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp .That is,
(1)Let p and q be closed BATC terms,if p ~ p q ,then p = q .
(2)Let p and q be closed BATC terms,if p ~ s q ,then p = q .
(3)Let p and q be closed BATC terms,if p ~ hp q ,then p = q .
(4)Let p and q be closed BATC terms,if p ~ hhp q ,then p = q .
Since hhp-bisimilarities is a downward closed hp-bisimilarities and can be downward closed to a singleatomic event,which implies bisimilarities.As proven by M oller[9],there is no finite sound and complete axiomatization for parallelism‖modulo bisimulation equivalence,so there is no finite sound and comp lete axiomatization for parallelism‖modulo hhp-bisimulation equivalence either.Inspired by the approach of leftmerge used to model the fullmerge for bisimilarities,we introduce a left parallel composition
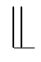 to model the full parallelism‖for hhp-bisimilarities.
to model the full parallelism‖for hhp-bisimilarities.
In the following subsection,we extend the theory by adding left parallel composition
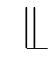 to the whole theory.Since the resulting theory is similar to the previous one,we will only highlight the significant differences,and the proofs of the conclusions are left to the reader.
to the whole theory.Since the resulting theory is similar to the previous one,we will only highlight the significant differences,and the proofs of the conclusions are left to the reader.
We provide the transition rules of APTC as follows,which are applicable to all truly concurrent behavioral equivalences,including pomset bisimulation,step bisimulation,hp-bisimulation and hhp-bisimulation.Where≬is the whole concurrency operator,‖is the parallel operator,
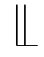 is the left parallel operator,|is the communication merge,
Θ
is the conflicts elimination operator,and
◁
is the auxiliary unless operator.
is the left parallel operator,|is the communication merge,
Θ
is the conflicts elimination operator,and
◁
is the auxiliary unless operator.

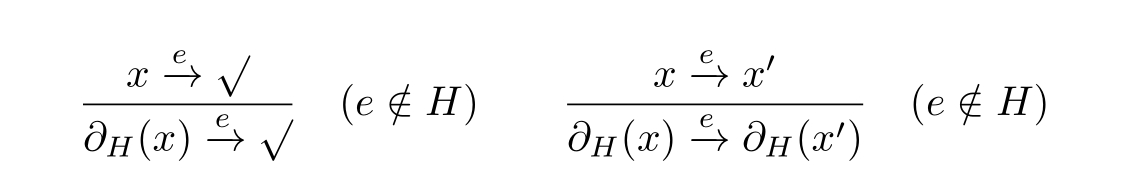
The transition rules of left parallel composition
 are presented as follows.With a little abuse,we extend the causal order relation≤on E to include the original partial order(denoted by <)and concurrency(denoted by=).
are presented as follows.With a little abuse,we extend the causal order relation≤on E to include the original partial order(denoted by <)and concurrency(denoted by=).
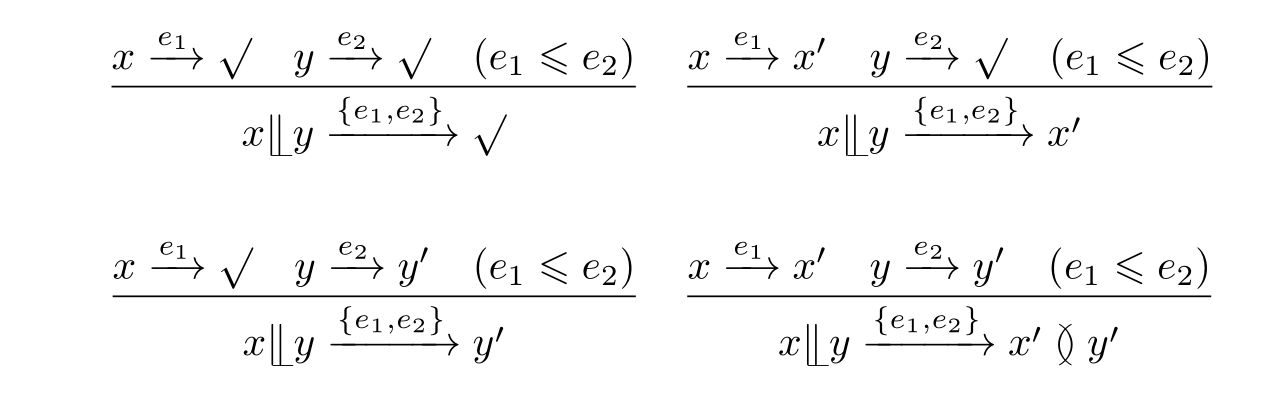
The new axioms for parallelism are listed in Table 2.2.
Definition 2.22 (Basic terms of APTC with left parallel composition).The set of basic terms of APTC,denoted B (APTC),is inductively defined as follows:
(1)E ⊂B (APTC).
(2)If e ∈E and t ∈ B (APTC),then e·t∈ B (APTC).
(3)If t,s∈ B (APTC),then t + s ∈ B (APTC).
(4)If t,s∈
B
(APTC),then
t
 s
∈
B
(APTC).
s
∈
B
(APTC).
Theorem 2.7 (Generalization of the algebra for left parallelism with respect to BATC).The algebra for left parallelism is a generalization of BATC.
Theorem 2.8 (Congruence theorem of APTC with left parallel composition).Truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp are all congruences with respect to APTC with left parallel composition.
Theorem 2.9 (Elimination theorem of parallelism with left parallel composition).Let p be a closed APTC with left parallel composition term.Then there is a basic APTC term q such that APTC ├ p = q .
Theorem 2.10 (Soundness of parallelism with left parallel composition modulo truly concurrent bisimulation equivalences).Let x and y be APTC with left parallel composition terms.If APTC ├ x = y ,then
(1) x ~ s y .
(2) x ~ p y .
(3) x ~ hp y .
(4) x ~ hhp y .
Table 2.2 Axioms of parallelism with left parallel composition
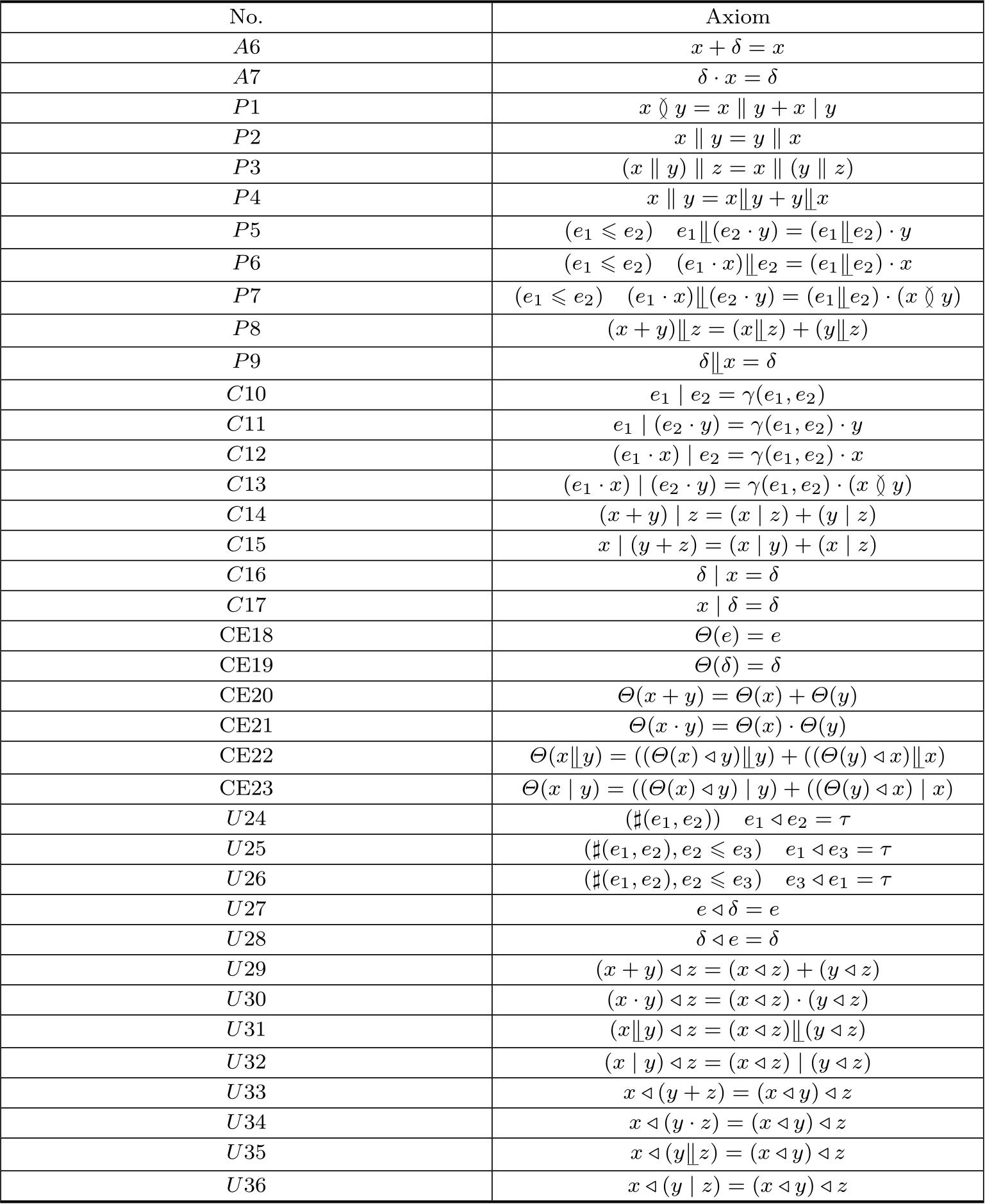
Theorem 2.11 (Completeness of parallelism with left parallel composition modulo truly concurrent bisimulation equivalences).Let x and y be APTC terms.
(1)If x ~ s y ,then APTC ├ x = y .
(2)If x ~ p y ,then APTC ├ x = y .
(3)If x ~ hp y ,then APTC ├ x = y .
(4)If x ~ hhp y ,then APTC ├ x = y .
The axioms of encapsulation operator are shown in Table 2.3.
Table 2.3 The axioms of encapsulation operator with left parallel composition

Theorem 2.12 (Conservativity of APTC with respect to the algebra for parallelism with left parallel composition).APTC is a conservative extension of the algebra for parallelism with left parallel composition.
Theorem 2.13 (Congruence theorem of encapsulation operator ∂ H ).Truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp are all congruences with respect to encapsulation operator ∂ H .
Theorem 2.14 (Elimination theorem of APTC).Let p be a closed APTC term including the encapsulation operator ∂ H .Then there exists a basic APTC term q such that APTC ├ p = q .
Theorem 2.15 (Soundness of APTC modulo truly concurrent bisimulation equivalences).Let x and y be APTC terms including encapsulation operator ∂ H .If APTC ├ x = y ,then
(1) x ~ s y .
(2) x ~ p y .
(3) x ~ hp y .
(4) x ~ hhp y .
Theorem 2.16 (Completeness of APTC modulo truly concurrent bisimulation equivalences).Let p and q be closed APTC terms including encapsulation operator ∂ H ,then
(1)If p ~ s q ,then p = q .
(2)If p ~ p q ,then p = q .
(3)If p ~ hp q ,then p = q .
(4)If p ~ hhp q ,then p = q .
Definition 2.23 (Recursive specification).A recursive specification is a finite set of recursive equations
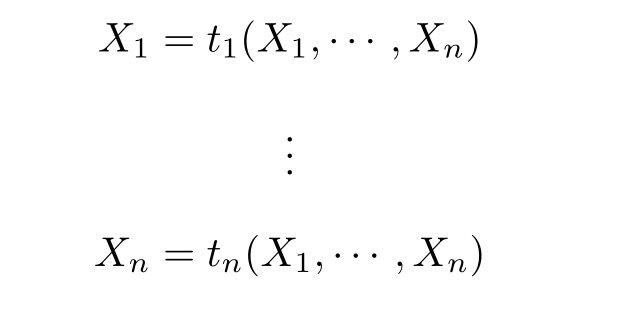
where the left-hand sides X i are called recursive variables,and the right-hand sides t i ( X 1 ,···, X n )are process terms in APTC with possible occurrences of the recursive variables X 1 ,···, X n .
Definition 2.24 (Solution).Processes p 1 ,···, p n are a solution for a recursive specification{ X i = t i ( X 1 ,···, X n )| i ∈{1,···, n }}(with respect to truly concurrent bisimulation equivalences~ s (~ p ,~ hp ,~ hhp ))if p i ~ s (~ p ,~ hp ,~ hhp ) t i ( p 1 ,···, p n )for i ∈{1,···, n }.
Definition 2.25 (Guarded recursive specification).A recursive specification
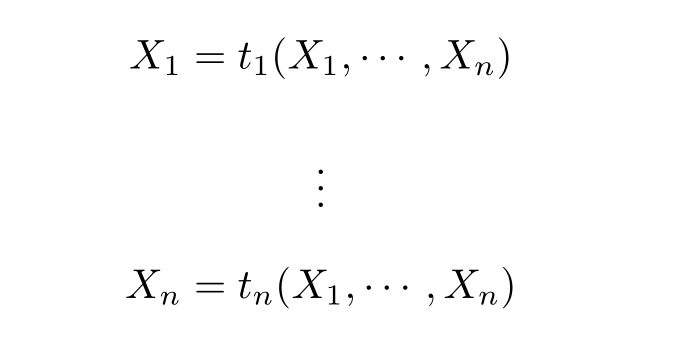
is guarded if the right-hand sides of its recursive equations can be adapted to the form by applications of the axioms in APTC,and replacing recursive variables by the right-hand sides of their recursive equations.
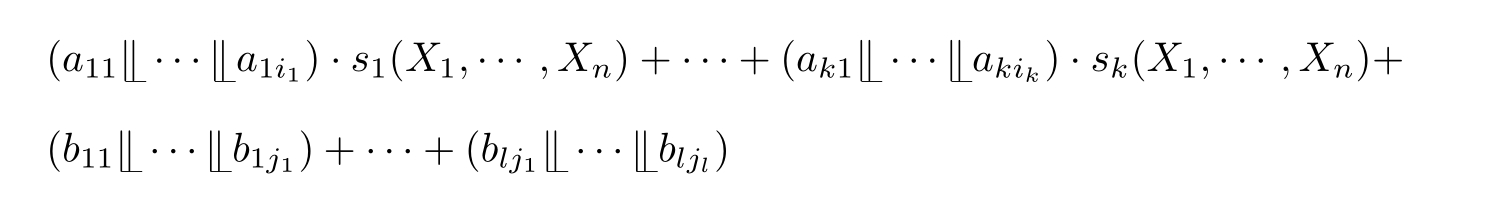
where
a
11
,···,
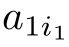 ,
a
k
1
,···,
,
a
k
1
,···,
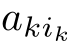 ,
b
11
,···,
,
b
11
,···,
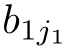 ,
,
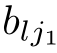 ,···,
,···,
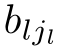 ∈E,and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
∈E,and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
Definition 2.26 (Linear recursive specification).A recursive specification is linear if its recursive equations are of the form:
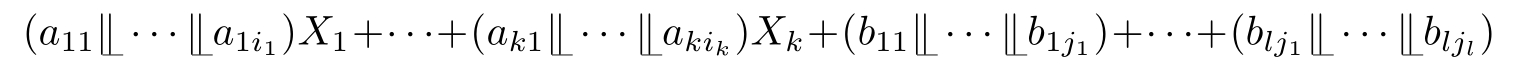
where
a
11
,···,
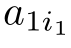 ,
a
k
1
,···,
,
a
k
1
,···,
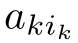 ,
b
11
,···,
,
b
11
,···,
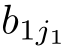 ,
,
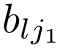 ,···,
,···,
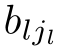 ∈E,and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
∈E,and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
The transition rules of recursive solution are following.
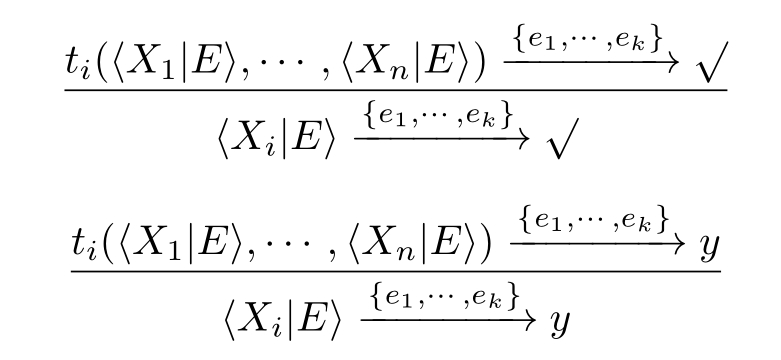
The RDP(Recursive Definition Princip le)and the RSP(Recursive Specification Principle)are shown in Table 2.4.
Table 2.4 Recursive definition and specification principle
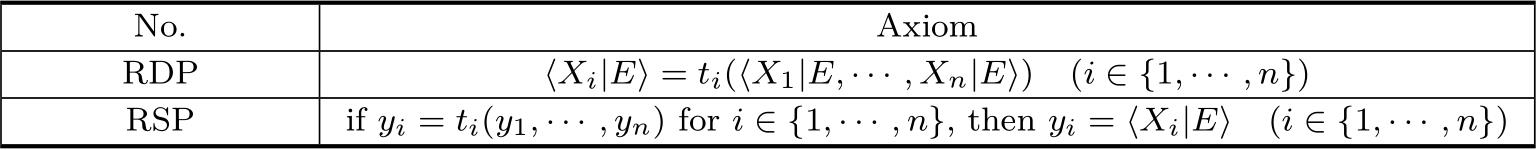
Theorem 2.17 (Conservativity of APTC with guarded recursion).APTC with guarded recursion is a conservative extension of APTC.
Theorem 2.18 (Congruence theorem of APTC with guarded recursion).Truly concurrent bisimulation equivalences~ p ,~ s ,~ hp ,and~ hhp are all congruences with respect to APTC with guarded recursion.
Theorem 2.19 (Elimination theorem of APTC with linear recursion).Each process term in APTC with linear recursion is equal to a process term〈 X 1 | E 〉 with E being a linear recursive specification.
The behavior of the solution〈 X i | E 〉for the recursive variable X i in E ,where i ∈{1,···, n },is exactly the behavior of their right-hand sides t i ( X 1 ,···, X n ),which is captured by the two transition rules of recursive solution.
Theorem 2.20 (Soundness of APTC with guarded recursion).Let x and y be APTC with guarded recursion terms.If APTC with guarded recursion ├ x = y ,then
(1) x ~ s y .
(2) x ~ p y .
(3) x ~ hp y .
(4) x ~ hhp y .
Theorem 2.21 (Completeness of APTC with linear recursion).Let p and q be closed APTC with linear recursion terms,then
(1)If p ~ s q ,then p = q .
(2)If p ~ p q ,then p = q .
(3)If p ~ hp q ,then p = q .
(4)If p ~ hhp q ,then p = q .
Definition 2.27
(Weak pomset transitions and weak steps).Let
E
be a PES,
C
∈
C
(
E
),and∅ /=
X⊆
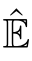 .If
C∩X
=∅and
.If
C∩X
=∅and
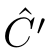 =
=
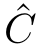 ∪
X
∈
C
(
E
),then
C
∪
X
∈
C
(
E
),then
C
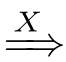 C'
is called a weak pomset transition from
C
to
C'
.Here,we define
C'
is called a weak pomset transition from
C
to
C'
.Here,we define
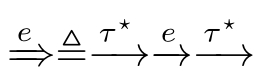 ,and
,and
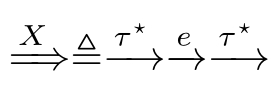 ,for every
e
∈
X
.When the events in
X
are pairwise concurrent,we say that
C
X
=⇒C'is a weak step.
,for every
e
∈
X
.When the events in
X
are pairwise concurrent,we say that
C
X
=⇒C'is a weak step.
Definition 2.28
(Branching pomset and step bisimulation).Assume a special termination predicate
 ,and let
√
represent a state with
√
,and let
√
represent a state with
√
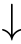 .Let
E
1
and
E
2
be PESs.A branching pomset bisimulation is a relation
R⊆C
(
E
1
)
×C
(
E
2
),such that:
.Let
E
1
and
E
2
be PESs.A branching pomset bisimulation is a relation
R⊆C
(
E
1
)
×C
(
E
2
),such that:
(1)If(
C
1
,
C
2
)∈
R
,and
 ,then
,then
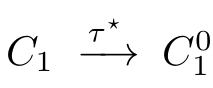
① X≡τ
⋆
,and(
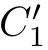 ,
C
2
)∈
R
;
,
C
2
)∈
R
;
②there is a sequence of(zero or more)
τ
-transitions
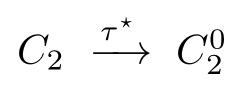 ,such that(
C
1
,
,such that(
C
1
,
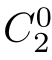 )∈
R
and
)∈
R
and
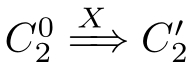 with(
with(
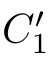 ,
,
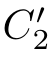 )∈
R
.
)∈
R
.
(2)If(
C
1
,
C
2
)∈
R
,and
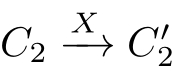 ,then
,then
① X≡τ
⋆
,and(
C
1
,
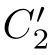 )∈
R
;
)∈
R
;
②There is a sequence of(zero or m ore)
τ
-transitions
 ,such that(
,such that(
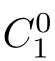 ,
C
2
)∈
R
and
,
C
2
)∈
R
and
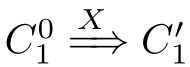 with(
with(
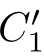 ,
,
 )∈
R
.
)∈
R
.
(3)If(
C
1
,
C
2
)∈
R
and
C
1
 ,then there is a sequence of(zero or more)
τ
transitions
,then there is a sequence of(zero or more)
τ
transitions
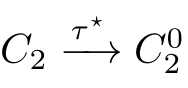 such that(
C
1
,
such that(
C
1
,
 )∈
R
and
)∈
R
and
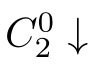 .
.
(4)If(
C
1
,
C
2
)∈
R
and
C
2
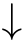 ,then there is a sequence of(zero or more)
τ
transitions
,then there is a sequence of(zero or more)
τ
transitions
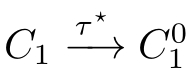 such that(
such that(
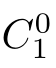 ,
C
2
)∈
R
and
,
C
2
)∈
R
and
 .
.
We say that E 1 and E 2 are branching pomset bisimilar,written E 1 ≈ bp E 2 ,if there exists a branching pomset bisimulation R ,such that(∅,∅)∈ R .
By replacing pomset transitions with steps,we can get the definition of branching step bisimulation.When PESs E 1 and E 2 are branching step bisimilar,wew rite E 1 ≈ bs E 2.
Definition 2.29
(Rooted branching pomset and step bisimulation).Assume a special termination predicate
 ,and let
√
represent a state with
√
,and let
√
represent a state with
√
 .Let
E
1
and
E
2
be PESs.A rooted branching pomset bisimulation is a relation
R⊆C
(
E
1
)
×C
(
E
2
),such that:
.Let
E
1
and
E
2
be PESs.A rooted branching pomset bisimulation is a relation
R⊆C
(
E
1
)
×C
(
E
2
),such that:
(1)If(
C
1
,
C
2
)∈
R
and
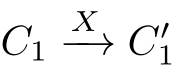 ,then
,then
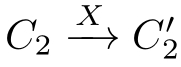 with
with
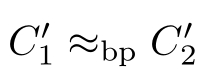 .
.
(2)If(
C
1
,
C
2
)∈
R
and
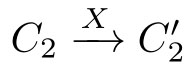 ,then
,then
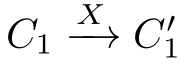 with
with
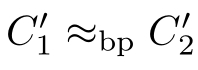 .
.
(3)If(
C
1
,
C
2
)∈
R
and
C
1
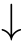 ,then
C
2
,then
C
2
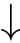 .
.
(4)If(
C
1
,
C
2
)∈
R
and
C
2
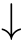 ,then
C
1
,then
C
1
 .
.
We say that E 1 and E 2 are rooted branching pomset bisimilar,written E 1 ≈ rbp E 2 ,if there exists a rooted branching pomset bisimulation R ,such that(∅,∅)∈ R .
By replacing pomset transitions with steps,we can get the definition of rooted branching step bisimulation.When PESs E 1 and E 2 are rooted branching step bisimilar,we write E 1 ≈ rbs E 2 .
Definition 2.30
(Branching(hereditary)history-p reserving bisimulation).Assume a special term ination predicate
 ,and let
√
represent a state with
√
,and let
√
represent a state with
√
 .A branching history-preserving(hp-)bisimulation isaposetalrelation
R⊆C
(
E
1
)
.A branching history-preserving(hp-)bisimulation isaposetalrelation
R⊆C
(
E
1
)
 C
(
E
2
),such that:
C
(
E
2
),such that:
(1)If(
C
1
,
f,C
2
)∈
R
and
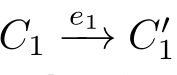 ,then
,then
①
e
1
≡τ,and(
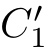 ,
f
[
e
1
,
f
[
e
1

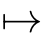 τ
],
C
2
)∈
R
;
τ
],
C
2
)∈
R
;
②There is a sequence of(zero or m ore)
τ
-transitions
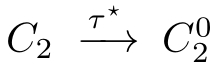 ,such that(
C
1
,
f,
,such that(
C
1
,
f,
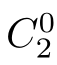 )∈
R
and
)∈
R
and
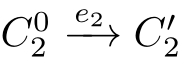 with(
with(
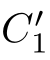 ,
f
[
e
1
,
f
[
e
1
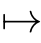 e
2
],
e
2
],
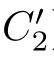 )∈
R
.
)∈
R
.
(2)If(
C
1
,
f,C
2
)∈
R
and
 ,then
,then
① X≡τ,and(
C
1
,
f
[
e
2

 τ
],
τ
],
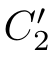 )∈
R
;
)∈
R
;
②There is a sequence of(zero or more)
τ
-transitions
 ,such that(
,such that(
 ,
f,C
2
)∈
R
and
,
f,C
2
)∈
R
and
 with(
with(
 ,
f
[
e
2
,
f
[
e
2
 e
1
],
e
1
],
 )∈
R
.
)∈
R
.
(3)If(
C
1
,
f,C
2
)∈
R
and
C
1
 ,then there is a sequence of(zero or more)
τ
transitions
,then there is a sequence of(zero or more)
τ
transitions
 such that(
C
1
,
f,
such that(
C
1
,
f,
 )∈
R
and
)∈
R
and
 .
.
(4)If(
C
1
,
f,C
2
)∈
R
and
C
2
 ,then there is a sequence of(zero or more)
τ
transitions
,then there is a sequence of(zero or more)
τ
transitions
 such that(
such that(
 ,
f,C
2
)∈
R
and
,
f,C
2
)∈
R
and
 .
.
E 1 and E 2 are branching history-preserving(hp-)bisimilar and are written as E 1 ≈ bhp E 2 ,if there exists a branching hp-bisimulation R such that(∅,∅,∅)∈ R .
A branching hereditary history-p reserving(hhp-)bisimulation is a downward closed branching hhp-bisimulation. E 1 and E 2 are branching hereditary historypreserving(hhp-)bisimilar and are written E 1 ≈ bhhp E 2 .
Definition 2.31
(Rooted branching(hereditary)history-preserving bisimulation).Assume a special term ination predicate
 ,and let
√
represent a state with
√
,and let
√
represent a state with
√
 .A rooted branching history-preserving(hp-)bisimulation is a posetal relation
R⊆
C
(
E
1
)
.A rooted branching history-preserving(hp-)bisimulation is a posetal relation
R⊆
C
(
E
1
)
 C
(
E
2
),such that:
C
(
E
2
),such that:
(1)If(
C
1
,
f,C
2
)∈
R
and
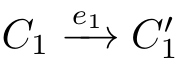 ,then
,then
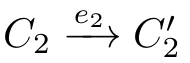 with
with
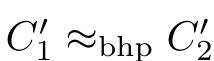 .
.
(2)If(
C
1
,
f,C
2
)∈
R
and
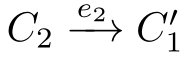 ,then
,then
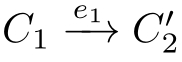 with
with
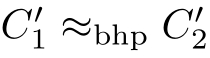 .
.
(3)If(
C
1
,
f,C
2
)∈
R
and
C
1
 ,then
C
2
,then
C
2
 .
.
(4)If(
C
1
,
f,C
2
)∈
R
and
C
2
 ,then
C
1
,then
C
1
 .
.
E 1 and E 2 are rooted branching history-preserving(hp-)bisimilar and are written as E 1 ≈ rbhp E 2 ,if there exists a rooted branching hp-bisimulation R such that(∅,∅,∅)∈ R .
A rooted branching hereditary history-preserving(hhp-)bisimulation is a downward closed rooted branching hhp-bisimulation. E 1 and E 2 are rooted branching hereditary history-preserving(hhp-)bisimilar and are written as E 1 ≈ rbhhp E 2 .
Definition 2.32
(Guarded linear recursive specification).A recursive specification is linear if its recursive equations are of the form:where
a
11
,···,
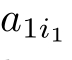 ,
a
k
1
,···,
,
a
k
1
,···,
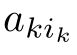 ,
b
11
,···,
,
b
11
,···,
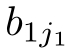 ,
,
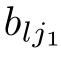 ,···,
,···,
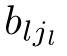 ∈E∪{
τ
},and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
∈E∪{
τ
},and the sum above is allowed to be empty,in which case it represents the dead lock
δ
.
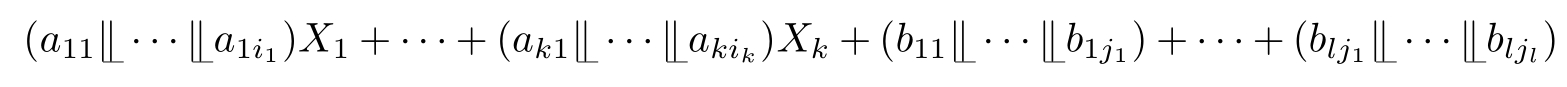
A linear recursive specification
E
is guarded if there does not exist an infinite sequence of
τ
-transitions〈 X|E〉
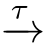 〈 X'|E〉
〈 X'|E〉
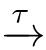 〈
X
''
|
E
〉
〈
X
''
|
E
〉
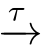 ···.
···.
The transition rules for τ are shown as follows,and the axioms of τ are shown in Table 2.5.
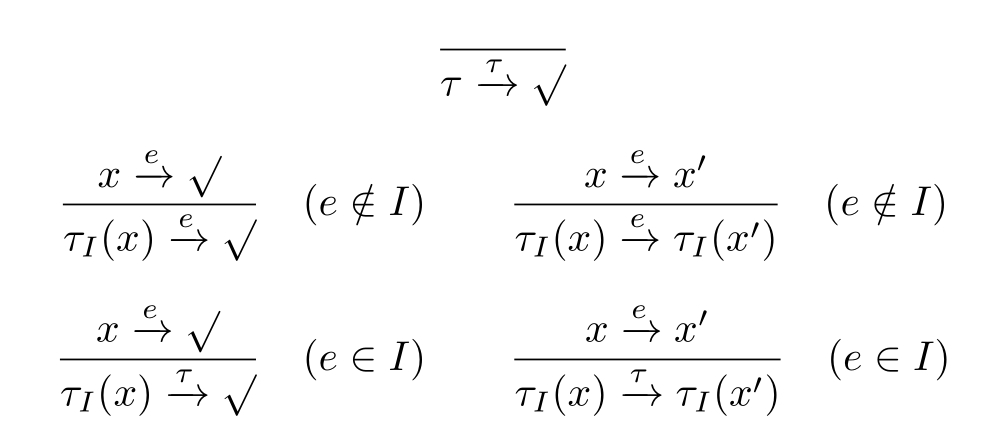
Table 2.5 The axioms of τ

Theorem 2.22 (Conservativity of APTC with silent step and guarded linear recursion).APTC with silent step and guarded linear recursion is a conservative extension of APTC with linear recursion.
Theorem 2.23 (Congruence theorem of APTC with silent step and guarded linear recursion).Rooted branching truly concurrent bisimu lation equivalences≈ rbp ,≈ rbs ,≈ rbhp ,and≈ rbhhp are all congruences with respect to APTC with silent step and guarded linear recursion.
Theorem 2.24 (Elimination theorem of APTC with silent step and guarded linear recursion).Each process term in APTC with silent step and guarded linear recursion isequal to a process term〈 X 1 | E 〉 with E being a guarded linear recursivespecification.
Theorem 2.25 (Soundness of APTC with silent step and guarded linear recursion).Let x and y be APTC with silent step and guarded linear recursion terms.If APTC with silent step and guarded linear recursion ├ x = y ,then
(1) x ≈ rbs y .
(2) x ≈ rbp y .
(3) x ≈ rbhp y .
(4) x ≈ rbhhp y .
Theorem 2.26 (Completeness of APTC with silent step and guarded linear recursion).Let p and q be closed APTC with silent step and guarded linear recursion terms,then
(1)If p ≈ rbs q ,then p = q .
(2)If p ≈ rbp q ,then p = q .
(3)If p ≈ rbhp q ,then p = q .
(4)If p ≈ rbhhp q ,then p = q .
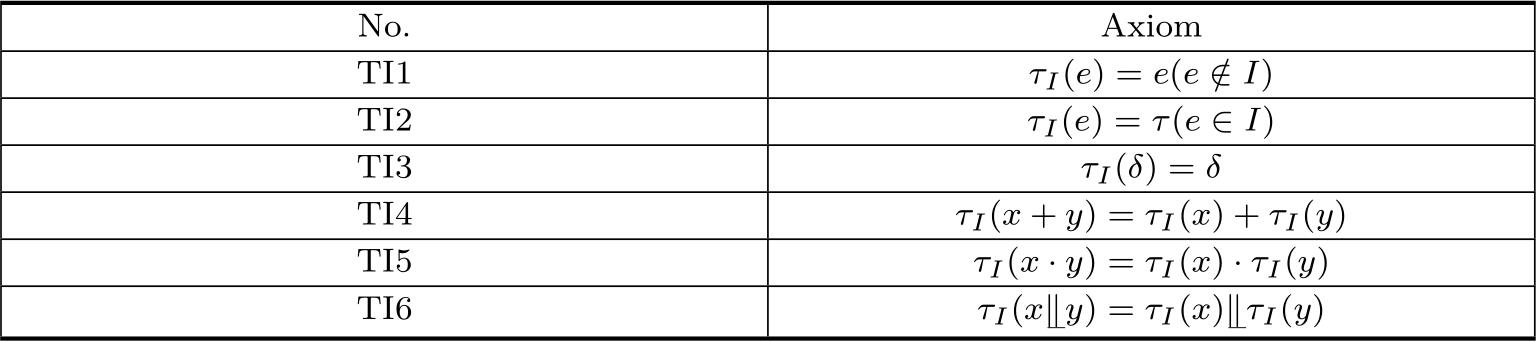
The axioms of abstraction operator are shown in Table 2.6.
Table 2.6 The axioms of abstraction operator
Theorem 2.27 (Conservativity of APTC τ with guarded linear recursion).APTC τ with guarded linear recursion is a conservative extension of APTC with silent step and guarded linear recursion.
Theorem 2.28 (Congruence theorem of APTC τ with guarded linear recursion).Rooted branching truly concurrent bisimulation equivalences≈ rbp ,≈ rbs ,≈ rbhp ,and≈ rbhhp are all congruences with respect to APTC τ with guarded linear recursion.
Theorem 2.29 (Soundness of APTC τ with guarded linear recursion).Let x and y be APTC τ with guarded linear recursion terms.If APTC τ with guarded linear recursion ├ x = y ,then
(1) x ≈ rbs y .
(2) x ≈ rbp y .
(3) x ≈ rbhp y .
(4) x ≈ rbhhp y .
Definition 2.33
(Cluster).Let
E
be a guarded linear recursive specification,and
I⊆
E.Two recursive variable
X
and
Y
in
E
are in the same cluster for
I
iffthere exist sequences of transitions
 and
and
 ,where
b
11
,···,
b
mi
,
c
11
,···,
c
nj
∈ I∪{τ}.
,where
b
11
,···,
b
mi
,
c
11
,···,
c
nj
∈ I∪{τ}.
a
1
 ···‖-
a
k
or(
a
1
···‖-
a
k
or(
a
1
 ···‖-
a
k
)
X
is an exit for the cluster
C
iff:①
a
1
···‖-
a
k
)
X
is an exit for the cluster
C
iff:①
a
1
 ···‖-
a
k
or(
a
1
···‖-
a
k
or(
a
1
 ···‖-
a
k
)
X
is a summand at the right-hand side of the recursive equation for a recursive variable in
C
;②in the case of(
a
1
···‖-
a
k
)
X
is a summand at the right-hand side of the recursive equation for a recursive variable in
C
;②in the case of(
a
1
 ···‖-
a
k
)
X
,either
a
l
/∈ I∪{τ}(
l
∈{1,2,···,
k
})or X/∈
C
.
···‖-
a
k
)
X
,either
a
l
/∈ I∪{τ}(
l
∈{1,2,···,
k
})or X/∈
C
.
Cluster fair abstraction rule is shown in Table 2.7.
Table 2.7 Cluster fair abstraction rule
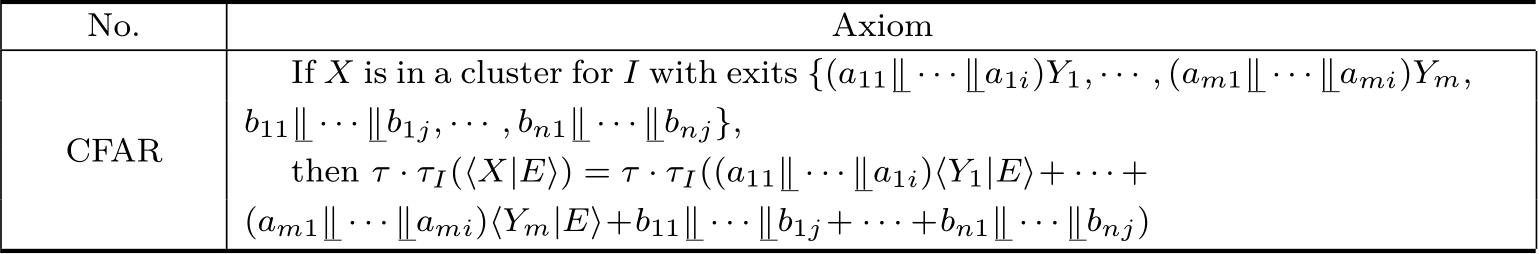
Theorem 2.30 (Soundness of CFAR).CFAR is sound modulo rooted branching tru ly concurrent bisimulation equivalences≈ rbs ,≈ rbp ,≈ rbhp ,and≈ rbhhp .
Theorem 2.31 (Completeness of APTC τ with guarded linear recursion and CFAR).Let p and q be closed APTC τ with guarded linear recursion and CFAR terms,then
(1)If p ≈ rbs q ,then p = q .
(2)If p ≈ rbp q ,then p = q .
(3)If p ≈ rbhp q ,then p = q .
(4)If p ≈ rbhhp q ,then p = q .
We introduce a constant called the shadow constantⓈto act as a placeholder that we ever used to deal entanglement in quantum process algebra.The transition rule for the shadow constantⓈis shown as follows.The rule states thatⓈcan terminate successfully without executing any action.
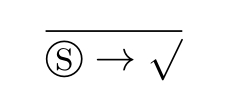
We will ad just the def inition of guarded linear recursive specification to the following one.
Definition 2.34
(Guarded linear recursivespecification).A linear recursivespecification
E
is guarded if there does not exist an infinite sequence of
τ
-transitions〈 X|E〉
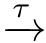 〈 X'|E〉
〈 X'|E〉
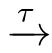 〈
X
''
|
E
〉
〈
X
''
|
E
〉
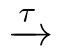 ···,and there does not exist an infinite sequence ofⓈ-transitions〈 X|E〉
···,and there does not exist an infinite sequence ofⓈ-transitions〈 X|E〉
 〈 X'|E〉
〈 X'|E〉
 〈
X
''
|
E
〉
〈
X
''
|
E
〉
 ···.
···.
Theorem 2.32 (Conservativity of APTC with respect to the shadow constant).APTC τ with guarded linear recursion and the shadow constant is a conservative extension of APTC τ .
We design the axioms for the shadow constantⓈin Table 2.8.And for
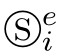 ,we introduce a superscrip t
e
to denote thatⓈbelongs to
e
,and a subscript
i
to denote that it is the
i
-th shadow of
e
.Moreover,we extend the set E to the set E∪{
τ
}∪{
δ
}∪{
,we introduce a superscrip t
e
to denote thatⓈbelongs to
e
,and a subscript
i
to denote that it is the
i
-th shadow of
e
.Moreover,we extend the set E to the set E∪{
τ
}∪{
δ
}∪{
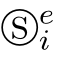 }.
}.
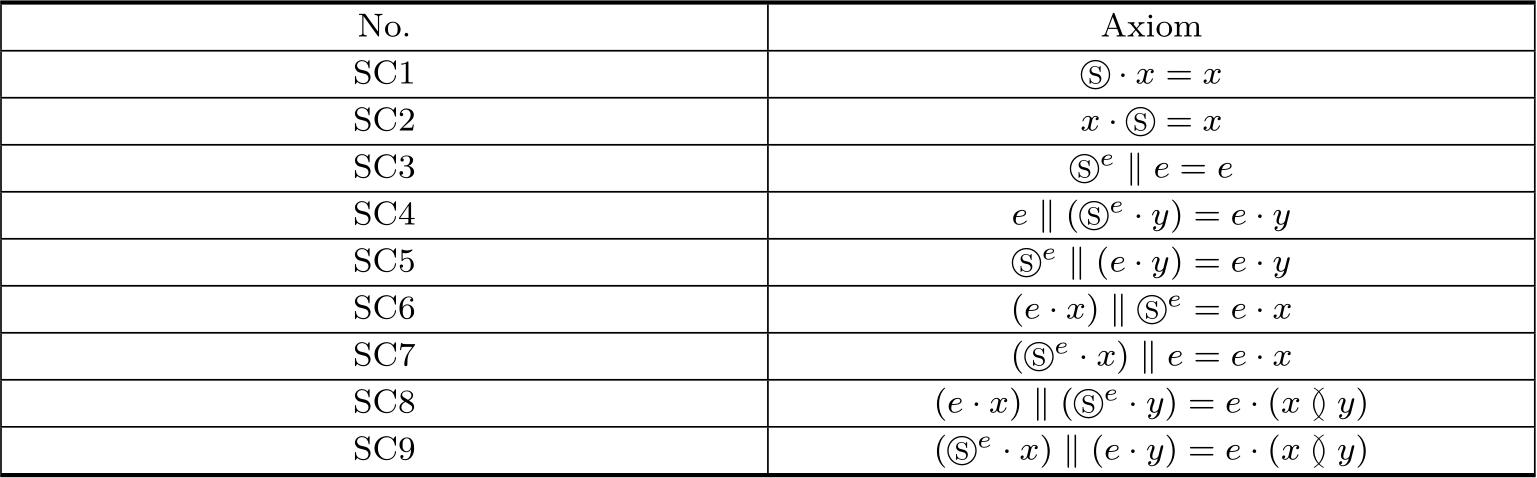
Table 2.8 The axioms of shadow constantⓈ
The m ismatch between an action and its shadows in parallelism can lead to a deadlock,that is,
e
‖
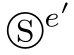 =
δ
with e/=
e'
.We must make all shadows
=
δ
with e/=
e'
.We must make all shadows
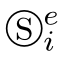 are distinct,to ensure
f
in hp-bisimulation is an isom orphism.
are distinct,to ensure
f
in hp-bisimulation is an isom orphism.
Theorem 2.33 (Soundness of the shadow constant).Let x and y be APTC τ with guarded linear recursion and the shadow constant terms.If APTC τ with guarded linear recursion and the shadow constant ├ x = y ,then
(1) x ≈ rbs y .
(2) x ≈ rbp y .
(3) x ≈ rbhp y .
Theorem 2.34 (Completeness of the shadow constant).Let p and q be closed APTC τ with guarded linear recursion,and CFAR,and the shadow constant terms,then
(1)If p ≈ rbs q ,then p = q .
(2)If p ≈ rbp q ,then p = q .
(3)If p ≈ rbhp q ,then p = q .
With the shadow constant,we have
∂
H
((
a·r
b
)≬
w
b
)=
∂
H
((
a·r
b
)≬(
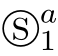 ·w
b
))=
a·c
b
·w
b
))=
a·c
b
where
H
={
r
b
,
w
b
}and
γ
(
r
b
,
w
b
)
 c
b
.
c
b
.
And we observe the following example:
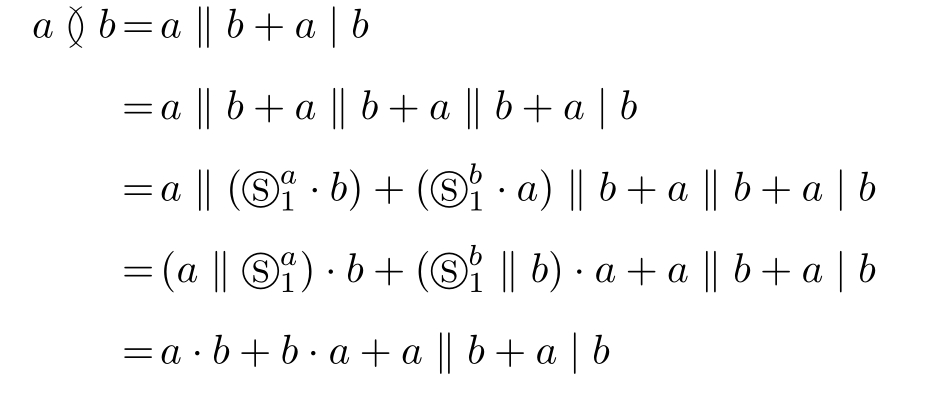
What do we observe?Yes,the parallelism contains both interleaving and true concurrency.Thismay be why true concurrency is called true concurrency.
APTC provides a formal framework based on tru ly concurrent behavioral sem antics,which can be used to verify the correctness of system behaviors.In this subsection,we tend to choose Alternating Bit Protocol(ABP) [10] .
The ABP isused to ensure the successful transm ission of data through a corrupted channel.This success isbased on the assum ption that data can be resent an unlim ited number of times,as illustrated in Figure 2.1.Then we alter the ABP into the true concurrency situation.
(1)Data elem ents d 1 , d 2 , d 3 ,···, d n from a finite setΔcommunicate between a Sender and a Receiver.
(2)If the Sender reads a datum from channel A 1 ,then this datum is sent to the Receiver in parallel through channel A 2 .
(3)The Sender processes the data inΔ,generates new data,and sends them to the Receiver through channel B .
(4)The Receiver receives thedata through channel B ,and sends them into channel C 2.
(5)If channel B is corrupted,them essage communicated through channel B can be turned into an errormessage⊥.
(6)Every time the Receiver receives a message through channel B ,it sends an acknow ledgem ent to the Sender through channel D ,which is also corrupted.
(7)Finally,the Sender and the Receiver send out their outputs in parallel through channels C 1 and C 2 .
In the truly concurrent ABP,the Sender sends its data to the Receiver,and the Receiver can also send its data to the Sender.However,for simplicity and without loss of generality,we will assume that only the Sender sends itsdata,and the Receiver just receives the data from the Sender.The Sender attaches a bit 0 to data elements d 2 k- 1 and a bit 1 to data elem ents d 2 k ,when they are sent into channel B .When the Receiver reading a datum,it sends back the attached bit via channel D .If the Receiverreceives a corrupted message, then it sends back the previous acknowledgement to the Sender.
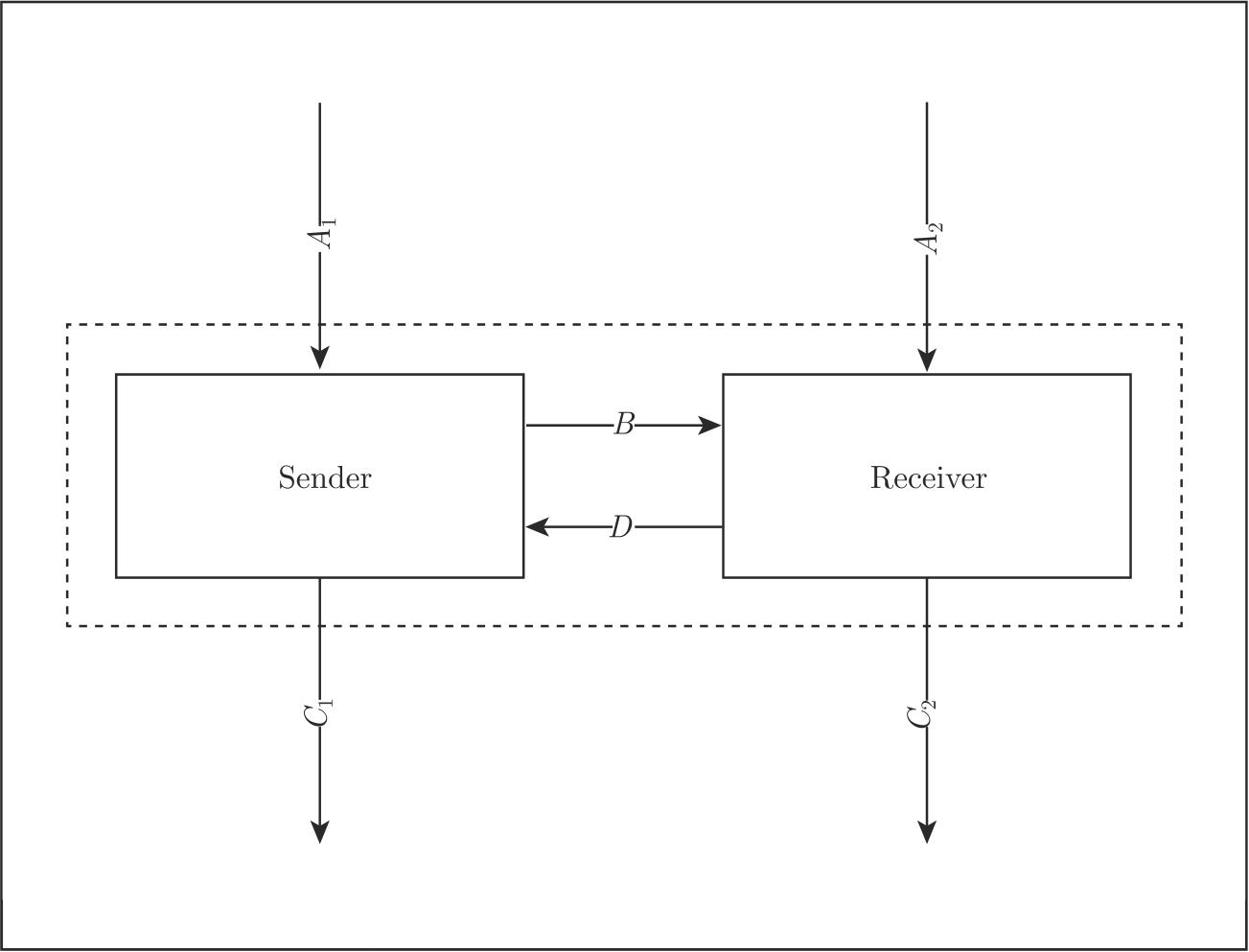
Figure 2.1 Alternating bit protocol
Then the state transition of the Sender can be described by APTC as follows:
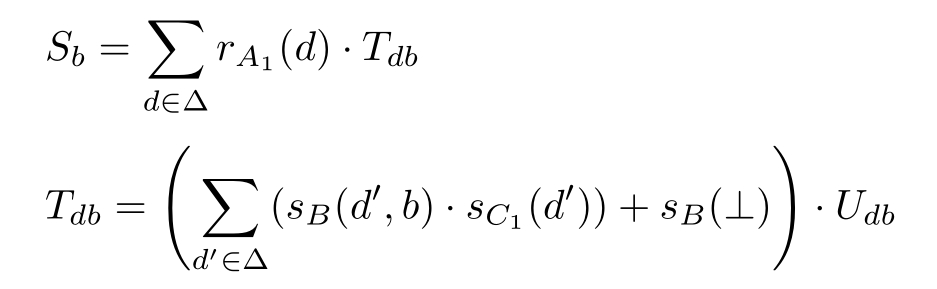
U db = r D ( b ) ·S 1 -b +( r D (1 -b )+ r D (⊥)) ·T db
where s B denotes sending data through channel B , r D denotes receiving data through channel D ,similarly, r A 1 denotes receiving data through channel A 1 , s C 1 denotes sending data through channel C 1 ,and b ∈{0,1}.
And the state transition of the Receiver can be described by APTC as follows:
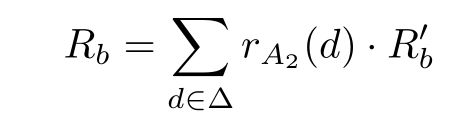
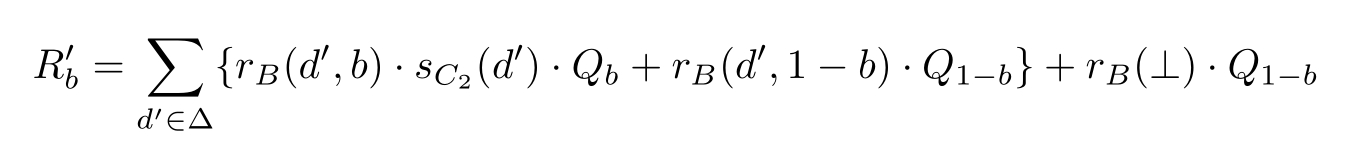
Q b =( s D ( b )+ s D (⊥)) ·R 1 -b
where r A 2 denotes receiving data through channel A 2 , r B denotes receiving data through channel B , s C 2 denotes sending data through channel C 2 , s D denotes sending data through channel D ,and b ∈{0,1}.
The send action and receive action of the same data through the same channel can communicate with each other,other wise,a dead lock δ will be caused.We define the following communication functions:
γ ( s B ( d',b ), r B ( d',b ))≜ c B ( d',b )
γ ( s B (⊥), r B (⊥))≜ c B (⊥)
γ ( s D ( b ), r D ( b ))≜ c D ( b )
γ ( s D (⊥), r D (⊥))≜ c D (⊥)
Let R0 and S0 be in parallel,then the system R0S0 can be represented by the following process term:
τ I ( ∂ H ( Θ ( R0 ≬ S0 )))= τ I ( ∂ H ( R0 ≬ S0 ))
where H ={ s B ( d',b ), r B ( d',b ), s D ( b ), r D ( b )| d' ∈Δ, b ∈{0,1 }}∪{s B (⊥), r B (⊥), s D (⊥), r D (⊥)}
I ={ c B ( d',b ), c D ( b )| d' ∈Δ, b ∈{0,1 }}∪{c B (⊥), c D (⊥)}.
Then we get the following conclusion.
Theorem 2.35 (Correctness of the ABP).The ABP τ I ( ∂ H ( R0 ≬ S0 ))can exhibit the desired external behaviors.
Proof: By using the algebraic laws of APTC,we can derive the following expansions:
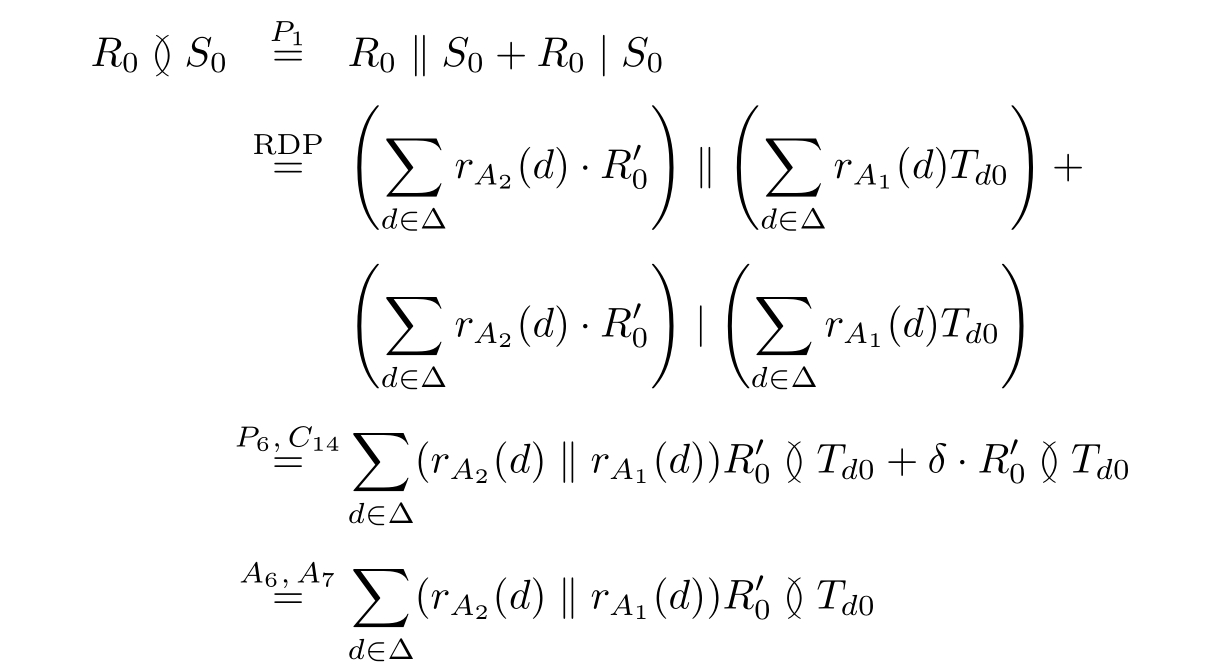
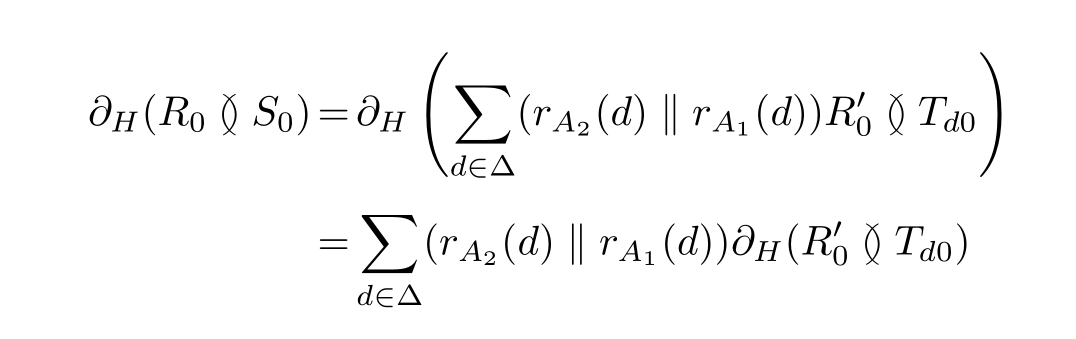
Similarly,we can get the following equations.
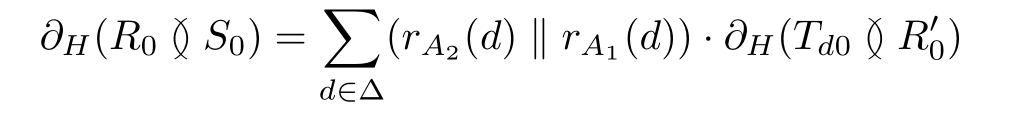
∂
H
(
T
d
0
≬
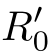 )=
c
B
(
d',
0)·(
)=
c
B
(
d',
0)·(
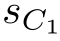 (
d'
)‖
(
d'
)‖
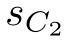 (
d'
))
·∂
H
(
U
d
0
≬
Q0
)+
c
B
(⊥)
·∂
H
(
U
d
0
≬
Q
1
)
(
d'
))
·∂
H
(
U
d
0
≬
Q0
)+
c
B
(⊥)
·∂
H
(
U
d
0
≬
Q
1
)
∂ H ( U d 0 ≬ Q 1 )=( c D (1)+ c D (⊥)) ·∂ H ( T d 0 ≬ R'0 )
∂
H
(
Q0
≬
U
d
0
)=
c
D
(0)
·∂
H
(
R
1
≬
S
1
)+
c
D
(⊥)
·∂
H
(
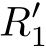 ≬
T
d
0
)
≬
T
d
0
)
∂
H
(
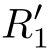 ≬
T
d
0
)=
(
c
B
(
d',
0)+
c
B
(⊥))
·∂
H
(
Q0
≬
U
d
0
)
≬
T
d
0
)=
(
c
B
(
d',
0)+
c
B
(⊥))
·∂
H
(
Q0
≬
U
d
0
)
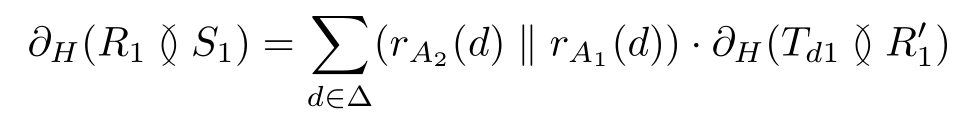
∂
H
(
T
d
1
≬
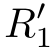 )=
c
B
(
d',
1)·(
)=
c
B
(
d',
1)·(
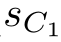 (
d'
)‖
(
d'
)‖
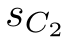 (
d'
))
·∂
H
(
U
d
1
≬
Q
1
)+
c
B
(⊥)
·∂
H
(
U
d
1
≬
(
d'
))
·∂
H
(
U
d
1
≬
Q
1
)+
c
B
(⊥)
·∂
H
(
U
d
1
≬
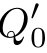 )
)
∂
H
(
U
d
1
≬
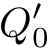 )=(
c
D
(0)+
c
D
(⊥))
·∂
H
(
T
d
1
≬
)=(
c
D
(0)+
c
D
(⊥))
·∂
H
(
T
d
1
≬
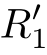 )
)
∂
H
(
Q
1
≬
U
d
1
)=
c
D
(1)
·∂
H
(
R0
≬
S0
)+
c
D
(⊥)
·∂
H
(
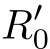 ≬
T
d
1
)
≬
T
d
1
)
∂
H
(
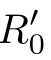 ≬
T
d
1
)=(
c
B
(
d',
1)+
c
B
(⊥))
·∂
H
(
Q
1
≬
U
d
1
)
≬
T
d
1
)=(
c
B
(
d',
1)+
c
B
(⊥))
·∂
H
(
Q
1
≬
U
d
1
)
Let ∂ H ( R0 ≬ S0 )=〈 X 1 | E 〉,where E is the following guarded linear recursive specification:
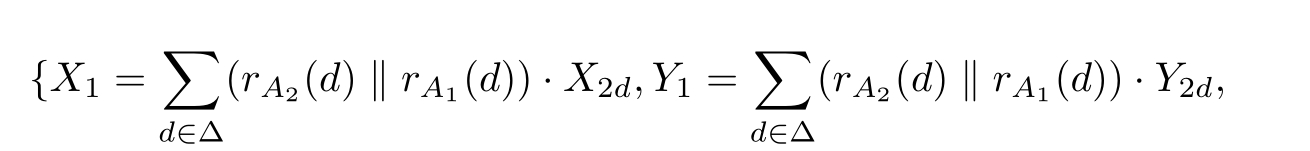
X 2 d = c B ( d', 0) ·X 4 d + c B (⊥) ·X 3 d , Y 2 d = c B ( d', 1) ·Y 4 d + c B (⊥) ·Y 3 d ,
X 3 d =( c D (1)+ c D (⊥)) ·X 2 d , Y 3 d =( c D (0)+ c D (⊥)) ·Y 2 d ,
X 4 d =( s C 1 ( d' ) ‖s C 2 ( d' )) ·X 5 d , Y 4 d =( s C 1 ( d' ) ‖s C 2 ( d' )) ·Y 5 d ,
X 5 d = c D (0) ·Y 1 + c D (⊥) ·X 6 d , Y 5 d = c D (1) ·X 1 + c D (⊥) ·Y 6 d ,
X 6 d =( c B ( d, 0)+ c B (⊥)) ·X 5 d , Y 6 d =( c B ( d, 1)+ c B (⊥)) ·Y 5 d | d,d' ∈Δ}
Then we app ly the abstraction operator τ I to〈 X 1 | E 〉.
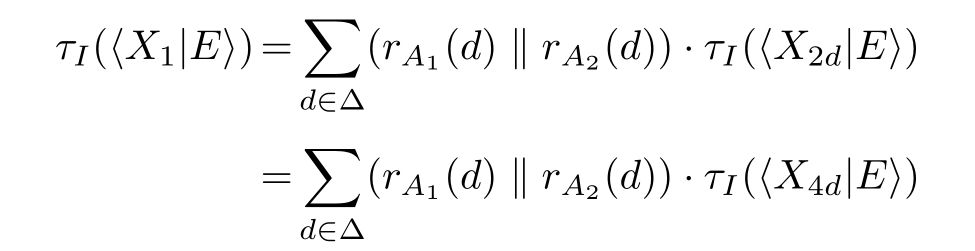
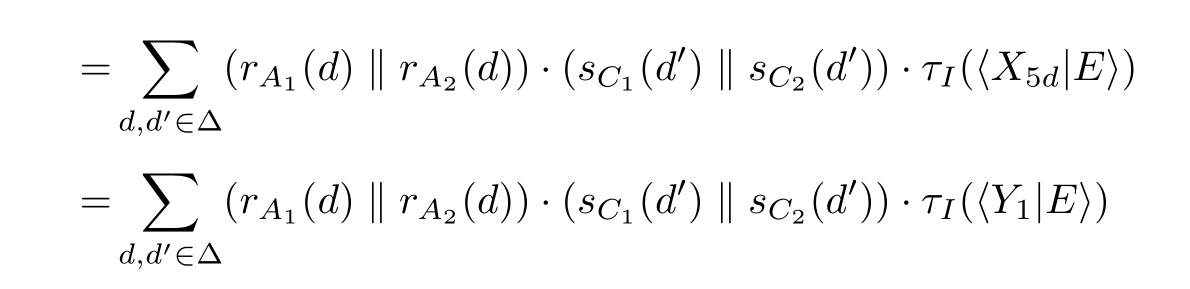
Similarly,we can get
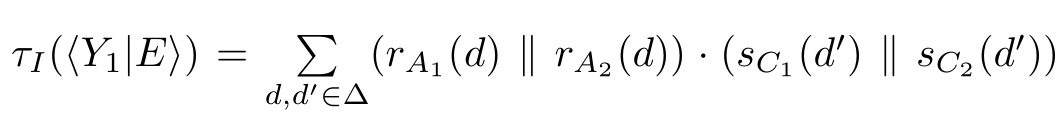 ·τ
I
(〈
X
1
|
E
〉).We get
τ
I
(
∂
H
(
R0
≬
S0
))
·τ
I
(〈
X
1
|
E
〉).We get
τ
I
(
∂
H
(
R0
≬
S0
))
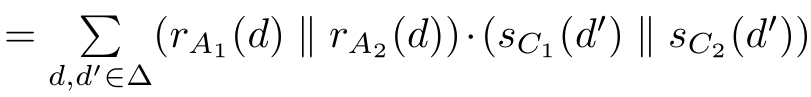 ·τ
I
(
∂
H
(
R0
≬
S0
)).So,the ABP
τ
I
(
∂
H
(
R0
≬
S0
))can exhibit the desired external behaviors.
·τ
I
(
∂
H
(
R0
≬
S0
)).So,the ABP
τ
I
(
∂
H
(
R0
≬
S0
))can exhibit the desired external behaviors.
With the help of the shadow constant,we can now verify the traditional ABP[10].
The ABP is used to ensure successful transmission of data through a corrupted channel.This success is based on the assumption that data can be resent an unlimited number of times,as illustrated in Figure 2.2,we alter the ABP into the true concurrency situation.
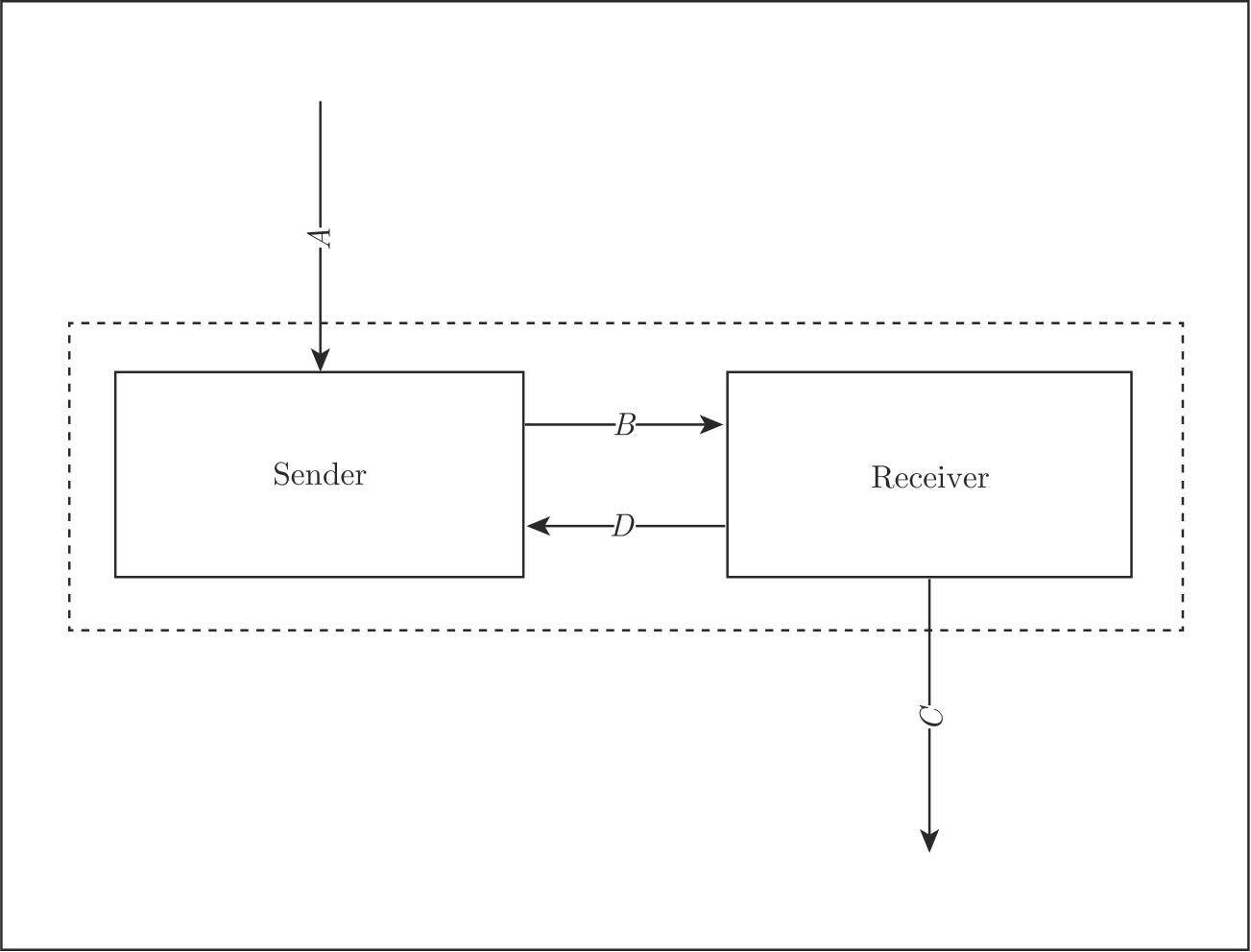
Figure 2.2 Alternating bit protocol
(1)Data elements d 1 , d 2 , d 3 ,···, d n from a finite set Δ are communicated between a Sender and a Receiver.
(2)The Sender reads a datum from channel A .
(3)The Sender processes the data inΔ,formes new data,and sends them to the Receiver through channel B .
(4)The Receiver sends the datum to channel C .
(5)If channel B is corrupted,them essage communicated through channel B can be turned into an error message⊥.
(6)Every time the Receiver receives a message through channel B ,it sends an acknowledgement to the Sender through channel D ,which is also corrupted.
The Sender attaches a bit 0 to data elem ents d 2 k- 1 and a bit 1 to data elem ents d 2 k ,when they are sent into channel B .When the Receiver reads a datum,it sends back the attached bit through channel D .If the Receiver receives a corrupted message,then it sends back the previous acknowledgement to the Sender.
Then the state transition of the Sender can be described by APTC as follows.
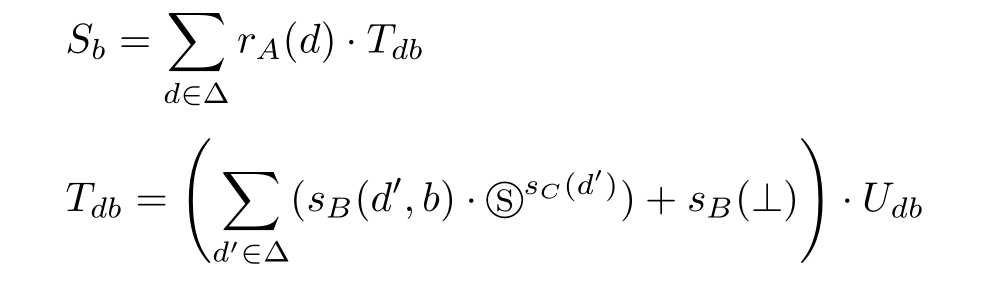
U db = r D ( b ) ·S 1 -b +( r D (1 -b )+ r D (⊥)) ·T db
where
s
B
denotes sending data through channel
B
,
r
D
denotes receiving data through channel
D
,similarly,
r
A
denoted receiving data through channel
A
,
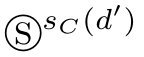 denotes the shadow of
s
C
(
d'
).
denotes the shadow of
s
C
(
d'
).
The state transition of the Receiver can be described by APTC as follows:
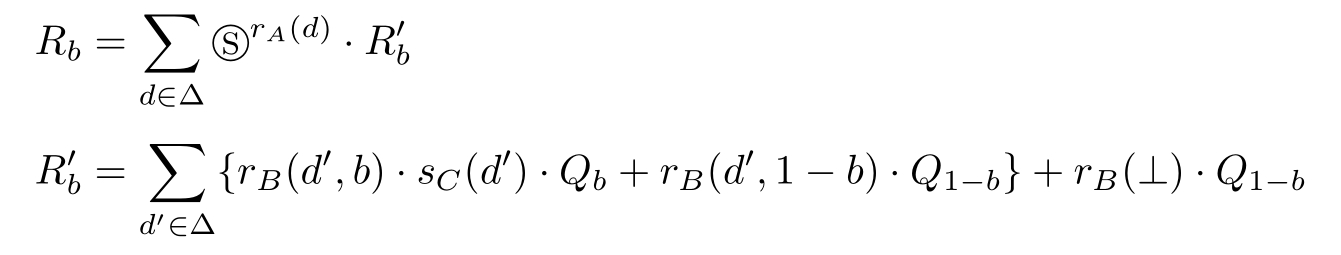
Q b =( s D ( b )+ s D (⊥)) ·R 1 -b
where Ⓢ r A ( d ) denotes the shadow of r A ( d ), r B denotes receiving data through channel B , s C denotes sending data through channel C , s D denotes sending data through channel D ,and b ∈{0,1}.
The sending action and receiving action of the same data through the same channel can communicate with each other,other wise,a dead lock δ will be caused.We define the following communication functions:
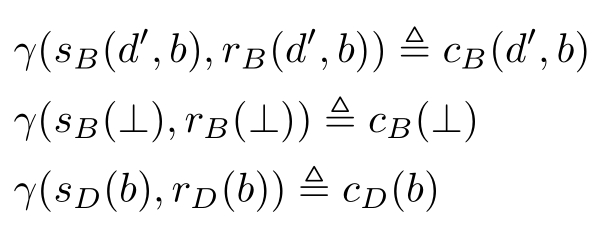
γ ( s D (⊥), r D (⊥))≜ c D (⊥)
Let R0 and S0 be in parallel,then the system R0S0 can be represented by the following process term:
τ I ( ∂ H ( Θ ( R0 ≬ S0 )))= τ I ( ∂ H ( R0 ≬ S0 ))
where H ={ s B ( d',b ), r B ( d',b ), s D ( b ), r D ( b )| d' ∈Δ, b ∈{0,1 }}∪{s B (⊥), r B (⊥), s D (⊥), r D (⊥)}
I ={ c B ( d',b ), c D ( b )| d' ∈Δ, b ∈{0,1}} ∪ { c B (⊥), c D (⊥)}.
Then we get the following conclusion.
Theorem 2.36 (Correctness of the ABP).The ABP τ I ( ∂ H ( R0 ≬ S0 ))can exhibit the desired external behaviors.
Proof:
Similarly,we can get
τ
I
(〈
X
1
|
E
〉)=
 r
A
(
d
)
·s
C
(
d'
)
·τ
I
(〈
Y
1
|
E
〉),and
τ
I
(〈
Y
1
|
E
〉)=
r
A
(
d
)
·s
C
(
d'
)
·τ
I
(〈
Y
1
|
E
〉),and
τ
I
(〈
Y
1
|
E
〉)=
 r
A
(
d
)
·s
C
(
d'
)
·τ
I
(〈
X
1
|
E
〉).
r
A
(
d
)
·s
C
(
d'
)
·τ
I
(〈
X
1
|
E
〉).
So,the ABP τ I ( ∂ H ( R0 ≬ S0 ))can exhibit the desired external behaviors.