




In this subsection,we introduce concepts and conclusions about elimination,which are very important in the proof of the completeness theorem.
Definition 2.12 (Elimination property).Let a process algebra with a defined set of basic terms as a subset of the set of closed terms over the process algebra.Then the process algebra has the elimination to basic terms property if for every closed term s of the algebra,there exists a basic term t of the algebra such that the algebra ├ s = t .
Definition 2.13 (Strongly normalizing).A term s0 is called strongly normalizing if it does not have an infinite series of reductions beginning with s0 .
Definition 2.14.
We w rite
s>
lpo
t
if
s
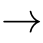 +
t
,where
+
t
,where
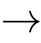 +
is the transitive closure of the reduction relation defined by the transition rules of an algebra.
+
is the transitive closure of the reduction relation defined by the transition rules of an algebra.
Theorem 2.2
(Strong normalization).Let a Term Rewriting System(TRS)with finitely many rewriting rules and let
>
be a well-founded ordering on the signature of the corresponding algebra.If
s>
lpo
t
for each rewriting rule
s
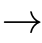 t
in the TRS,then the term rewriting system is strongly normalizing.
t
in the TRS,then the term rewriting system is strongly normalizing.