




Control theory traditionally deals with the dynamic behaviors of processes,which are captured by differential equations.With the rapid usage of computer based control,discrete event processes and hybrid processes have emerged.
Discrete Event Processes(DEPs)may be the simplest processes that exhibit the discrete behaviors.In DEPs,the states are discrete and the state transitions occur only in response to discrete events.There are minor differences between DEPs and computational processes,except for parallelism and concurrency.For most computational properties,such as sequentiality,non-determinism,recursion and abstraction,they are the same.
Hybrid theory is a hybrid of system theory and computer science.In system theory,the system behaviors are usually captured by differential equations and inclusions,which are in the form of flow clauses for continuous behaviors and re-initialization clauses for discontinuous behaviors.While in computer science,the system behaviors are usually captured by a set of discrete atomic actions and the computational logics among them,as process algebra does.
We follow the conventions of describing hybrid systems in Reference[1]in the following.
Physical behaviors are provided by describing how the model variable
V
m
evolves through time
T
.
V
(
x
)is the domain of model variable
x
∈
V
m
and is specif ied at the modeling phase.While
V
=
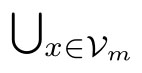 V
(
x
)denotes the union of all variable domains and Val=
V
m
V
(
x
)denotes the union of all variable domains and Val=
V
m
 V
denotes the set of variable evaluations.The set of all flows is denoted by
F
={
f
∈
T
V
denotes the set of variable evaluations.The set of all flows is denoted by
F
={
f
∈
T
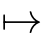 Val|dom(
f
)=[0,
t
]}for some
t
∈
T
,where dom(
f
)is the domain of
f
.The flows described by a flow predicate are called the solution of that predicate,and the set of flow predicates is denoted by
P
f
,and
P
f
∈P
f
.
Val|dom(
f
)=[0,
t
]}for some
t
∈
T
,where dom(
f
)is the domain of
f
.The flows described by a flow predicate are called the solution of that predicate,and the set of flow predicates is denoted by
P
f
,and
P
f
∈P
f
.
Definition 1.1 (Solution of a flow clause).A pair( v,σ )∈Val ×F is a solution of a flow clause c ∈ C ,denoted as( v,σ )⊨ c ,satisfies:
(1)(
v,σ
)⊨
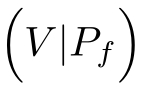 if
σ
⊨
f
P
f
,and
∀x
∈
V
and
V
⊆
V
m
,
v
(
x
)
-σ
(0)(
x
).
if
σ
⊨
f
P
f
,and
∀x
∈
V
and
V
⊆
V
m
,
v
(
x
)
-σ
(0)(
x
).
(2)( v,σ )⊨ c and( v,σ )⊨ c' ,then( v,σ )⊨ c∧c' .
Re-initialization predicates describe a set of re-initializations Val
×
Val denoted
R
,such re-initializations are called solutions of the re-initialization predicates,and the set of re-initialization predicates is denoted by
P
r
and
P
r
∈
P
r
.We use the set of re-initialization predicates
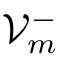 ={
x
-
|
x
∈
V
m
}and
={
x
-
|
x
∈
V
m
}and
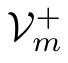 ={
x
+
|
x
∈
V
m
}to model the current and future values of a model variable.
={
x
+
|
x
∈
V
m
}to model the current and future values of a model variable.
Definition 1.2 (Solution of a re-initialization clause).A pair( v,v' )∈ R is a solution of a re-initialization clause d ∈ D where D is the set of re-initialization clauses and Σ is the set of flow labels,denoted as( v,v' )⊨ d ,satisf ies:
(1)( v,v' )⊨[ V|P r ] if( v,v' )⊨ r P r ,and ∀x ∈ /V , v ( x )= v' ( x ).
(2)( v,v' )⊨ d'∨d '' if( v,v' )⊨ d' ,or( v,v' )⊨ d '' .
(3)( v,v' )⊨ d'∧d '' if( v,v' )⊨ d' ,and( v,v' )⊨ d '' .
(4)( v,v' )⊨ d'~d '' if ∃ν ∈Val,( v,ν )⊨ d' ,and( v,ν )⊨ d '' .
(5)( v,v' )⊨ d ' ? if v = v' and ∃ν ∈Val with( v,ν )⊨ d' .
(6)( v,v' )⊨ c jmp if ∃σ ∈ Σ with( v,σ )⊨ c and σ (0)= v' .
where d ? is a satisf iability operator on clauses d ∈ D , c jmp is a re-initialization clause derived from a flow clause c ∈ C ,which executes the same discontinuities that are allowed initially by the flow clause.
The well-known process algebras,such as CCS [2][3] ,ACP [4] and π -calculus [5][6] ,capture the interleaving concurrency based on bisimilarities semantics.We have done some works on truly concurrent process algebras,such as CTC [7] ,APTC [7] and π tc [7] ,which capture true concurrency based on truly concurrent bisimilarities,such as pomset bisimilarities,step bisimilarities,history-preserving(hp-)bisimilarities and hereditary history-preserving(hhp-)bisimilarities.Truly concurrent process algebras are generalizations of the corresponding traditional process algebras.
In this book,we introduce discrete event systems and hybrid systems into truly concurrent process algebras,based on the work on discrete event processes [8] and hybrid process algebra [1] .We introduce the preliminaries in Chapter 2.An axiomatization of discrete event processes is presented in Chapter 3 and an axiomatization of distributed discrete event processes is discussed in Chapter 4.Hybrid APTC and its applications in modelling neural networks are covered in Chapter 5,and hybrid APTC with localities and its app lications in modeling distributed/federated neural networks are exp lored in Chapter 6.
Note that this book is one of Beijing University of Technology Graduate Innovation Education Series Textbooks.