





1946—1948年间,我在芝加哥大学物理系做了两年半研究生。费米(Enrico Fermi,1901—1954)那个时候常常跟我们几个研究生到饭堂(cafeteria)去吃午饭。参加这些午饭的经常有Goldberger,Chew,Chamberlain,Joan Hinton(寒春)和我,后来Rosenbluth和李政道等人也加入了。大约是1948年的一天,费米带了一位矮矮的、瘦瘦的法国人到饭堂,那天多半是费米和那位法国人交谈。事后我们问费米他是何许人,费米说,他是韦伊(André Weil,1906—1998),是重要的数学家。费米还说,那天韦伊主要是讲他猜想物理学家的一些新粒子可能与几何学/拓扑学里面出现的一些分类现象有关。
当时我们都没有懂韦伊的意思。我现在想,那天韦伊到芝加哥大学访问,可能是要和芝加哥大学数学系当时的系主任Stone讨论他到芝大的事情。后来,果然韦伊和陈省身先后接受了Stone的邀请,创建了芝大数学系20世纪50年代的辉煌十年。

1960年前后,陈先生西去伯克利,韦伊东去普林斯顿的高等研究院。陈先生告诉我,韦伊说陈先生西去是为了离中国近一些,他自己东去是为了离法国近一些。
韦伊和我在高等研究院以后同事了五六年。我们不同行,很少有交流的机会,所以我始终没有和他讨论过十多年前他和费米那天谈话的内容。
70年代我了解了规范场与数学家的纤维丛的密切关系,了解了美妙的陈氏级,写了一首诗《赞陈氏级》:
天衣岂无缝,匠心剪接成。
浑然归一体,广邃妙绝伦。
造化爱几何,四力纤维能。
千古寸心事,欧高黎嘉陈。

我也了解了深邃的Chern-Weil定理,从而自然地想起芝大的那一顿午饭时韦伊所讲的可能就是陈氏级等几何/拓扑学中出现的示性类。韦伊的这个猜想:把陈氏级等几何观念和物理中的一些量子数连起来有没有可能是对的呢?我想很有可能:物理世界的基本结构是几何的,这是爱因斯坦再三强调的,也是今天许多理论物理学家所坚信的。而且 整体 微分几何中出现陈氏级等现象,与玻尔在 圆周 上创设量子化条件(如前页图)其 精神是非常相似的 。韦伊的猜想其实是很自然的。
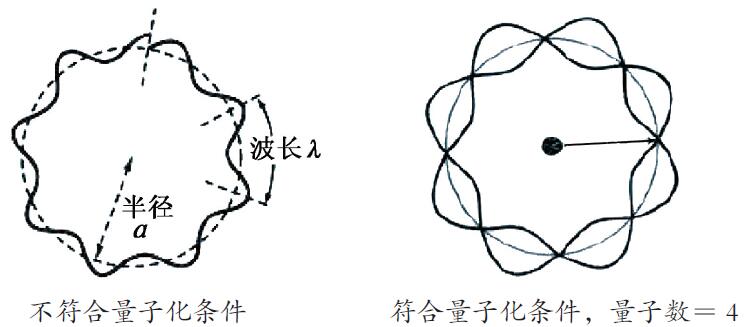
玻尔的量子化条件的德布罗意解释。
左图:圆周上波动数不是整数;
右图:圆周上波动数是整数4(此二图转载自Google网站)。
20世纪70年代规范场与纤维丛的密切关系震惊了数学界。对此新发展陈先生当然非常高兴,他曾在一次谈话中讲过一个故事,这个故事后来传闻很多,多半不可信。当时的记录是这样的,陈先生说:
有一年我跟内人去参观罗汉塔,我就感慨地跟她说:“无论数学做得怎么好,顶多是做个罗汉。”菩萨或许大家都知道他的名字,罗汉谁也不知道那个是哪个人。所以不要把名看得太重。Riemann的工作为什么重要呢?因为数学跟其他的科学一样要不断扩充范围,大家重视的工作,都是开创性的工作。

我解读这段文字如下:陈先生当时认为自己是罗汉,还不是菩萨。这是不是表示他过于谦让呢?我不是数学家,不能评说。但是如果韦伊1948年的猜想是对的,那么陈先生的开创性的陈氏级等数学工作的重要性就要旁及物理世界的最最基本的结构了,那时数学仙山上的大雄宝殿中岂能不迎来一尊新菩萨?