下载掌阅APP，畅读海量书库
立即打开
三个主旋律全部都是20世纪最初几十年里引入的。它们在20世纪剩下的岁月中所发挥的作用和音乐中主旋律的作用非常类似：经历展开、变奏和回旋。
40年代后期，宇宙射线实验中发现了许多新粒子。因为它们出乎人们的意料，所以被称为“奇异粒子”。这些奇异粒子之间，以及它们和已知粒子之间的相互作用，自然成为讨论的话题。有几年，这些讨论都是遵循着这样的思路：写出洛伦兹变换下不变的耦合常数，比如标量介子具有矢量耦合常数，矢量介子具有张量耦合常数，等等，并求出每种可能性的可观测结果。这样的概念缺乏一个原理，一个普遍的相互作用原理。1954年，杨振宁和米尔斯试图通过推广外尔的电磁学规范理论来阐述这样一个原理。他们注意到，根据外尔的理论，电荷守恒和一种不变性相关联：规范不变性，或者规范对称。因此，那时广泛讨论的另一种守恒定律，同位旋守恒，也许应该和一种普遍的规范不变性或者规范对称有关。下面引用他们1954年论文中的原话：
同位旋的守恒表明存在着像电荷守恒定律那样的一种基本的不变性定律。在电荷守恒定律的情形中，电荷充当着电磁场的源；而在同位旋守恒的情形中，一个重要的概念是规范不变性，与之密切相关的有（1）电磁场的运动方程，（2）电流密度的存在，以及（3）带电场和电磁场之间可能的相互作用。我们尝试着将这一规范不变性的概念进行推广，把它应用到同位旋守恒定律上。结果表明，一种自然而然的推广是有可能实现的。
这一自然的推广就是后来的杨—米尔斯理论，或者叫作非阿贝尔规范理论。
还有另外一种方法也同样可以实现推广，那就是杨振宁和米尔斯在1954年的另一篇文章的摘要中一开始就指出的：
本文指出，通常的同位旋不变性原理和局域场的概念有不一致之处。
这句话有点夸大其词。应该换成如下的说法：
本文指出，通常的同位旋不变性原理和局域场概念的精神相违背。
两种实现推广的方法都强调不变性，即对称性。相位因子当然也在考虑范围之内（它的整个发展就是一部量子力学理论），但那时它还不是推广的关键所在。尤其是外尔重点考虑的伸展因子（变换为相位因子）没有得到相应的推广处理，只是到了1974年，它才最终得以推广，并被称为不可积非阿贝尔相位因子。
有了不可积相位因子，对称和相位因子这两个主旋律的回旋就变得和谐而自然了。回顾这一历史，令人感到惊讶的是，这两个主题深得外尔一辈子的喜爱。不幸的是，在他1955年去世的时候，他没能亲眼看到自己的概念所结出的累累硕果。他在1949年的时候曾这样评价自己：
赫尔曼·外尔——苏黎世一匹孤独的狼——也曾在这一领域忙碌；但不幸的是，他总是把他的数学和物理的以及哲学的猜想混为一谈。
今天，我们应当说他的猜想具有惊人的洞察力，它们促使物理学史的进程发生了改变。
非阿贝尔规范理论在20世纪50年代并没有给物理学界留下深刻的印象。该理论是仿照电磁学建立起来的。按照电磁学理论，诸如光子之类的矢量玻色子其质量为零，因此大家普遍认为在非阿贝尔规范理论中，矢量玻色子的质量亦为零。而这样的介子既然在实验上尚未被发现，该理论也就不具有说服力了。1954年，杨和米尔斯在论文的最后一段中讨论了这个问题，并总结说：
在电动力学中，人们根据电荷守恒的要求得出了光子质量为零的结论。但在b场情形中不能做出相应的论证，尽管同位旋守恒定律依然成立。所以，关于b量子的质量我们没能得出什么结论。
然后到了60年代，好几个物理学家提出了一种有关对称性的重要的新观念，即对称破缺。按照这种观念，在数学形式体系中可以有完美的对称，但同时也允许物理现象中存在对称破缺。这样一来，非阿贝尔规范理论中的矢量玻色子就有可能具有非零的质量。从70年代初期开始，无论是在实验上还是在理论上，这一观念都受到了大力推崇，并导致了我们现在所谓的标准模型的诞生，该模型在描述粒子物理的大量实验结果方面取得了极大的成功。
在非阿贝尔规范理论中，相互作用取决于对称性（即关于规范变换的不变性）。因此有了这一原理：对称性决定相互作用。它可以说是采用了爱因斯坦—闵可夫斯基—爱因斯坦旋律，后者早先曾经通过坐标变换下的不变性要求来决定引力相互作用。
虽然标准模型取得了极大的成功，但它有个重大缺点：对称破缺的应用方式太特殊，而且不是唯一的。所以，没有几个物理学家相信标准模型是最终的理论。这个问题，连同广义相对论和量子理论之间缺乏成功结合的问题，到20世纪末依旧是物理学的基本问题。
量子化、对称性和相位因子这三个主旋律漂亮而微妙地交织于费曼的路径积分体系之中，而对于非阿贝尔规范理论，再加上一条限制，即被积函数是一个时序乘积（timeordered product）
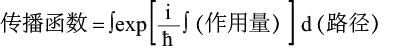（3）
对非阿贝尔规范理论：量子化通过作用量子
ħ
的存在而成为一个重要组成部分；而
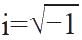的存在表明相位因子是其中另一个重要组成部分。因为非阿贝尔规范理论的作用量在规范变换下具有微妙的乘法性质，所以对称性也成为其中一个必不可少的组成部分。
令人惊讶的是，这三个主旋律均是从人类认知史中的原始概念演变而来的：量子化从测量单位的认识中发展而来；对称性概念是从认识几何形式之美的过程中发展起来的；相位概念则是从对月亮的相位进行观察的过程中形成的。20世纪的物理学赋予了这三个概念以精确的数学意义，并把它们全都集中到路径积分形式（3）中，而它所包含的丰富内容可以说是自牛顿和惠更斯以来物理学传统中最优秀的部分。
（李香莲译）