




20世纪70年代,物理学家重返场论。这次他们采用的是非阿贝尔规范理论(non-abelian gauge theory),它是麦克斯韦理论的一个优美推广。这里的形容词“非阿贝尔”有着精确含义:相继的两次操作(例如转动)得到的最终结果依赖于操作次序。 [2] 今天,在深入理解自然界中的各种相互作用的结构这个问题上,规范理论是一个基础性的概念。它起源于数学家赫尔曼·外尔(Hermann Weyl)发表于1918—1919年间的三篇文章。这些文章曾受爱因斯坦电磁学几何化的想法的影响。 [3]
外尔意识到“平行移动”这个概念的重要性。他论证道:“为了与自然界相符,黎曼几何必须建立在矢量的无穷小平行移动这一观念上。”外尔进一步说,既然在平行移动中矢量场的方向不断改变,那为什么不允许它的长度也改变呢?由此出发,外尔提出了所谓“不可积伸缩因子”(nonintegrable Streckenfacktor)的概念,或者叫Proportionalitätsfacktor,它通过如下公式和电磁场发生联系:
exp(—∫ eA μ d x μ / γ ), (5)
在这里 A μ 是四维矢量势,系数 γ 是实数。外尔给在时空中运动的每个带电物体都附加一个伸缩因子。在外尔的第二篇文章后,爱因斯坦添加了一个附注,其中爱因斯坦批评了平行移动改变长度的想法,外尔未能有力地反驳爱因斯坦的毁灭性评论。
在量子力学建立后的1925—1926年,福克(Vladimir Fock)和伦敦(Fritz London)独立指出,在量子力学里,( p — eA )应该由如下公式取代:
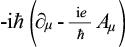 ,(6)
,(6)
这个公式又意味着在方程(5)中, eA μ d x μ / γ 应该由i eA μ d x μ / ħ 替代,也即 γ 由—i ħ 替代。
外尔显然接受了 γ 必须为虚数的想法,所以他在1929年的一篇重要文章中定义了QED 中的规范变换这一概念,并证明了麦克斯韦理论在量子力学的框架下具有规范不变性。
在任一规范变换下,外尔的长度伸缩因子应由如下因子替代:
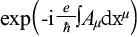 ,(7)
,(7)
它显然应该称为“相位变化因子”。通过这一替换,爱因斯坦最初的批评不再成立了。
麦克斯韦方程组具有高度的对称性,这个事实在1905—1907年间已经由爱因斯坦和闵可夫斯基(Hermann Minkowski)分别认识到,他们发现了麦克斯韦方程组的洛伦兹不变性。外尔在1929年发现了规范对称性,从而揭示了麦克斯韦方程组的又一对称性。今天我们已经知道,这些对称性使得麦克斯韦方程组成为理解物理宇宙的结构的基础支柱。
外尔的规范变换涉及时空中的逐点 U (1)转动,或者说复平面上的转动。这一点和麦克斯韦的转动涡旋有着显著相似。当然,这种相似是个巧合。
从数学上看,公式(7)中的相位因子形成一个李群 U (1),而外尔最喜爱的研究领域之一正是李群。对背景知识较多的读者,我可以提出一个猜测:假如纤维丛理论在1929年前就建立了,外尔显然会认识到电磁学就是一个 U (1)纤维丛理论,并且很有可能在那时就把它推广为非阿贝尔规范理论,因为这正是他1929年的理论的自然延伸。
历史上,这一延伸发生于1954年,并且来自不同的动机。新的动机并不是基于纯数学上的考虑。当时粒子物理实验中涌现出越来越多的“奇异粒子”,因此迫切需要一个原理来描述它们之间的相互作用。这一物理动机简洁地体现在以下这个发表于1954年的摘要里:
电荷是电磁场的源;这里有一个名为规范不变性的重要观念,它与以下几件事物有紧密联系:(1)电磁场的运动方程;(2)流密度的存在性;(3)带电场和电磁场之间的可能的相互作用。我们尝试推广这一概念,将它用于同位旋守恒。 [4]
这一推广带来了非常美妙的非阿贝尔规范场论(non-abelian field theory)。然而,这一理论似乎要求存在无质量的带电粒子,这些粒子在自然界中并没有见到,所以在很长一段时间里,这一理论在物理学界并没有得到认可。
为了给这些无质量粒子以质量,人们在20世纪60年代引进了对称性自发破缺的概念。这一概念带来了一系列重大进展,并最终带来一个基于 U (1)× SU (2)× SU (3)群的规范理论,我们今天称之为标准模型(standard model),它描述了电弱相互作用和强相互作用。从1960年左右算起,大约50年里,粒子物理领域的众多实验和理论物理学家们努力验证并发展了此标准模型,这里既有个人努力,也有集体协作。这些不懈努力获得了炫目的成功,最近的一个高潮是2012年希格斯玻色子在欧洲核子研究中心(CERN)被两个大型实验组发现(见 Physics Today ,2012年9月刊,第12页)。
尽管如此成功,标准模型也不可能是终极理论。首先,标准模型包含几十个参数。更重要的是,作为标准模型的一个核心部分,“对称性自发破缺”机制是一个纯粹唯象的构造,它在很多方面与费米的“四费米子相互作用”(four- ψ interaction)相似 [5] 。在1934年被提出后,费米理论保持了近40年的成功,但它最终被更深刻的 U (1)× SU (2) 电弱统一理论(electroweak theory)取代。
19世纪50年代汤姆孙和麦克斯韦已经明确知晓规范自由度。在难以捉摸的“电紧张态”中,法拉第可能也曾模糊地感觉到了它。1929年,外尔在量子力学的框架内把规范自由度转述为麦克斯韦方程组的一个对称性(或称“不变性”)。今天我们称这一对称性为“规范对称性”,它已经成为标准模型的结构性支柱。
麦克斯韦方程组是线性的。在非阿贝尔规范理论中,方程组是非线性的。从观念上来说,这一非线性的起源类似于广义相对论方程的非线性。关于后者,爱因斯坦曾写道:
我们在这里只讨论纯引力场的方程。
这些方程的奇特性一方面在于它们的复杂构造,特别是方程对于场变量和它们的微商的非线性特征;另一方面在于这些复杂的场定律在很大程度上几乎完全被变换群所确定。 [6]
真实的自然定律不可能是线性的,也不可能从线性方程中导出。
在完全独立于物理学发展的道路上,20世纪前半叶诞生了一个名为纤维丛(fiber bundle)的数学理论。这一理论有众多源头,包括微分形式(主要归功于嘉当[Élie Cartan])、统计学(Harold Hotelling)、拓扑学(Hassler Whitney)、整体微分几何(陈省身)以及联络理论(Charles Ehresmann)。概念起源的多样性表明了纤维丛是个核心的数学构造。
在20世纪70年代,人们发现规范理论的数学形式和纤维丛完全一致,这对物理学家和数学家都是一个震撼。 [7] 但这也是一个大家乐于感受的震撼,因为它提供了一个沟通数学和物理的桥梁,而这种沟通曾在20世纪中期前后因为数学进展的高度抽象性而中断过。
在1975年,我从我的数学同事西蒙斯(James Simons)那里学到了纤维丛理论的一些基础知识,随后我给他看了狄拉克在1931年发表的一篇关于磁单极子的文章。他惊呼:“狄拉克领先于数学家发现了平凡和非平凡的纤维丛。”
在即将结束我们这个关于规范理论观念起源的简略概述时,也许我们可以引用1867年麦克斯韦在法拉第去世的时候的悼词:
法拉第通过他的力线概念来统一地理解各种电磁感应现象,他运用这种想法的方式显示出他是一位高超的数学家——未来的数学家将能从他那里获得丰富而有价值的方法……
从欧几里得的直线到法拉第的力线,这正是推动科学进步的思想的特征。通过自由运用动力学和几何学的思想,我们也期望未来能有新的进展……
以我们正在积累的素材为基础,也许下一个像法拉第一样的哲人能够发展出全新的科学,而我们今天很可能连它的名称都还不知道。
(汪忠译)
[1] Larmor J., Proc. Cambridge Philos. Soc. ,1936,32:695. p.697.
[2] 我在《爱因斯坦对理论物理的影响》中曾介绍过规范理论,见 Physics Today ,1980年6月刊,第42页。更技术性的介绍可见于 Physics Today ,1982年3月刊,第41页,作者为辛格(Isidore Singer)。
[3] 关于这件事及其后续历史,参见杨振宁发表于下面书中的文章:Chandrasekharan K.(ed.), HermannWeyl , 1885—1985 : Centenary Lectures ,Springer,1986,p.7;以及文章:Wu A. C. T.,Yang C. N., Int. J. Mod. Phys. A ,2006,21:3235。
[4] Yang C. N.,Mills R., Phys. Rev .,1954,95:631.
[5] 费米原始论文的英文翻译见于:Wilson F. L. Am. J. Phys. ,1968,36:1150.
[6] Schilpp P. A.(ed.), Albert Einstein : Philosopher-Scientist ,Open Court,1949,p.75、89.这两段话摘自爱因斯坦在1946年(当时他67岁)的自述。
[7] Wu T. T.,Yang C. N., Phys. Rev. D ,1975,12:3845.