Set theory [1] is the theory that studies the general properties of sets,especially infinite sets.It was founded by the outstanding German mathematician George Cantor(1845—1918)in the 19th century.Since its inception,the theory has outspreaded into many branches of mathematics and becomes the basis of modern mathematics.Almost every field of mathematics can be built on the foundation of set theory.Any mathematical concept can be defined from the concept of set theory,and any mathematical theorem can be derived from the theorem of set theory.Most branches of mathematics can be unified in the framework of set theory.For example,geometry aims to study the set of points;Groups,rings and fields in abstract algebra are all sets that define some special operations;In mathematical analysis,real numbers and rational numbers are all sets,and functions are no more than synonyms of mappings between sets,and the definition domain and value domain of functions are also sets.In addition,real variable functions,functional analysis and so on all deal with various sets.
A mathematical system must start with some concepts that cannot be defined or do not need to be defined.Set is such a primitive concept which should not be defined but could be described. A set is a well-defined collection of objects .This is an intuitive description to set.The objects consisting of a set are also called elements .Let S and e denote a set and an element,respectively.If e is one of the elements of S ,it is said e is in S or S contains e and denotes this fact by e ∈ S ;If e is not one of the elements of S ,it is said e is not in S and denotes this fact by e ∉ S .A set is well-defined,meaning that the elements constituting the set must be clearly distinguishable from each other.More precisely,if S is a set and e is an element,then either e ∈ S or e ∉ S ,with no other possibilities.According to the property of well-defined,lower grade of students in a school could not be defined as a set,because “lower grade” is a vague description.The students with the weight ≥ 50kg in a class can be defined as a set,because the condition “weight ≥ 50kg” is clear enough to judge whether a student is in the set or not.
In the set theory,capital letters such as A , B , C , D are always be used to represent a set,and lowercase letters such as a , b , c or x , y , z always represent elements.Commonly used sets include:N denotes the set of natural numbers.R denotes the set of real number.Q denotes the set of rational number.More examples are given below.
S 1 :All students in a class.
S 2 :{0,1}.This set is the fundamental of logic algebra,digital circuit,and digital communications.
S 3 :All possible results of rolling two dice successively.
S 4 :In shooting practice,assuming that miss will not occur,the hit point will form a set.
S 5 :All real numbers within the interval of( a , b ).
For above examples,the elements of S 1 is every students;The elements of S 3 are a number of 36 ordered number pairs,including(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).For every element,the first number represents the point of the first dice,and the second number represents the point of the second dice.
There are two ways to describe a set.
1.Enumeration
List all elements in the set,separated by commas,and then surrounded by curly braces.Such as{ a , b , c , d }and{0,1,2,…}.It should be noted that there is no sequence for the elements within a set,so{ a , b , c , d }and{ d , c , b , a }are the identical set.
2.Description
Describe a set by the common property of elements.For example, A ={ x | x is a student in the third grade},or B ={ y | y is a natural number}.
Some concepts relative to set are given below.
Empty set :A set with no elements is called empty set,denoted by φ .The number of elements for an empty set equals zero. φ in set theory plays the role of 0 in algebra.
Subset: Set A is a subset of set B ,denoted by A ⊆ B ,if every element of A is in B .It is called A is included in B or B includes A .If A ⊆ B and there are some elements in B but not in A ,i.e.,∃ x ∈ B and x ∉ A ,then calls A is a proper subset of B ,denoted by A ⊂ B .Otherwise,calls A is an improper subset of B .According to this definition,for any set A , A is the improper subset of A .Any other subset of A is a proper subset.
According to the definition of subset,for any set A , A itself and φ are both subsets of A .Moreover,if A ⊆ B and B ⊆ A ,then calls A and B are identical.This method is always used to prove the identity of two sets.
Universal set :When discussing a specific problem,ones need to select a “largest” set,which contains all elements related to the problem,so that all other sets become its subsets.Such the “largest” set is called universal set or complete set,denoted by Ω .
Set class :A set with sets as its elements is called a set class,i.e.,a set class is a “set of set”.
Set function :A set function is a function with sets as variable.Thus,the definition domain of a set function should be a set class.
The operation of sets means operations between sets,which includes intersection,union,difference,complement,Cartesian product,and power set.The operation result of sets is a new set.Set theory always use Voronoi diagram to depict the operations of sets.In a Voronoi diagram,the biggest rectangle represents the universal set Ω ,some smaller regions within Ω represent subsets.
1.Intersection( A ∩ B )
The intersection of sets A and B ,denoted by A ∩ B ,is a set whose elements are in both A and B ,i.e., A ∩ B consists of the common elements of A and B .With the description method,
A ∩ B ={ x | x ∈ A and x ∈ B }
A ∩ B could also be briefly denoted as AB .If there is no intersection of A and B ,i.e., A ∩ B = φ ,it is said A and B are disjoint or mutually exclusive.This property could be generalized to three or more sets.The sets A , B ,and C are mutually exclusive if and only if they are mutually exclusive in pair,i.e.,
A ∩ B ∩ C = φ , A ∩ B = φ , A ∩ C = φ and B ∩ C = φ
Thus,ones could not say A , B ,and C are mutually exclusive if only A ∩ B ∩ C = φ is satisfied.Please see Figure 1.1.1 for illustration.
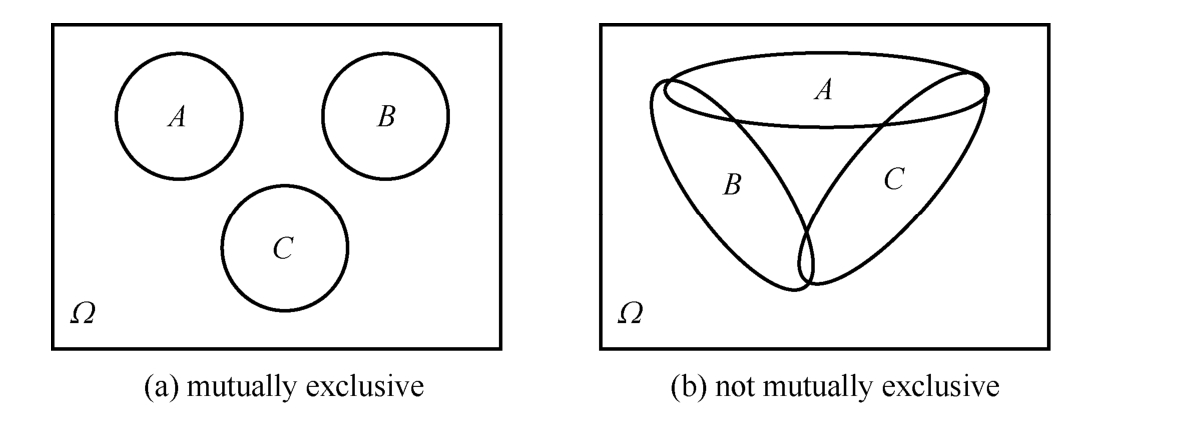
Figure 1.1.1 Illustration of mutually exclusive
2.Union( A ∪ B )
The union of two sets A and B ,denoted as A ∪ B ,is a set whose elements are either in A or in B ,i.e., A ∪ B consists of all elements of A and B .With the description method,
A ∪ B ={ x | x ∈ A or x ∈ B }
If A and B are disjoint, A ∪ B could also be written as A + B .
Specially,if A ∩ B = φ and A ∪ B = Ω are both satisfied,it is said A and B are opposite.Such phenomenon could exist within a finite number of sets.For a sequence of sets,say A 1 , A 2 ,…, A n ,if the following property is satisfied
A
1
,
A
2
,…,
A
n
are mutually exclusive and
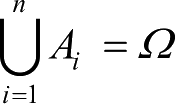
Then we say A 1 , A 2 ,…, A n are completely exclusive,or they become a partition of Ω .
3.Difference( A - B )
The difference of two sets A and B ,denoted as A - B or A \ B ,is a set whose elements are in A but not in B .With the description method,
A - B ={ x | x ∈ A and x ∉ B }
It should be noted that the operations of intersection and union are commutative,but difference is not.
4.Complement( A c )
The complement of set A ,denoted as A c or A ,is the difference set of the universal set Ω and A ,i.e., A c = Ω - A .So, A c is the set whose elements are in Ω but not in A . A c is also called the absolute complement of A .Comparatively,the difference A - B is also called the relative complement of the set B versus A .It is not difficult to prove the property of A - B= AB c .
The above mentioned four operations could be illustrated by Voronoi diagrams.See dash area in Figure 1.1.2.
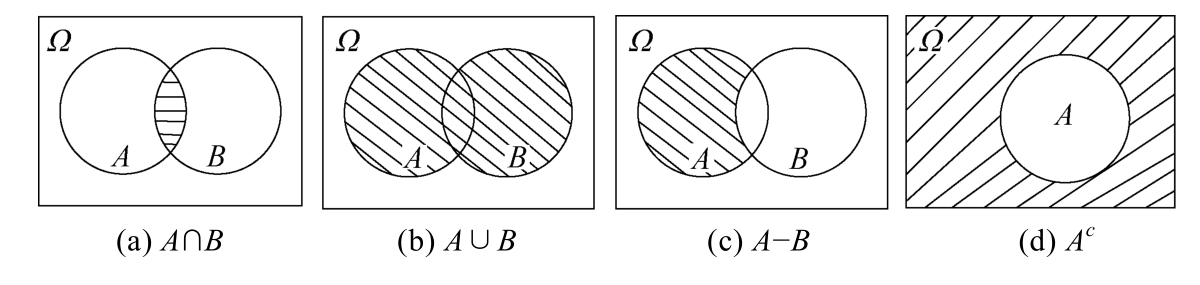
Figure 1.1.2 Four operations of sets
5.Cartesian product( A × B )
The Cartesian product of sets A and B ,denoted as A × B ,is the set of ordered pairs( x , y ),where x ∈ A and y ∈ B .With the description method,
A × B ={( x , y )| x ∈ A and y ∈ B }
Because every element( x , y )is an ordered pair, A × B ≠ B × A ,i.e.,Cartesian product is not commutative.
6.Power set(2 A )
The power set of a set A ,denoted as 2 A ,is comprised of all subset of A ,i.e.,the elements of 2 A are all subset of A .If the number of elements in A equals n ,then the number of elements in 2 A equals 2 n .
Example 1.1.1 Let Ω ={1,2,3,4,5,6,7,8,9,0}, A ={1,2,3}, B ={2,3,5}.Then,
A ∩ B ={2,3}
A ∪ B ={1,2,3,5}
A - B ={1}
A c ={4,5,6,7,8,9,0}
A × B ={(1,2),(1,3),(1,5),(2,2),(2,3),(2,5),(3,2),(3,3),(3,5)}
2 A ={ φ ,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}
The operations of sets have the following properties.
1.Commutative la w
A ∪ B = B ∪ A
A ∩ B = B ∩ A
2.Associative law
( A ∪ B )∪ C = A ∪( B ∪ C )
( A ∩ B )∩ C = A ∩( B ∩ C )
3.Distributive law
( A ∪ B )∩ C =( A ∩ C )∪( B ∩ C )
( A ∩ B )∪ C =( A ∪ C )∩( B ∪ C )
4.De Morgen law
( A ∪ B ) c = A c ∩ B c
( A ∩ B ) c = A c ∪ B c
Mapping is a synonym for the notation of function.Intuitively,a function f from one set X to another set Y is a “rule”,which assigns to each element x ∈ A a unique element y = f ( x )∈ B .This is written as
f : X → Y
It is said that f is a mapping defined on X and taking values from Y . X is called the definition domain of f .ran( f )={ y | y = f ( x ), x ∈ X }is called the value domain of f . x and y are called the primitive image and image of f ,respectively.
Specially,a mapping f : X → Y is called an injection (or one-to-one)if f ( x )= f ( x' )implies x = x' ;If Y = ran( f ),i.e.,every element y in Y has its primitive image x ,the mapping f is called a surjection (or onto);A mapping is called a bijection if it is both an injection and a surjection.See Figure 1.1.3 for illustration.
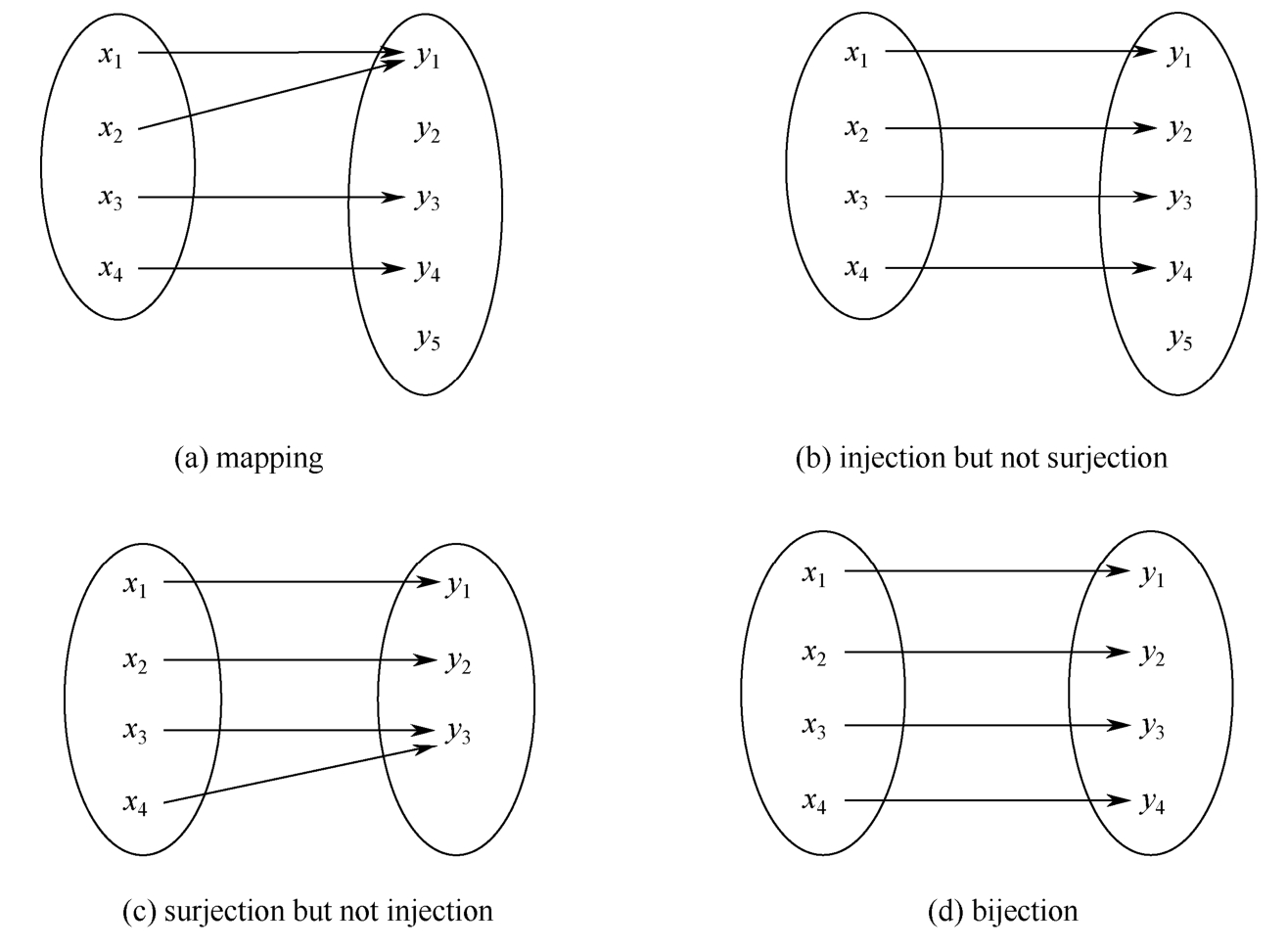
Figure 1.1.3 Four types of mappings
If a bijection f : X → Y exists,it is called X and Y are equivalent,denoted by X ~ Y .It should be emphasized that equivalent does not means identical.
Example 1.1.2
(1){1,2}~{0,2}.
(2) A ={1,2,3,4,5, … }~ B ={2,4,6,8,10,…}.
(3) X= [0,1]~ Y= [0,2].
(4)In Figure 1.1.4, AB ~ CD .
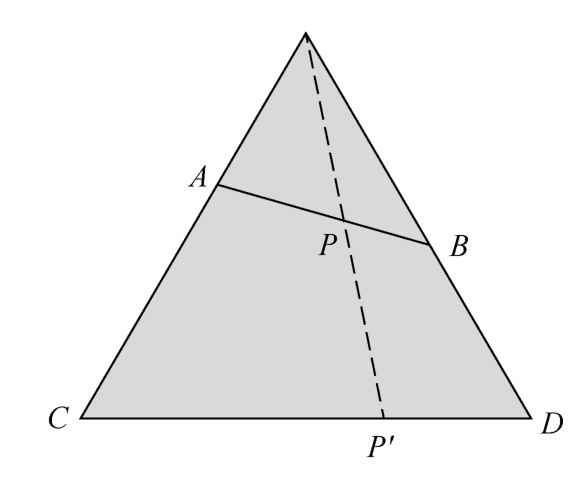
Figure 1.1.4 Two segments AB and CD are equivalent
Within four mappings in this example,(1)is trivial;(2)and(3)could be easily verified by “double” operation;In(4),for any point P on AB ,it can be mapped to a point P' on CD by the dashed line,and vice versa,so AB and CD are equivalent.
Revisiting(2)and(4)in this example,ones could find an interesting and surprising phenomenon.Equivalence could exist between a set and its proper subset.Such equivalence relationship with its proper subset cannot occur in a finite set with a finite number of elements.Only an infinite set can have such property.In fact,this property is also a definition of infinite set.
Definition 1.1.1 A set is an infinite set if it is equivalent to its proper subset.Otherwise,it is a finite set.
In history,infinity has always been a topic in philosophy.For a long time,people did not know whether there was a difference in size between infinite sets and how to distinguish the size of infinite set.Until the 1870s,the great German mathematician Cantor made an in-depth study on whether infinite sets can be compared in size.He not only introduced infinite numbers into mathematics,but also divided infinite numbers into different types,thus giving the answer to this problem and creating the set theory that has become the basis of various disciplines of modern mathematics.
The number of elements in a set is a natural description of the size of a set.For a finite set,the number of elements can be counted,although it is boring.But for an infinite set,the number of elements is infinite,how can we compare the size? Based on the concept of equivalence,Cantor proposed that the sizes of two infinite sets are identical if the two sets are equivalent.Further,call the common size the cardinality of the two infinite sets.It is stipulated the cardinality of empty set is zero.Obviously,the cardinality of a finite set should be a natural number.The cardinality of an infinite set is generally called a transfinite number.
The charm of set theory is shown in infinite sets.The first familiar infinite set is the set of natural numbers N={0,1,2,3,4,…}.The cardinality of natural number set is denoted by
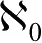 .
.
Definition 1.1.2 A set is a countable set if it is equivalent to the natural number set N.Any infinite set other than countable set is uncountable set.
This definition implies that all countable sets are equivalent with the common cardinality of
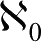 .
.
Example 1.1.3 The following sets are all countable sets.
(1){1,2,3,4,…};
(2){2,4,6,8,…};
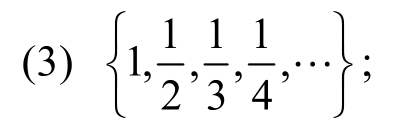
(4){…,-3,-2,-1,0,1,2,3,…}.
Countable sets have the following properties.
(1)The union set of a finite number of countable sets is a countable set.
(2)The union set of a countable number of countable sets is a countable set.
(3)If A and B are two countable sets,then A × B is a countable set.
Theorem 1.1.1 The set of rational numbers Q is a countable set.
Proof:Q = Q + ∪{0}∪Q - ,where Q + and Q - represent positive and minus rational numbers,respectively.Take Q + as an example,
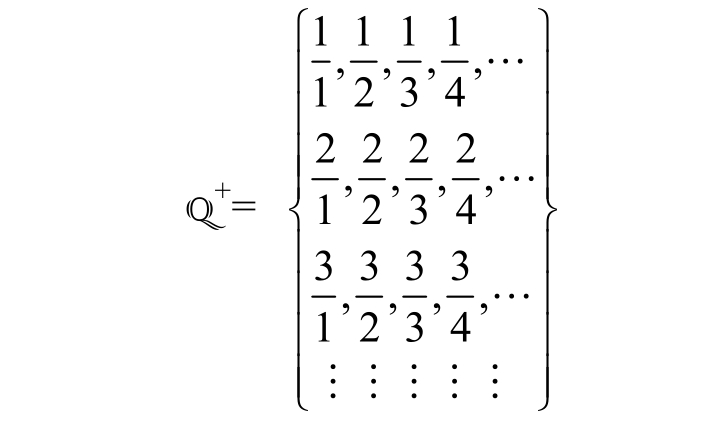
It could be seen every row in Q + is a countable set and the number of rows is countable.That is to say,Q + is the union set of a countable number of countable sets,so according to the property(2),Q + is a countable set.Similarly,Q - is a countable set.Then,Q = Q + ∪{0}∪Q - is the union set of a finite number of countable sets,which implies Q is a countable set according to the property(1).It is a conclusion that is drastically contrast to the intuition.The number of rational numbers seems to be much more than that of natural numbers N,but the cardinality of the two sets is actually equal.
Another interesting property of the rational number set is density ,that is,no matter how short the interval is on the axis,as long as the interval length is not zero,there are always infinitely many rational numbers in it.See Figure1.1.5 as an example.Rational number and real number are dense sets.In comparison,natural number and integral number are sparse sets.
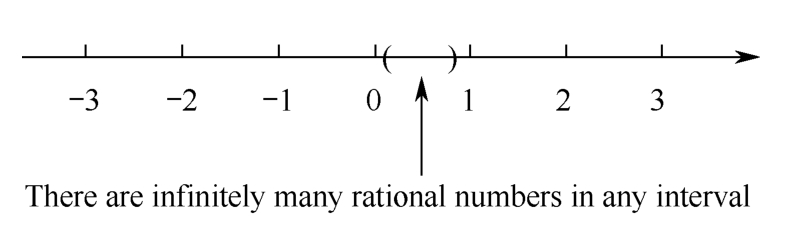
Figure 1.1.5 A dense set
Theorem 1.1.2 The set of real numbers R is an uncountable set.
The cardinality of R is another transfinite number,which is denoted by
c
.Based on the continuum hypothesis,there is 2
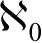 =
c
and there is no type of set whose cardinality is between
=
c
and there is no type of set whose cardinality is between
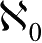 and
c
.
and
c
.
It seems that the set of real number is very large.Is there an infinite set whose cardinality is greater than c ? The answer is yes.If the cardinality of a finite set A is a ,it is easy to verify that the cardinality of the power set 2 A equals 2 a ,which is greater than a .Please check Example 1.1.1.A similar conclusion is also true for infinite sets.The cardinality of the power set of the real number set is 2 c > c .If the operation of the power set continues,its cardinality will continue to grow.So it gets the conclusion that there is no the largest cardinality.
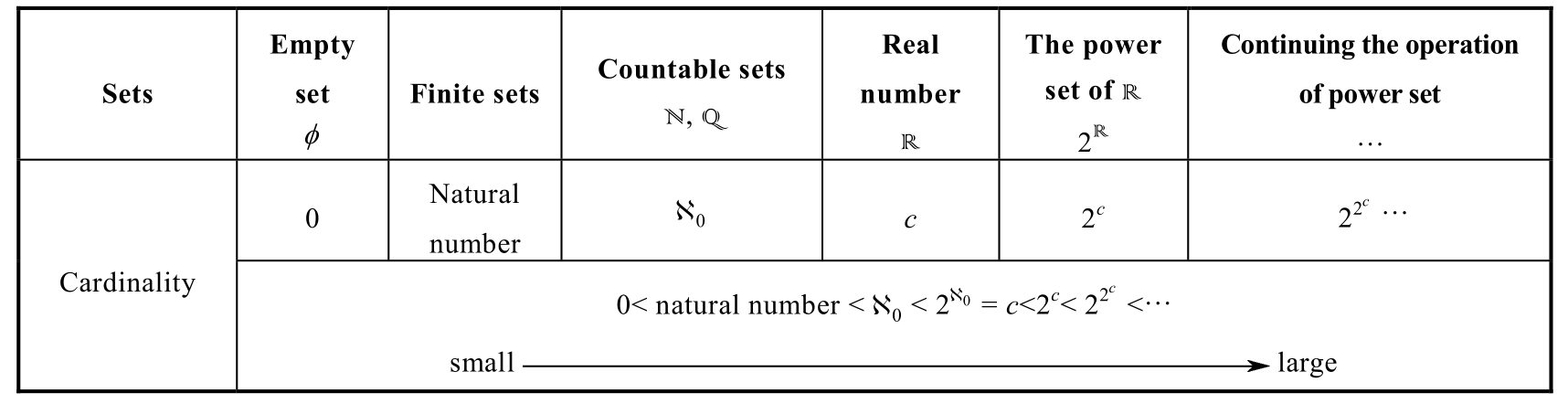
According to the discussion above,sets can be classified according to cardinality.The sets can be divided into finite sets and infinite sets,and infinite sets can be divided into countable sets and uncountable sets,As Figure 1.1.6 shows.In engineering applications,the terms discrete sets and continuous sets are often used.The discrete set includes finite set and countable set,and the continuous set refers to uncountable set.Table 1.1.1 shows the comparison of cardinality of various sets,which verifies the fact that there is no biggest cardinality.
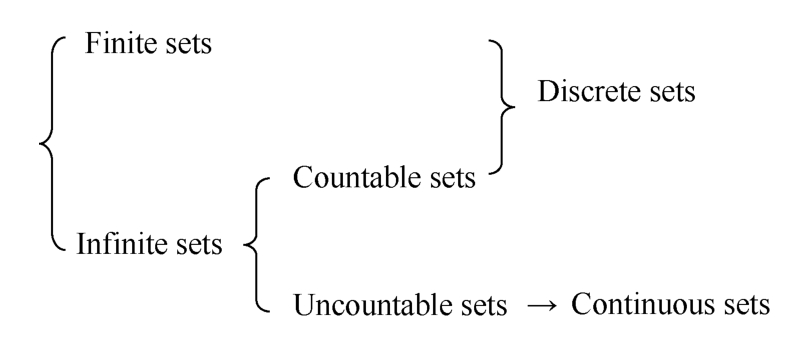
Figure 1.1.6 The classification of sets
Table 1.1.1 The comparison of cardinality of various sets