




快衰落也称为小尺度衰落,是由多径信号相干叠加引起的,描述的是信号在短期范围内的衰落。具体来说,是指当移动设备移动一个较小的距离时,接收信号在短期内的快速波动情况。影响快衰落的因素主要包括多径效应、多普勒效应、信号的传输带宽等。在无线通信系统中,接收信号往往是多径信号的叠加,多径信号的幅度、相位等参数具有随机性,多径效应就是由收发两端之间的多条信号传播路径的相长干扰和相消干扰造成的信号失真和错误。移动台在高速移动的情况下或者所处的多径环境处于快速变化时,都会产生多普勒效应,即接收信号的频率会由于收发两端的相对运动而发生变化。当信号的传输带宽大于多径信道的相干带宽时,接收信号就会出现失真。
快衰落模型主要需要考虑时间色散参数、频率色散参数及空间色散参数。在地面通信系统中常用瑞利衰落表示小尺度衰落,无人机通信网络与地面通信系统不同,由于无人机通信网络具有LoS链路传播的特征,莱斯衰落模型或者Nakagami -m 衰落模型更适合无人机对地的通信。
当信号中存在视距传播的成分时,接收信号的均值是非零的,是直射成分和复高斯信号的叠加。在这种情况下,可用莱斯分布对信号包络建模,即:
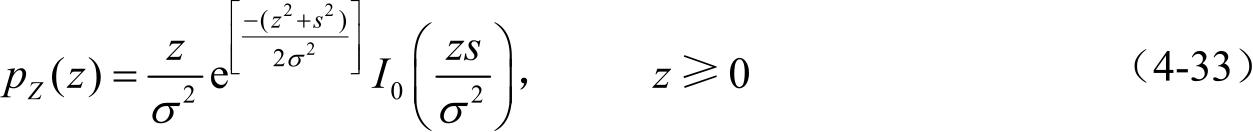
接收信号的平均功率为:

莱斯分布也常用衰落参数 K = s 2 /(2 σ 2 )来表示,此时式(4-33)可写成:
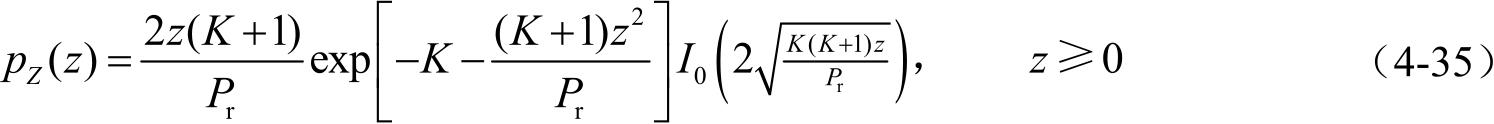
Nakagami -m 衰落模型是为了解决瑞利分布和莱斯分布在应用中偶尔存在的与实验数据不够符合的问题。Nakagami -m 衰落模型的应用场景与莱斯模型相似,但也能对瑞利衰落这样糟糕的衰落进行建模。Nakagami -m 的分布式表示为:

式中, P r 为接收信号的平均功率; Γ ( m )为伽马函数; m 为衰落参数。改变 m 的值,Nakagami -m 衰落可以转变为多种衰落。当 m =1时,Nakagami -m 衰落可退化为瑞利衰落;当 m =( K +1) 2 /(2 K +1)时,Nakagami -m 衰落可近似为衰落参数为 K 的莱斯衰落;当 m =∞时表示无衰落。
时间色散参数是用平均附加时延、时延扩展和最大附加时延扩展等参数来描述的,这些参数是由功率时延分布来定义的。最大附加时延表示最晚到达的多径成分的到达时间,在实际中最晚到达的信号功率可能比噪声功率还小,因此常常不考所谓最晚到达时延,而是考虑多径能量低至某一门限时的最大时延。设置门限的目的是对噪声和多径成分加以区分,其值过低会将噪声误认为多径成分,而过高则会遗漏某些多径成分。门限取值会对时间色散参数的值造成影响。平均附加时延是所有多径成分到达的平均时延,计算公式为:
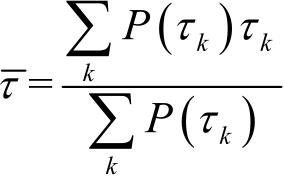
式中,
P
(
τ
k
)是路径
k
的到达功率;
τ
k
是路径
k
的时延。均方根时延扩展是所有到达的多径成分附加时延的标准差,其表达式为
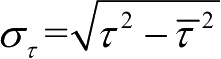 。
。
频率色散参数是用多普勒扩展来描述的,而相关时间是与多普勒扩展相对应的参数。与时延扩展和相关带宽不同的是,多普勒扩展和相关时间描述的是信道的时变特性。这种时变特性是由移动台与基站间的相对运动或者信道中的物体运动引起的。
在无人机通信网络中需要综合考虑三维空间内的信道空间特性。三维信道建模的一个重点是如何将水平维度信道的二维信道扩展为同时包括水平维度信道和垂直维度信道的三维信道,因此需要增加模型的水平角度分布和垂直角度分布。
水平角度和垂直角度的定义如图4-3所示,假设水平面为
xOy
平面,垂直方向为z轴方向,则水平角度可定义为空间多径方向在
xOy
平面上的投影与
x
轴正方向的夹角,垂直角度可定义为空间多径方向与坐标系
z
轴正方向的夹角。在图4-3中,若
 为空间多径的方向,则对应的水平角度为
ф
,垂直角度为
θ
。
为空间多径的方向,则对应的水平角度为
ф
,垂直角度为
θ
。
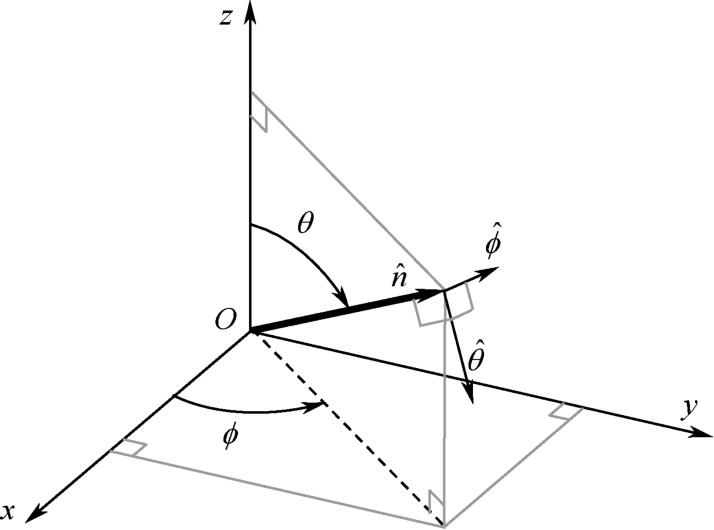
图4-3 水平角度和垂直角度的定义
在三维信道模型中,一条路径对应4个角度,包括水平发射角、水平到达角、垂直发射角、垂直到达角,具体定义如下:
➲水平发射角(Azimuth of Departure, AOD):空间信道多径与发送端水平方向的夹角。
➲水平到达角(Azimuth of Arrival, AOA):空间信道多径与接收端水平方向的夹角。
➲垂直发射角(Zenith of Departure, ZOD):空间信道多径与发送端垂直方向的夹角。
➲垂直到达角(Zenith of Arrival, ZOA):空间信道多径与接收端垂直方向的夹角。
除了可以使用ZOD、ZOA定义垂直角度,还可以使用EOD(Elevation of Departure)/EOA(Elevation of Arrival)定义垂直角度。这两种定义的区别在于参考坐标的不同,ZOD/ZOA表示 z 轴正方向到多径方向的夹角,而EOD/EOA表示水平面到多径方向的夹角。
在采用基于几何的随机信道建模方法(Geometry Based Stochastic Modeling, GBSM)对三维信道进行建模的过程中,需要利用射线跟踪的方法对仿真场景内的所有散射多径成分的特性进行统计建模,从而计算出信道的冲激响应。用于描述多径成分的统计特性的参数包括时延扩展参数、LoS增益参数、阴影衰落参数和角度扩展参数。多径成分统计互相关矩阵是由以上每两个参数互相关系数所组成的矩阵,若描述信道的多径成分需 N 个参数,则多径成分统计互相关矩阵为 N × N 的对称正定矩阵。多径成分统计互相关矩阵具有以下性质:
➲多径成分统计互相关矩阵是正定矩阵;
➲多径成分统计互相关矩阵的对角线上元素为1。
在二维信道建模中,角度扩展参数仅包括水平维两个扩展参数——ASD(Azimuth Spread of Departure Angle)和ASA(Azimuth Spread of Arrival Angle),即二维信道中共有5个参数(DS、ASD、ASA、 K 、SF),多径成分统计互相关矩阵为5×5的正定矩阵,如式(4-37)所示。

由于三维信道对垂直角度进行建模,所以信道的角度扩展参数除了水平角度扩展参数,还应包括垂直角度ZOD/ZOA的角度扩展参数ZSD/ZSA,即三维信道需7个参数(DS、ASD、ASA、 K 、SF、ZSD、ZSA)来描述多径成分的统计特性。多径成分统计互相关矩阵为7×7的正定对称矩阵,如式(4-38)所示。
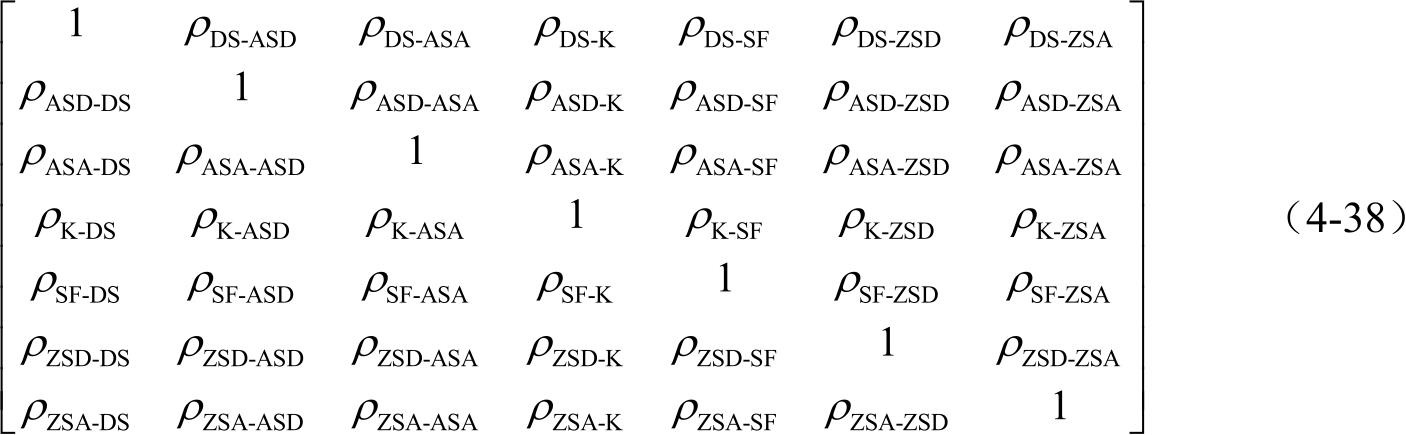
矩阵中7个参数的顺序是不固定的,可以是任意顺序;矩阵中 ρ DS-ZSD 和 ρ ZSD-DS 的意义相同,均表示参数DS与ZSD的互相关系数,其他参数意义以此类推;矩阵中对角线上的1表示同一个参数的自相关系数为1。
三维信道的多径成分统计互相关矩阵是在WINNER信道模型和信道模型二维信道互相关矩阵的基础上扩展得到的。对于式(4-38)中数互相关系的定义,根据实测数据以及射线跟踪的仿真结果,出现了不同的互相关矩阵方案。由于互相关矩阵由实测数据经过统计得到,没有理论依据可以判断哪个方案更接近实际三维信道。在4.4节中,我们将介绍3GPP关于三维无人机信道建模的模型和参数确定方法。
垂直发射角角度扩展是垂直发射角的角度扩展,垂直到达角角度扩展是垂直到达角的角度扩展。多径成分的角度扩展参数是一个随机分布参数,服从指数正态分布,即三维信道模型中需要定义ZSD、ZSA两个随机量的均值和方差。与其他多径成分统计参数的定义方式相同,垂直角度扩展ZSD、ZSA随机分布参数的定义是由信道实测数据统计得出的。首先,由于三维信道中水平角度扩展ASD、ASA的分布参数直接沿用了二维信道的定义,因此需要考虑垂直角度扩展是否能借鉴水平角度扩展的方法,将ZSD、ZSA的均值和方差定义为常数。其次,由于三维信道中收发两端分布在不同的高度上,还需要考虑角度扩展参数与无人机高度以及距离的相关性。对于ZSD的定义,由于楼层高度相对固定,即每个楼层与发送端的垂直方向相对角度相对固定,所以三维信道中ZSD的分布参数(均值/方差)具有高度相关性和距离相关性,此结论与实测数据趋势吻合。对于ZSA的定义,由于城市中存在较多的建筑物,多径信号经过折射、散射等后,到达角是随机分布的,与无人机的高度无关。经实测数据验证,三维信道中ZSA的分布参数(均值/方差)为固定值,与无人机高度和距离没有相关性。
ZOD和ZOA分别表示UE和基站之间多径的垂直发射角和到达角。借鉴二维信道AOD、AOA的生成方法,结合实测数据可以得出ZOD、ZOA的生成方法。
(1)步骤1:确定垂直角度扩展ZOD、ZOA的统计特性。由于用户在垂直方向与水平方向的分布不同,所以垂直角度扩展的统计特性不能沿用二维信道中水平角度扩展的统计特性,需要通过分析实测数据得到。根据射线跟踪仿真结果可知,ZOD、ZOA的角度服从拉普拉斯分布。以ZOA为例(ZOD计算方法与ZOA相同),与功率相关的垂直角度分布计算为:
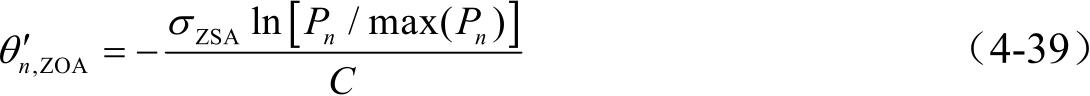
式中, P n 为多径信号的功率; σ ZSA 为角度扩展的均方根; C 为与多径数量相关的比例因子。垂直角度的比例因子 C 由实测数据分析得到,当簇数(Clusters)等于12、19、20时,比例因子取值如表4-2所示;当簇数不等于12、19、20时,垂直角度的 C 与水平角度的 C 相同。
表4-2 比例因子取值

若传播路径中存在LoS链路,则需要用 C LoS 代替 C 计算垂直角度扩展。
C LoS = C (1.3086+0.0339 K -0.0077 K 2 +0.0002 K 3 )
式中, K 为LoS链路的莱斯因子。
(2)步骤2:随机化垂直角度扩展ZOD、ZOA。ZOD、ZOA的随机化过程沿用了二维信道中水平角度的随机化过程。以ZOA为例,首先通过乘以符号量
X
n
∈{1,-1}来随机化角度的正负号,在此基础上叠加一个随机数
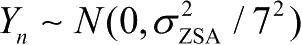 引入随机性,最后与LoS链路的垂直到达角
引入随机性,最后与LoS链路的垂直到达角
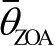 相加,即可得到传播路径的随机化垂直到达角
θ
n
,ZOA
。ZOA的随机化为:
相加,即可得到传播路径的随机化垂直到达角
θ
n
,ZOA
。ZOA的随机化为:

ZOD的随机化过程为:

通过观察可知,ZOD与ZOA的区别在于ZOD除了引入LoS链路垂直角度,还叠加了 μ offset,ZOD 。这是由于分析实测数据得到ZOD的角度随无人机高度和距离的变化而变化,所以在生成随机化的ZOD时需要添加 μ offset,ZOD 并引入UE高度相关性及距离相关性。
(3)步骤3:计算每条路径的所有子径ZOD、ZOA。在三维信道模型中,每条路径包括多条子径,需要计算每条子径的ZOD、ZOA参数。在每条路径的ZOD、ZOA上添加子径参数过程为:在每条路径的垂直角度上添加子径偏移,生成每条子径的垂直角度;由于垂直角度被定义为与 z 轴正方向的夹角,夹角取值范围为[0,180°],所以需要将每条子径的垂直角度映射到这个范围内。
①生成每条子径垂直角度的过程如下,ZOD与ZOA的生成子径角度的过程不同,需要分开讨论:
(a)生成第 n 条路径中第 m 条子径的ZOA,如式(4-42)所示。

式中, C ZOA 为每条路径内子径偏移的均方根,由实测数据统计得到; α m 为每条子径的偏移量, α m 沿用水平角度的相应定义。
(b)生成第 n 条路径中第 m 条子径的ZOD,如式(4-43)所示。
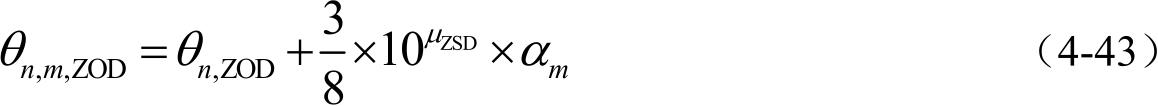
式中, μ ZSD 为ZSD指数正态分布的均值, α m 与ZOA相同。
②计算每条子径的ZOD、ZOA后,需要将每条子径的ZOD、ZOA映射到[0,180°],垂直角度映射过程如下(ZOD与ZOA的映射过程相同):
(a)通过取模运算将ZOD、ZOA映射到[0,360°]。
(b)若ZOD、ZOA在[0,180°]范围内,则不做运算;若 θ n , m ,ZOA/ZOD ∈[180°,360°],则使用(360° -θ n , m ,ZOA/ZOD )将ZOD、ZOA映射到[0,180°]范围内。
通过以上3个步骤可以生成三维信道中每条路径的每条子径的垂直角度ZOD、ZOA。每条子径的垂直角度与无人机位置和大尺度分布有关,会影响到小尺度衰落和信道的生成。