




大尺度衰落用于表示收发两端的长距离或长时间范围内的场强变化情况,包括路径损耗和阴影衰落两种类型。路径损耗是指收发两端之间的由传播环境引入的衰减,满足幂函数定律,即信号的衰减程度与距离的平方成反比。阴影衰落是指电波在传播时受到山体、建筑等固定障碍物的阻挡而形成的电波阴影区,阴影区中信号场强较弱。当移动台进入阴影区时就会出现阴影效应,阴影衰落服从对数正态分布。
在非频率选择性信道上的通用无线信道模型中,收发两端之间的复信道系数可以表示为:

式中,
β
(
d
)表示大尺度衰落,包括路径损耗和阴影衰落;
d
表示收发两端之间的距离;
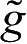 表示由于多径传播或多普勒频移带来的小尺度衰落,它通常是一个复数随机变量,其值满足
表示由于多径传播或多普勒频移带来的小尺度衰落,它通常是一个复数随机变量,其值满足
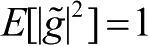 。
。
路径损耗的经典模型是对数距离路径损耗模型,这是一个3GPP和ITU都推荐使用的标准信道模型,其表达式为:

式中,
α
是路径损耗指数,通常取值为2~6之间,由该区域中建筑或植被的密度、种类、高度等因素决定。当
α
=2时表示传播环境是自由空间,空间中的障碍物越多,
α
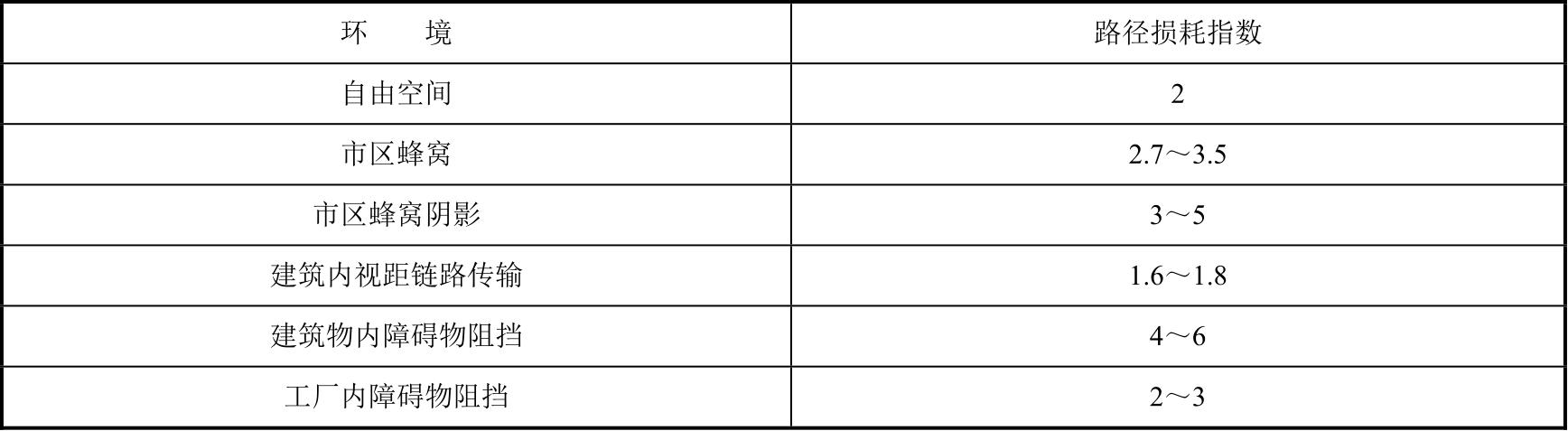
的值越大,其取值如表4-1所示。
X
0
表示距离为1m时的路径损耗,其数值取决于工作频段和天线增益等因素。
X
σ
~
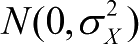 表示阴影衰落,表示均值为0、方差为
表示阴影衰落,表示均值为0、方差为
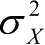 的正态(高斯)随机变量。式(4-2)表明相同位置的接收机受到随机阴影衰落的影响而具有不同的路径损耗。
的正态(高斯)随机变量。式(4-2)表明相同位置的接收机受到随机阴影衰落的影响而具有不同的路径损耗。
表4-1 路径损耗指数的取值
与传统的地面通信系统相比,无人机通信网络工作在空中,信号传播空间具有三维特性,这就导致其大尺度衰减往往更加复杂。无人机通信网络的典型特征是收发两端之间同时存在直射链路和反射时延链路,但由于空域相对地面具有空间较为开阔的特点,直射链路的占比很大。为此,已有的研究提出了以下三类信道模型:自由空间信道模型、基于高度/角度参数的信道模型、概率LoS信道模型。
如果存在一个没有信号阻挡和反射的理想场景,我们就可以得到不存在阴影衰落和快衰落的自由空间信道传播模型。在本节中,我们令式(4-1)中的
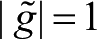 ,即不考虑快衰落,则信道功率可以表示为:
,即不考虑快衰落,则信道功率可以表示为:

式中,
λ
是载波波长;
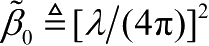 ,表示在距离为1m时的信道功率。根据自由空间路径损耗模型可知,信道功率完全由收发两端的距离决定。如果收发两端的位置已知,则可以很容易得到信道功率。自由空间信道模型在早期的无人机通信网络研究中被广泛采用。
,表示在距离为1m时的信道功率。根据自由空间路径损耗模型可知,信道功率完全由收发两端的距离决定。如果收发两端的位置已知,则可以很容易得到信道功率。自由空间信道模型在早期的无人机通信网络研究中被广泛采用。
虽然自由空间信道模型是一个理想化的模型,但仍然具有一定的应用性。我们注意到,相比于传统的地面通信信道,无人机对地通信主要是通过LoS链路实现的,因此自由空间信道模型符合无人机通信中的某些特定场景。例如,自由空间信道模型可适用于对乡村地区路径损耗的估计,因为在乡村地区,信号传播时受到的阻挡和散射较少。当无人机飞得足够高时,无人机与地面基站具有较大概率的LoS链路,因此自由空间信道模型也是适用的。但对于城市地区,建筑物的高度与无人机的飞行高度相比是不能被忽略的,此时使用自由空间信道模型就显得过于简单了。因此,当无人机的飞行高度发生变化时,需要改进信道模型使之能够反映传播环境的变化。
在城市中无人机-地面信号传播如图4-1所示。随着无人机不断爬升,信号传播受到的障碍物阻挡和散射呈现减少的趋势。为了清楚地描述这个特点,人们在自由空间信道模型中引入了高度或角度参数。
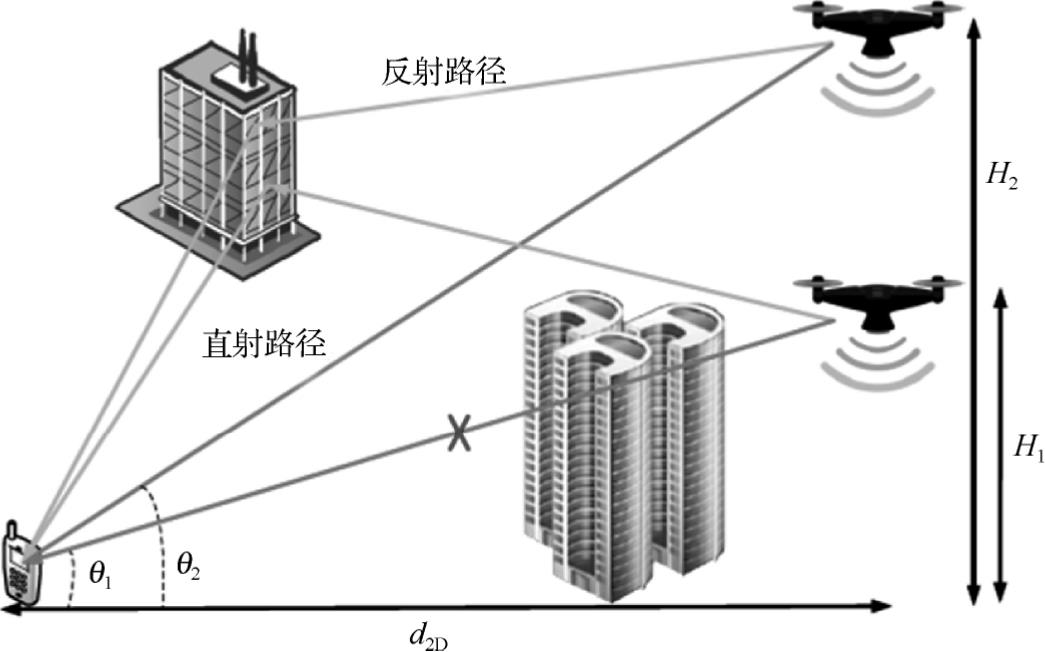
图4-1 在城市中无人机-地面信号传播
1)基于高度参数的信道模型
对于GBS-UAV链路,可以将式(4-2)中的各个变量描述为关于无人机飞行高度 H UT 的单调递减函数,即:
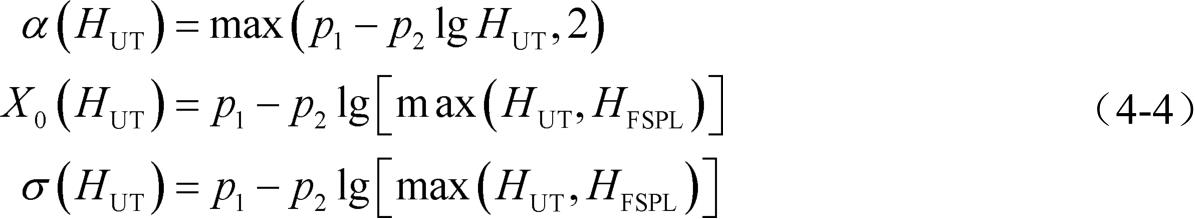
式中, p 1 ( p 1 >0)和 p 2 ( p 2 >0)是建模参数,可以通过基于信道测量结果的曲线拟合获得; H FSPL 表示信号可被视为自由空间传播时的无人机飞行高度。上述模型精确反映了当无人机向高处移动时信号受到的阻挡和散射通常会更少的特点,路径损耗指数、阴影衰落等均呈现递减的趋势。当 H UT 足够大时,就可得到 α =2的自由空间传播模型。注意,尽管上述模型是针对GBS-UAV链路提出的,但其在理论上同样适用于UAV-GT链路(注意:使用的参数不同)。由于地面基站常常是被架高的,因此GBS-UAV链路通常会比UAV-GT链路受到较少的障碍物阻挡。
2)基于角度参数的信道模型
尽管基于高度参数的信道模型能够反映无人机飞行高度变化对通信环境的影响,但在实际应用中,相同飞行高度的通信环境也是有所差别的。当无人机向靠近/远离地面基站的方向飞行时,信号的传播环境就会发生改变。为了解决这个问题,将信号的传播环境建模为有关仰角 θ 的函数(如图4-1所示),函数的值取决于无人机的飞行高度和无人机与地面基站的相对水平距离。
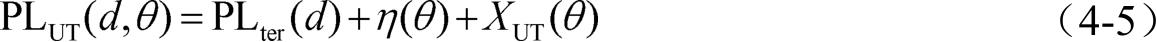
式中,PL
ter
(
d
)是地面基站和无人机下方位置间的传统地面路径损耗,可由式(4-2)计算得到;
η
(
θ
)是多余路径损耗;
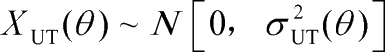 ,表示多余的阴影衰落成分。
η
(
θ
)和
,表示多余的阴影衰落成分。
η
(
θ
)和
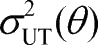 可建模为关于
θ
的函数,即:
可建模为关于
θ
的函数,即:
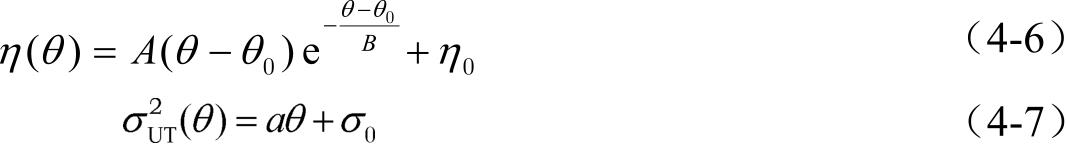
式中, A 、 B 、 θ 0 、 a 、 σ 0 是模型参数,可以基于对测量数据的曲线拟合获得, A <0,因此 η ( θ )随着 θ 的增加先减小后增大。这一方面是因为随着无人机飞行高度的增大,障碍物的阻挡和散射减少了;另一方面是因为链路距离的增加使地面基站天线增益下降了。
基于角度参数的信道模型的优点是对传播信道进行了一致性的考虑。例如,当一架无人机向一座地面基站靠近时,其通信信道将从一个部分视距传播环境逐渐转变为完全视距传播环境,这就会产生截然不同的信道特征,其路径损耗指数、阴影衰落都会发生变化。在基于角度的信道模型中,对于给定的仰角,直射路径将始终与地面通信保持一致的相互作用。
在城市中,无人机与地面基站之间的LoS链路会不时受到地面障碍物的阻挡。为了区分LoS链路和NLoS链路的不同传播环境特点,一种常用的方法是根据两种传播路径的发生概率对LoS链路和NLoS链路分别进行建模,称为概率LoS信道模型。两种传播路径的发生概率通常可以基于城市地区的统计模型得出,如该城市地区中建筑物的密度和高度等。对于给定的发射机和接收机位置,信号通过LoS链路传输的概率可通过计算在发射机和接收机的视距上没有建筑物的概率得到。针对无人机-地面通信,人们提出了不同的视距概率表达式和相应的信道模型。下面介绍基于角度参数的概率LoS信道模型。
基于角度参数的概率LoS信道模型将式(4-1)中的大尺度衰落 β ( d )建模为:

式中, β 0 是在LoS链路下距离为1m时的路径损耗; κ <1,表示由NLoS链路带来的附加衰减系数。概率LoS信道模型可使用仰角 θ 的函数来表示,即:

式中, a 和 b 是模型参数。式(4-9)表明LoS链路的概率随着仰角的增大而增大,最终趋近于1。
基于角度参数的概率LoS信道模型,在考虑周围建筑物的随机性和小尺度衰落的情况下,信道功率期望为:
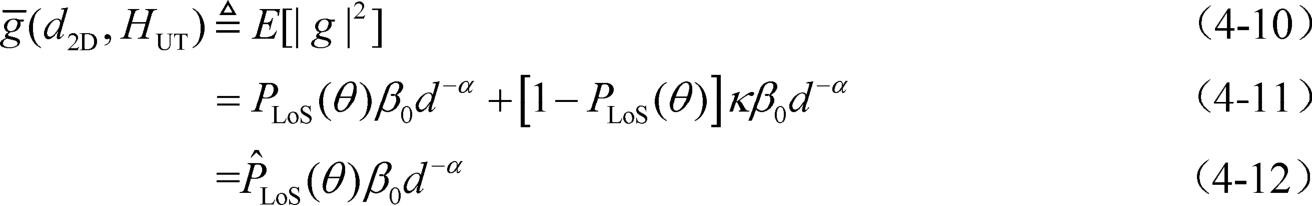
式中,
d
2D
和
H
UT
分别为地面基站到无人机的距离和无人机的飞行高度;
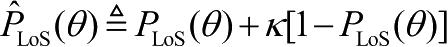 可以看成考虑了由NLoS链路造成的附加衰减因子的正则LoS概率。基于角度参数的概率LoS信道模型中信道功率期望和无人机飞行高度的关系如图4-2所示,从图中可以看出不同
d
2D
时
可以看成考虑了由NLoS链路造成的附加衰减因子的正则LoS概率。基于角度参数的概率LoS信道模型中信道功率期望和无人机飞行高度的关系如图4-2所示,从图中可以看出不同
d
2D
时
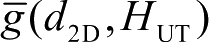 随着
H
UT
增大而变化的曲线。
随着
H
UT
增大而变化的曲线。
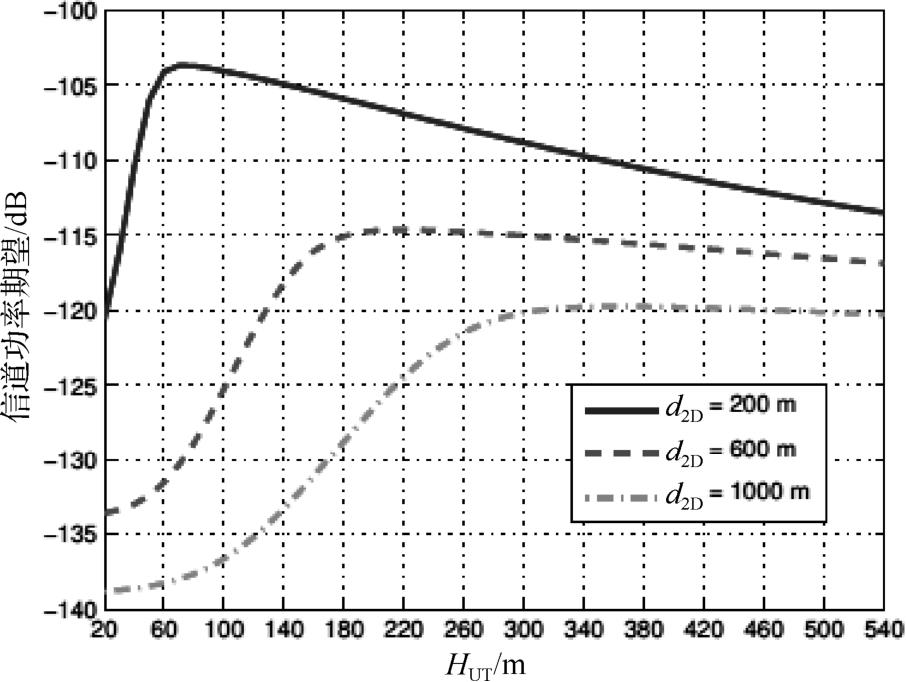
图4-2 基于角度参数的概率LoS信道模型中信道功率期望和无人机飞行高度的关系
在给定 d 2D 的条件下,由于LoS链路概率的增加,信道功率期望先随 H UT 的增大递增,当LoS链路概率的增加不能弥补由链路距离变长带来的路径损耗增量时,信道功率期望开始随 H UT 的增大而递减。这种对无人机飞行高度的折中已被广泛用于无人机机载基站/中继布局的优化中。
前面提到阴影衰落通常可以建模为一个空间对数正态过程,即:

式中, v ( x )是一个标准高斯过程; σ 是阴影标准差,受到载频、天线高度和传播环境等的影响。 v ( x )可用正弦波叠加法表示为:

式中,增益
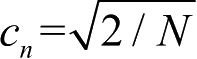 ;空间频率
s
n
=
f
n
/(
λ
n
f
max
);
θ
n
是独立同分布的随机变量,服从均匀分布
U
(0,2π)。于是可以求出
v
(
x
)的空间自相关函数,即:
;空间频率
s
n
=
f
n
/(
λ
n
f
max
);
θ
n
是独立同分布的随机变量,服从均匀分布
U
(0,2π)。于是可以求出
v
(
x
)的空间自相关函数,即:
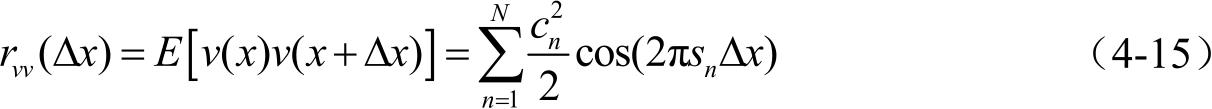
根据上面的公式可以将对数正态衰落过程 λ ( x )的空间自相关函数表示为:

式中, σ 0 = σ (ln10)/20。式(4-16)描述了距离的变化对阴影衰落的影响。
古德曼德森模型是一种典型的空间自相关函数模型,该模型借助实测数据对 v ( x )进了研究,通过负指数函数对 v ( x )的相关性进行了建模,可表示为:

式中,Δ x = x 2 -x 1 表示两个位置间的距离; D c >0表示去相关距离,即相关距离减少至一半或0时的距离。
古德曼德森模型的参数可以用等区域法(MEA)计算得出。根据随机过程的功率密度函数,通过MEA可获得古德曼德森模型的参数 s n 和 c n 的封闭形式的解。设 S vv ( s )表示随机过程的功率密度函数,对空间自相关函数 r vv ( x )进行傅里叶变换可得到功率谱密度函数,即:

定义
s
n
为离散空间频率,使得功率谱密度
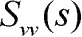 的积分等于l/(2
N
),即:
的积分等于l/(2
N
),即:

引入辅助函数:

可得:
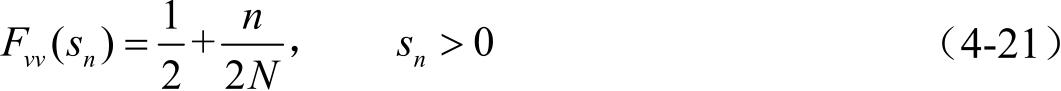
由式(4-18)和式(4-21)可得:

式中, n =1,…, N 。当 n = N 时, s n = ∞ ,为了避免这个问题,用 n -1/2代替 n ,式(4-22)可改写为:

由仿真模型的条件定义
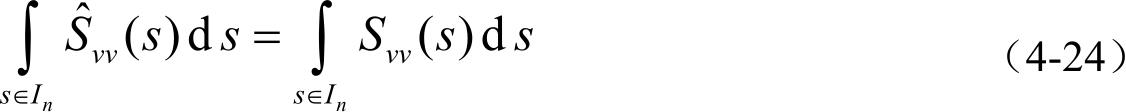
根据维纳-辛钦定理,由自相关函数
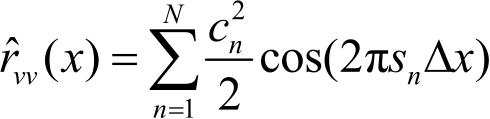
可得到功率谱密度为:
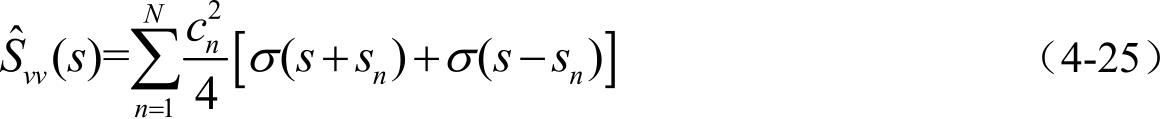
从而可得到
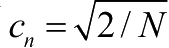 ,
n
=1,2,…,
N
。
,
n
=1,2,…,
N
。
由此可以得出古德曼德森模型的所有参数,即:
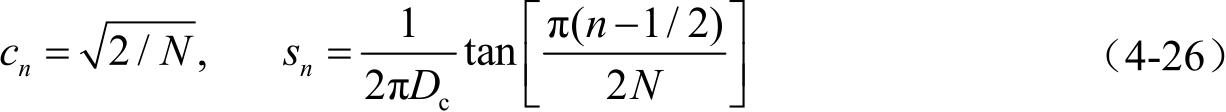
把得到的参数代入式(4-15)可以求得参数的具体数值。正弦曲线的数量 N 越大,采用MEA得到的仿真模型就越接近于参考模型。
古德曼德森模型存在一个问题,即:由于空间自相关函数的二阶导数是无限的,因此对数正态过程的电平通过率也是无限的。高斯模型就是为了解决这个问题而被提出的。将空间自相关函数表示为:

当空间自相关函数有确定的二阶导数时,参考模型的电平通过率
N
λ
(
r
)存在,反之则不存在。引入数值
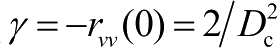 后,电平通过率可表示为:
后,电平通过率可表示为:
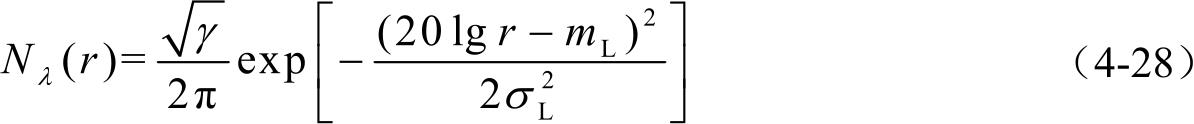
式中, σ L 和 m L 分别为阴影标准差和区域均值。和古德曼德森模型一样,采用MEA进行相似的推导过程,可得:

式中,erf -1 ( ⋅ )是逆误差函数。
巴特沃斯模型用含有 k 阶巴特沃斯滤波器的函数表示高斯过程 v ( x )的功率谱密度,即:

式中,
A
k
和
D
k
是取值为正的常数。
A
k
的取值要保证
v
(
x
)的平均功率∫
S
vv
(
s
)d
s
=1。根据维纳-辛钦定理可知,空间自相关函数可以由功率谱密度通过傅里叶逆变换获得,因此古德曼德森模型实际上是巴特沃斯模型在
k
=1、
A
1
=2
D
c
、
D
1
=2π
D
c
时的一个特例。当
k=
2、
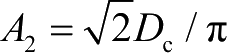 时可得到二阶巴特沃斯模型,此时
v
(
x
)的空间自相关函数为
时可得到二阶巴特沃斯模型,此时
v
(
x
)的空间自相关函数为
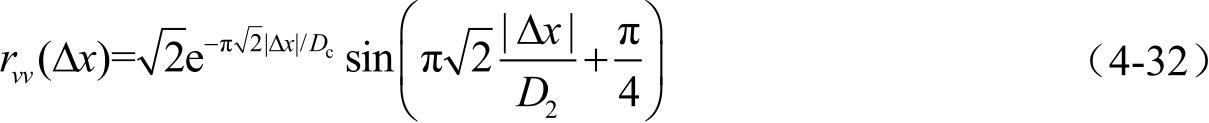
由此可得
γ
=
-γ
vv
(0)=(2π/
D
2
)
2
。注意:当
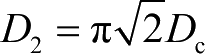 时,二阶巴特沃斯模型和古德曼德森模型有相同的电平通过率。
时,二阶巴特沃斯模型和古德曼德森模型有相同的电平通过率。