1.3
常用计数制之间的转换

不同进制之间进行转换应遵循转换原则。转换原则是：两个有理数如果相等，则有理数的整数部分和小数部分一定分别相等。也就是说，若转换前两数相等，转换后仍必须相等，数制的转换要遵循一定的规律。

1.3.1
二、八、十六进制数转化成十进制数

二转十

将二进制数转换成十进制数，只要将二进制数用计数制通用形式表示出来，计算出结果，便得到相应的十进制数。

八转十

八进制—>十进制：以8为基数按权展开并相加。

例：

把（652.34） ₈ 转换成十进制。

十六转十

十六进制—>十进制：以16为基数按权展开并相加。

例：将（19BC.8） ₁₆ 转换成十进制数。

1.3.2
十进制转换成二进制

整数部分的转换

整数部分的转换采用的是除2取余法。其转换原则：将该十进制数除以2，得到一个商和余数（K ₀ ），再将商除以2，又得到一个新商和余数，如此重复，直到得到商为0和余数（K _n-1 ），然后将所得到的各位余数，以最后余数为最高位，最初余数为最低位依次排列，即K _n-1 K _n-2 …K ₁ K ₀ 。这种方法又称为“倒序法”。

例如：将（126） ₁₀ 转换成二进制数。

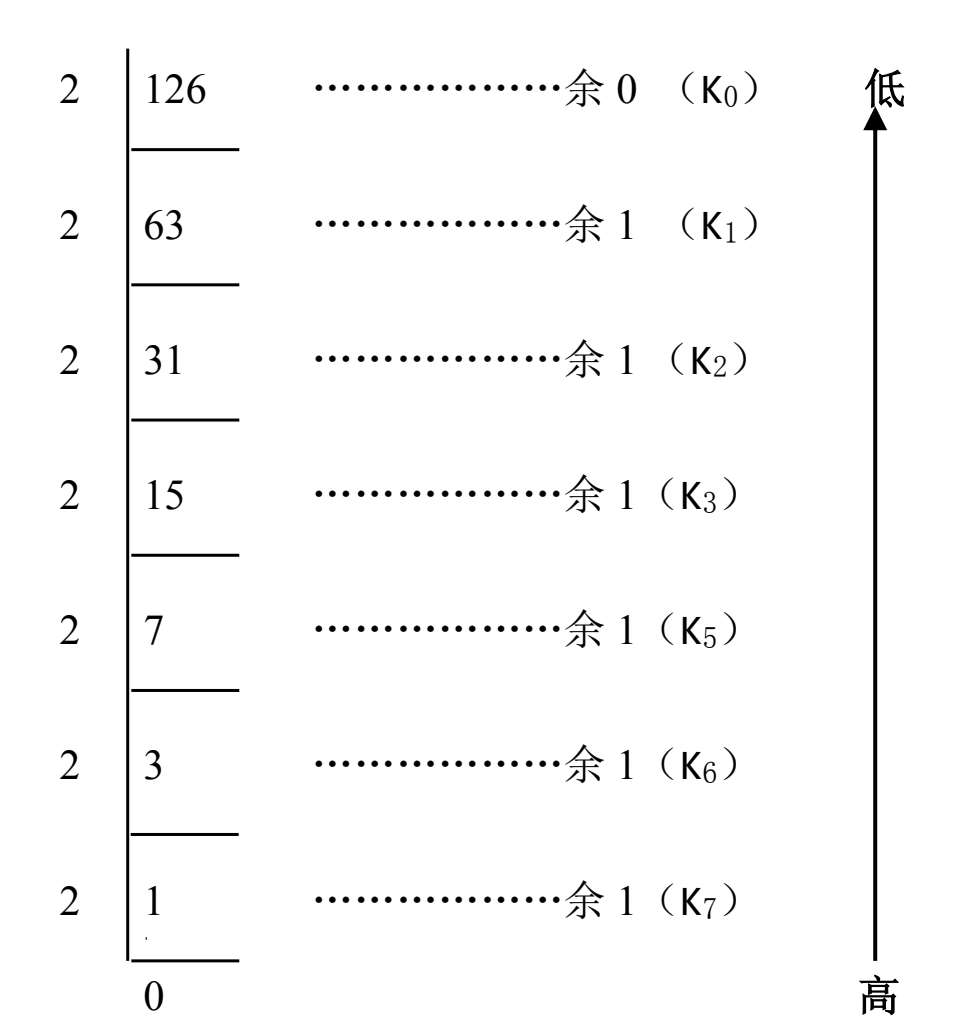
结果为：（126） ₁₀ = （1111110） ₂

小数部分的转换

小数部分的转换采用乘2取整法。其转换原则是：将十进制数的小数乘以2，取乘积中的整数部分作为相应二进制数小数点后最高位K _-1 ,反复乘2，逐次得到K _-2 、K _-3 …….K _-n ，直到乘积的小数部分为0或1的位数达到精确要求为止。然后把每次乘积的整数部分由上而下依次排列起来（K _-1 K _-2 ……K _-n ），即是所求的二进制数。这种方法又称为“顺序法”。

例如：将十进制数（0.125） ₁₀ 转换成相应的二进制数。

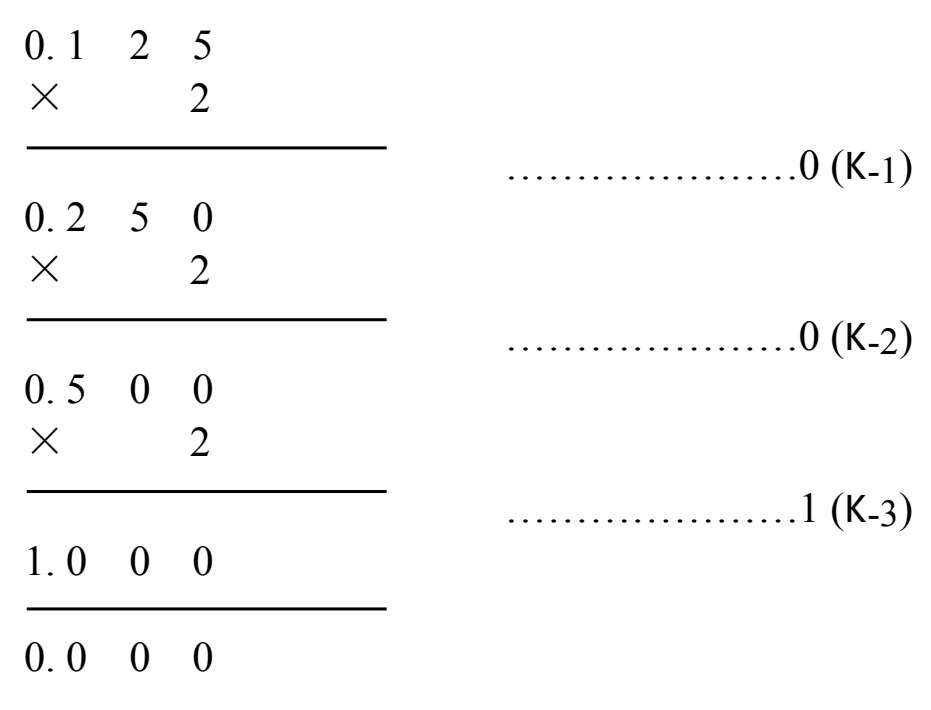
结果为：（0.125） ₁₀ =（0.001） ₂

例如：（50.25） ₁₀ 转换成二进制数。

分析：这个数又有整数又有小数，可将其整数和小数分别转换成二进制，然后再把两者连接起来即可。

分别计算出它们的整数和小数

（50） ₁₀ =（110010） ₂

（0.25） ₁₀ =（0.01） ₂

结果：（50.25） ₁₀ =（110010.01） ₂

1.3.3
八进制与二进制之间的转换

八转二

八进制转换成二进制数所使用的转换原则是“一位拆三位”，即把一位八进制数对应于三位二进制数，然后按顺序连接即可。

例：将（64.54） ₈ 转换为二进制数。

结果为：（64.54） ₈ = （110100.101100） ₂

二转八

二进制转换成八进制数可概括为“三位并一位”，即从小数点开始向左右两边以每三位为一组，不足三位时补0，然后每组改成等值的一位八进制数即可。

例如：将（110111.11011） ₂ 转换成八进制数。

结果为：（110111.11011） ₂ =（67.66） ₈

1.3.4
二进制与十六进制之间的转换

二转十六

二进制数转换成十六进制数的转换原则是“四位并一位”即以小数点为界，整数部分从右向左每四位为一组，若最后一组不足4位，则在最高位前面添0补足4位，然后从左边第一组起，将每组中的二进制数按权数相加得到对应的十六进制数，并依次写出即可；小数部分从左向右每4位为一组，最后一组不足4位时，尾部用0补足4位，然后按顺序写出每组二进制数对应的十六进制数。

例：将（1111101100.0001101） ₂ 转换成十六进制数。

结果为：（11111011.0001101） ₂ =（3EC.1A） ₁₆

十六转二

十六进制转换成二进制数的转换原则是“一位拆四位”，即把1位十六进制数写成对应的4位二进制数，然后按顺序连接即可。

例：将（C41.BA7） ₁₆ 转换成二进制数。

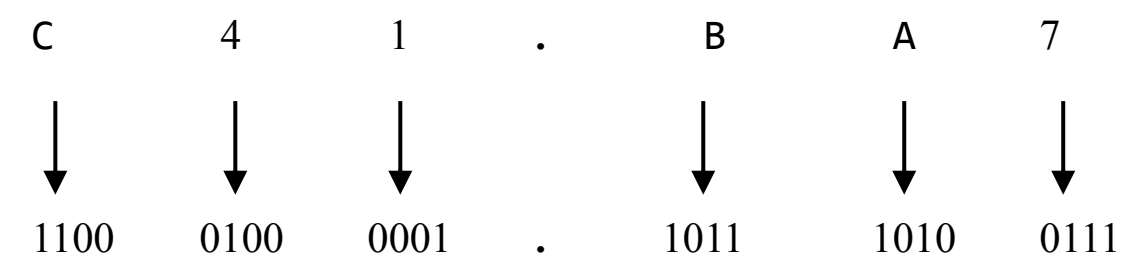
结果为：（C41.BA7） ₁₆ = （110001000001.101110100111） ₂ iBjd986jhuCLaVg6Il8uncUctpqrCiOMY6gr7TvDhJYMhQoGOmtEUxP+SC9LZAjC