




棱柱分为直棱柱(侧棱与底面垂直)和斜棱柱(侧棱与底面倾斜)。底面为止多边形的直棱柱,称为正棱柱。现以正六棱柱为例讨论作其三面投影图的方法。
由如图3.2所示可知,正六棱柱包括8个外表面。其中上下两表而分别被称为上下底面,它们为全等的正六边形且互相平行;6个矩形外表面称为侧面或棱面,它们全等且与底面垂直;6条棱线相互平行、长度相等H与上、下底面垂直。
如图3.2所示可以看出,其三面投影分别如下。
(1) 水平投影为一正六边形,它是上、下底面的投影(重影),且反映实形;六边形的各边为6个侧面的积聚投影;6个角点是6条侧棱的积聚投影。
(2) 正面投影是并列的3个矩形线框,中间的矩形线框是棱柱前后侧面的投影(重影),反映实形;左右的线框是其余4个侧面的投影,为类似形;线框上下两条水平线是上下底面的积聚投影;4条竖直线是侧棱的投影,反映实长。
(3) 侧面投影是并列的两个矩形线框,它是棱柱左右4个侧面的投影(雨影),为类似形;两侧竖直线是棱柱前后侧面的积聚投影间的竖直线是棱的投影;上下水平线则为底面的积聚投影。
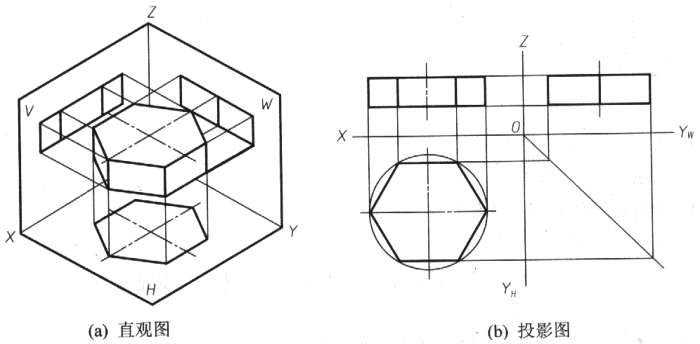
图3.2
通过上述分析,可以总结出棱柱体的视图特征如下。
(1) 反映底面实形的视图为多边形。
(2) 另两种均为矩形(或矩形的组合图形)。
由此可得出以下结论:基本体中柱体的投影特征可归纳为 “矩矩为柱” 四个字。这句话的含义是:只要是柱体,则必有两个投影的外线框是矩形;反之,若某一物体两个投影的外线框都是矩形,则该物体一定是柱体。而第三个投影可用来判别是何种柱体。
工程形体的形状为棱柱者居多,如图3.3所示的四种工程形体的投影图,读者可以自行分析。
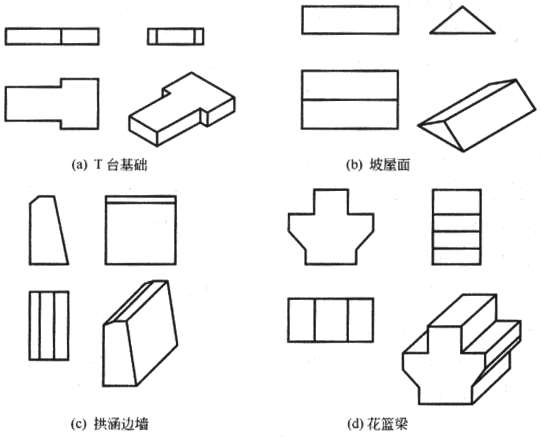
图3.3
具体作图步骤如下。
(1) 研究平面体的几何特征,决定安放位置即确定正面投影方向,通常将形体的表面尽量平行于投影面。
(2) 分析该形体三面投影的特点。
(3) 布图(定位),画出基准线。
(4) 先画出反映形体底面实形的投影,再根据投影关系画出其他投影。
(5) 检查、整理加深,标注尺寸,如图3.4所示。
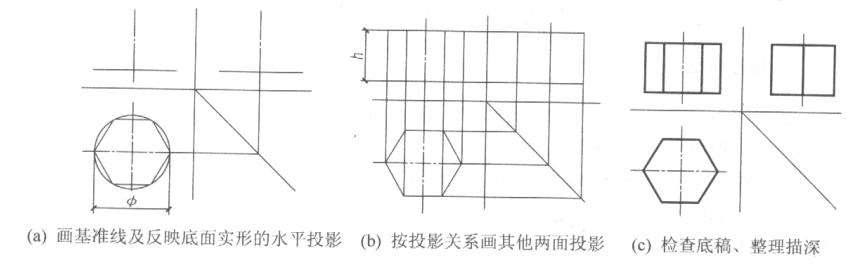
图3.4
底面为正多边形,各侧面为具有公共顶点的全等等腰三角形的棱锥称正棱锥,其锥顶在过底面中心的垂线上。现以正三棱锥为例讨论作其三面投影图的方法。
正三棱锥又称四面体,如图3.5所示为正二棱锥的投影图。其底面为正三角形,三个棱面为三个全等的等腰三角形。
由图3.5可以看出,其三面投影分别如下。
(1) 水平投影中的外形正三角形是底面的投影,反映实形;s是锥端的投影,位于三角形abc的中心,它与3个角点的连线s、sb、sc是3条侧棱的投影;中间3个小三角形是3个侧面的投影。
(2) 正面投影是两个并列的全等三角形,是三棱锥3个侧面的投影。底面及侧棱的正面投影,读者可自行分析。
(3) 侧面投影是一个非等腰三角形,s "a "(c')为三棱锥后侧面的积聚投影,s"b"为三棱锥侧棱的投影,其余部分的投影读者可自行分析。
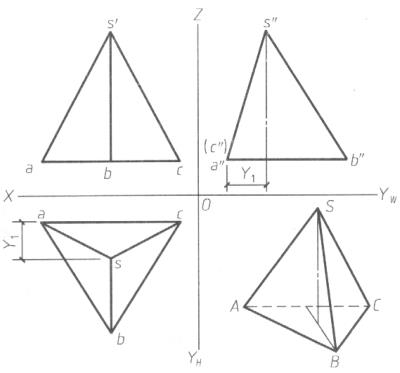
图3.5
通过上述分析可以是结出棱锥体的投影特征如下:
(1) 反映底面实形的视图为多边形(内含反映侧表面的几个三角形)。
(2) 另两视图为并列的三角形(或三角形的组合图形)。
由此可得出以下结论:基本体中锥体的投影特征可归纳为四个字:“三三为锥”,即若物体有两面投影的外线框均为三角形,则该物体一定是锥体;反之,凡是锥体,则必有两面投影的外线框为三角形。同样,第三个投影可用来判别是何种锥体,棱锥体的投影特征如图3.6所示。
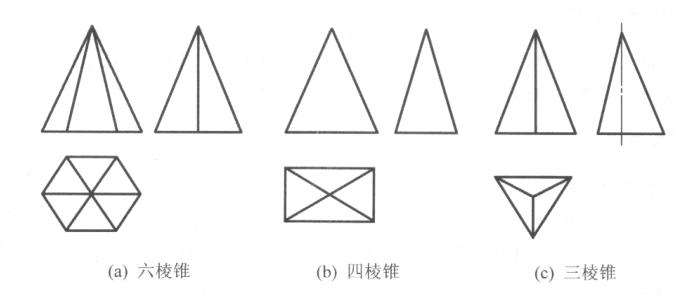
图3.6
作图方法和步骤与棱柱体的作图方法及步骤基本相同。如图3.7所示为正五棱锥投影图的作图步骤(已知底面多边形外接圆直径及锥高h)。
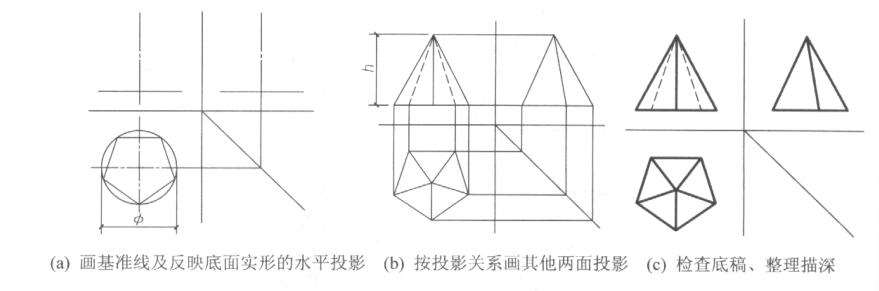
图3.7
棱台可看作由棱锥用平行于锥底面的平面截去锥顶而形成的形体,上、下底面为各对应边相互平行的相似多边形,侧面为梯形,如图3.8所示。
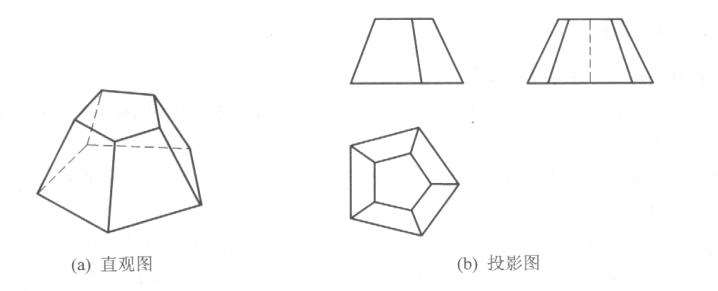
图3.8
图中五棱台的底面为水平面,左侧面为正垂面,其他侧面是一般位置平面。
可以看出,棱台的视图特征是:反映底面实形的视图为两个相似多边形和反映侧面的几个梯形,另外两视图为梯形(或梯形的组合图形)。因此亦有“梯梯为台”之说。