




以立方体为例,只要离画幅最近的是立方体的一个角,那么立方体左右两个竖立面必然与画幅呈一定角度,且两角相加为90°,在这种情形下作图称为成角透视。由于它有两个消失点,两个角互为余角,所以又叫“二点透视”“余角透视”。(图4.1 A、B)
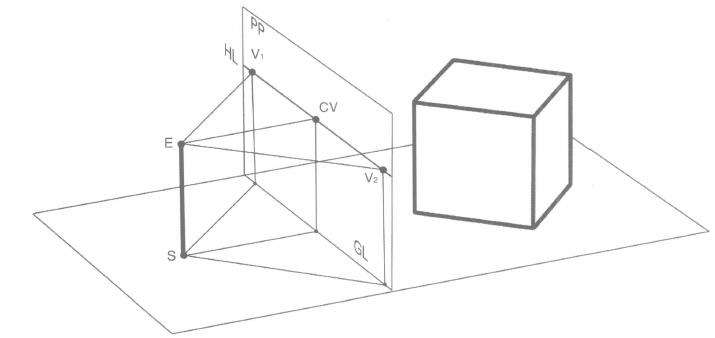
图4.1 A
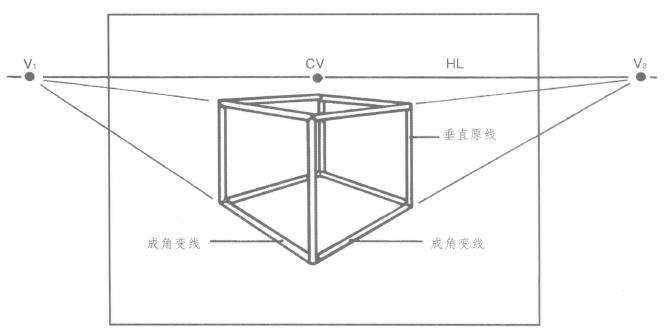
图4.1 B
(1)边线为平行于画面的垂直原线,透视方向不变,仍然垂直,没有灭点,但有近大远小的透视变化。(图4.1B、图4.2)
(2)边线为平行于基面的成角变线,左右各一组,水平消失方向不一,形成两个灭点,都在视平线上。(图4.1B、图4.3)
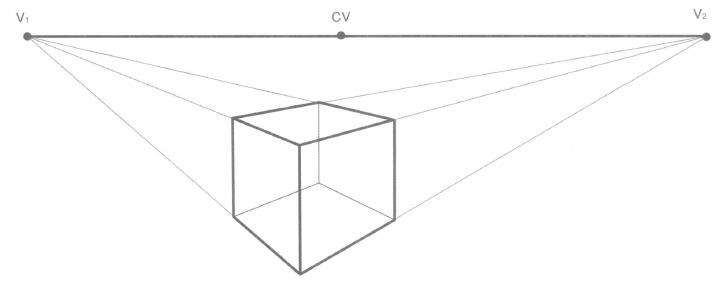
图4.2
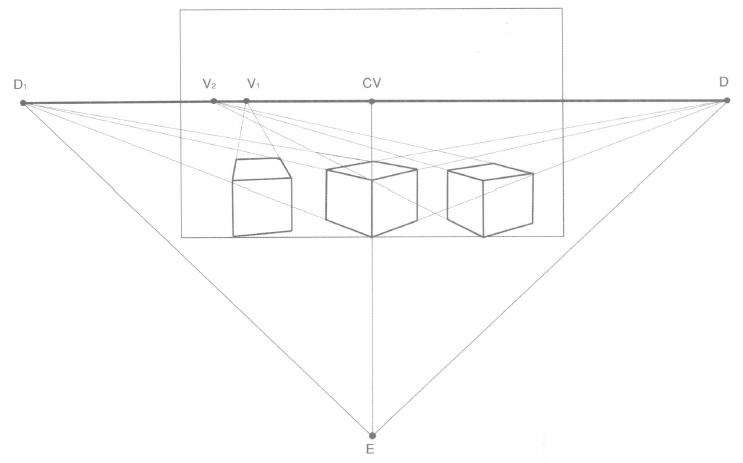
图4.3
(1)在同一视域中,由于立方体与画面所成的角度不同,决定了成角透视的灭点在视平线上的位置是可移的。(图4.3)
(2)同一立方体左右两组成角边形成的两个灭点处在主点两侧。当立方体成角边与画面成45°角时,两个灭点即左右距点;当立方体成角边与画面成非45° 也非90°角时,一个余点处在同侧距点之内,另外一个余点处在同侧距点之外,两个余点到主点的距离成反比。(图4.3)
(3)立方体上下移动时,越接近视位高度,顶、底面两组成角边间的前后夹角越大,体积越平缓。当立方体顶面或底面与视位等高时,该面两组成角边的前后夹角称为平角,贴于视平线而越远离视平线,前后夹角越小,体积感越强。(图4.4)
(4)立方体作深度排列时,体积由大变小,而顶、底面两组成角边间的前后夹角由小变大,越远越平缓,彼此出现形体差异。(图4.4)
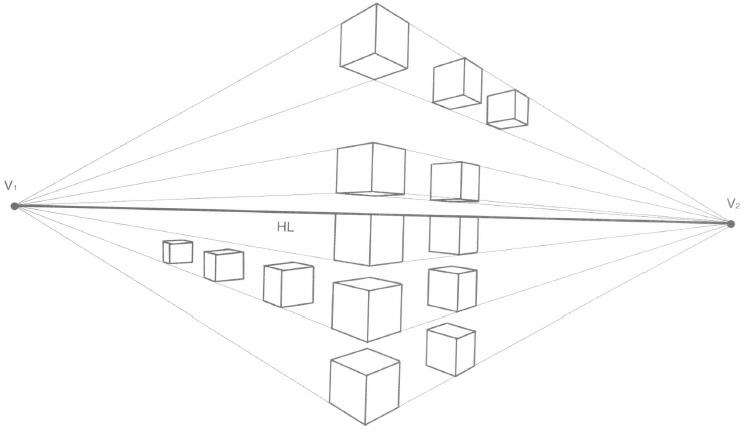
图4.4