




作透视图的实质就是如何表现各种线段在纵深关系中的距离和长度的变化。在透视的纵深关系中,不同透视方向的线段有两类:一类是与画面成垂直关系的线段,另一类是与画面成倾斜关系的线段。平行透视图中,测定与画面垂直的线段透视长度可采用距点法。
距点法是运用距点来测量的方法,就是利用45°直角三角形原理,在平行透视图上测量垂直于画面线段长度的画法。在平行透视中,距点有两个,用“D”表示,分别在主点左、右视平线上。距点到主点的距离与视点到主点的距离相等,如图3.4所示。
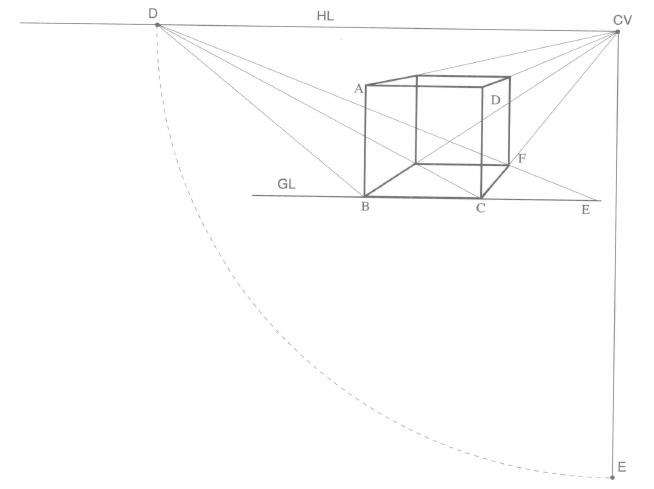
图3.4
距点到主点的远近等于视点的远近,它影响到透视图进深程度的表现。距点远,进深显得平缓;距点近,进深显得长。
作图步骤:
(1)定视点E,视平线HL,主点CV。画与画面平行的正方形ABCD。从ABCD 各引消失线至主点CV。
(2)延长BC 线得E点,BC=CE。由E点引线至距点D 得F点(即CCV 线与ED 线交叉点),CF 之长就是正方形伸向远方的透视长(深)度。
(3)由F点分别连接作垂直、水平线与DCV、BCV、ACV 各线相交,各点连接形成方体,即正方体的平行透视图。
作图步骤:
以一个宽4米、高3米、深5米的房间为例,画面中的比例为4∶ 3∶ 5。
(1)定出视平线HL,主点CV,按比例定出宽度尺寸AB,AB 线段位于基线上,过CV 作A、B 及各点的连线,确定距点D,DCV 的距离等于视距,如图3.5A所示。
(2)按比例作AB 两点的垂直线,AD、BC 即房间的真高线,连接DCV、CCV。在AB延长线上确定0点,BO线等于一个刻度。过点O作距点D 的连线,与视心CV 的各透视线形成交点,作各交点的水平线与ACV、BCV相交,如图3.5B所示。
(3)继续作垂直线、水平线,完成房间室内空间透视结构图,如图3.5C所示。
图3.5A
图3.5B
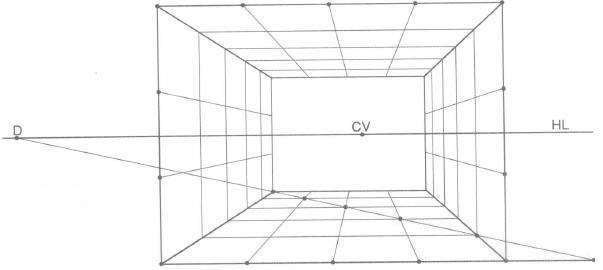
图3.5C
作图步骤:
(1)将准备好的平面图按1米× 1米画上网格作为辅助线,如图3.6A所示。
(2)按室内实际比例尺寸4米宽、3米高确定房间外框,并标上刻度。设定GL 线、HL 线、CV点和距点D。分别过CV点作A、B和0、l、2、3、4 各点的连线,过D点分别作0、1、2、3、4 各点的连线,如图3.6B所示。
(3)过4CV 线上各交点分别作水平和垂直线,完成室内空间结构图,如图3.6C所示。
(4)根据平面图中家具在网格中的位置,在透视图中找到相应的地面投影,如图3.6D所示。
(5)过地面家具投影的各点作垂直线,通过真高线寻求家具的真实高度和形状,如图3.6E所示。
(6)家具的高度和形状求得后,进行细节处理,画出各家具的形象特征,完成室内平行透视效果图,如图3.6F所示。
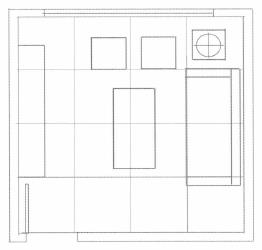
图3.6A
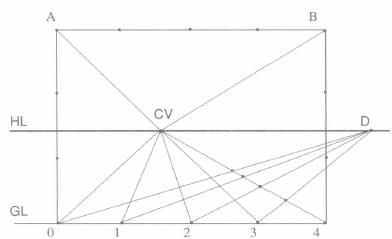
图3.6B
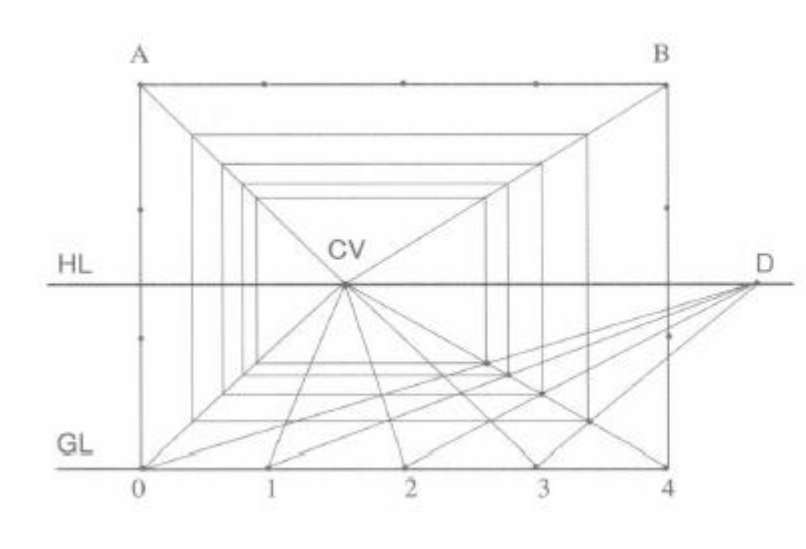
图3.6C
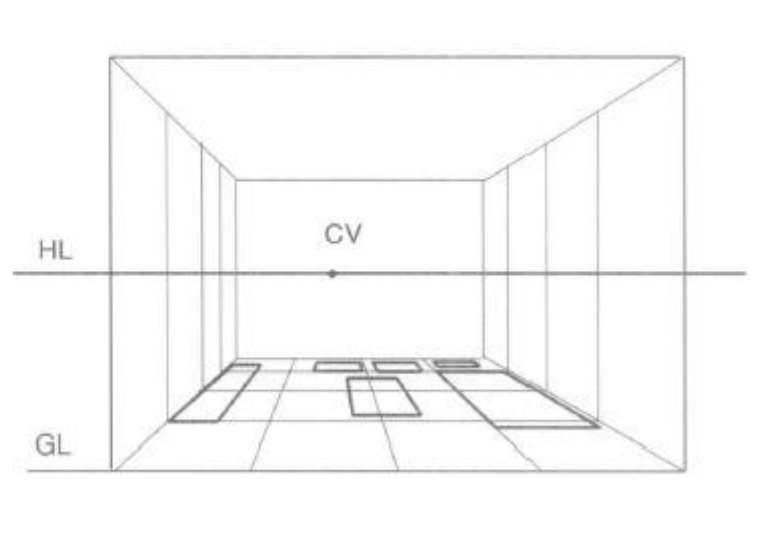
图3.6D
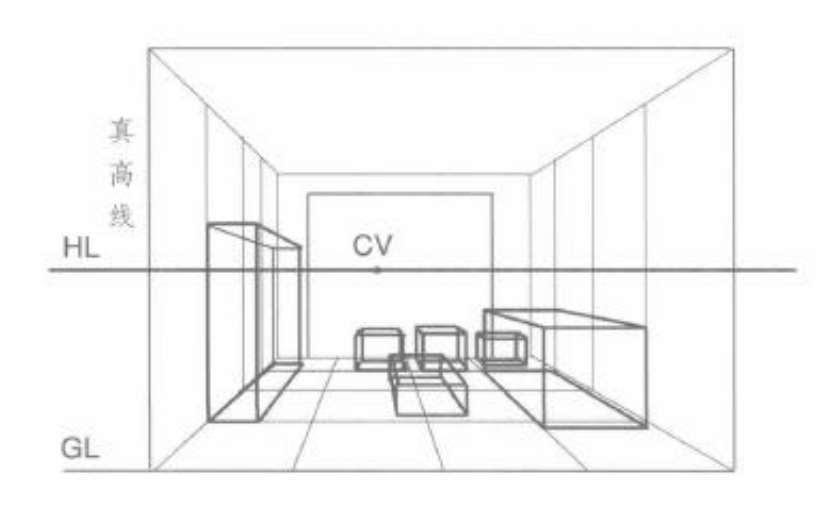
图3.6E
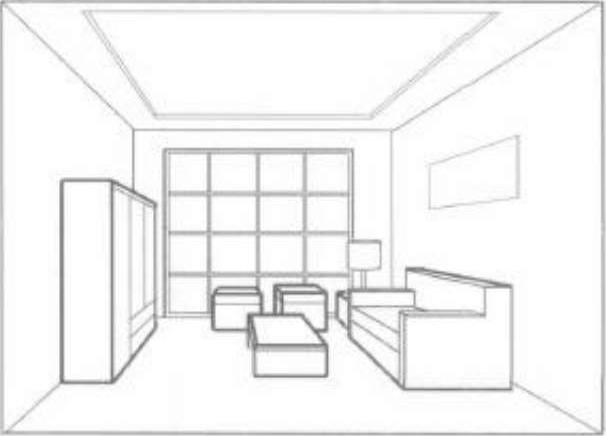
图3.6F
平行透视中,方形物三组棱边分别是宽度、高度、深度,它们的透视方向是:水平、垂直、向主点。这也是多件方形物组成平行透视场景的线段的透视方向。利用这个规律,可以快速画出平行透视场景的近似图。
(1)如图3.7A所示:在画面上确定视平线、主点,设想画面上布满由横线、竖线和从主点引出的辐射线组成的网格,并用虚线画出。
(2)如图3.7B所示:任何平行透视景物,无论是简单的还是复杂的,它们的轮廓线都“隐藏”在网格线条中,找出它们的位置。
(3)如图3.7C所示:沿网状线条三种方向,确定每件物体的形状并勾画出其轮廓线。
最后,添加细节,去掉多余的线条,完成平行透视近似图。
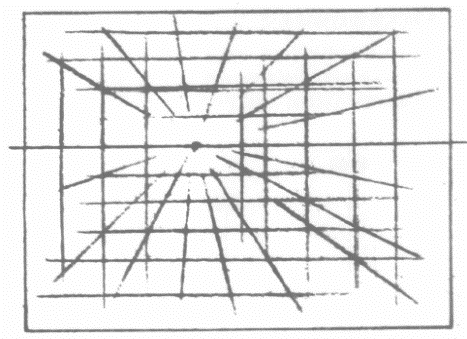
图3.7A
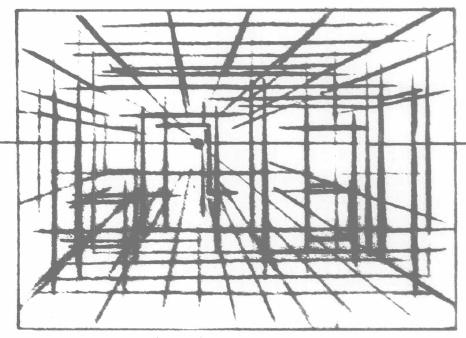
图3.7B

图3.7C
如图3.8所示。先画最近的第一根灯杆,从顶端和底端对CV点作灭线,确定灯杆高低范围,再从灯杆二分之一处对CV点作灭线。根据需要(或按实际比例)画第二根杆,过第一根杆顶端经第二根杆中点画直线,相交于杆底端灭线的点就是第三根杆的位置。
照此类推,画出第四、五、六根灯杆。
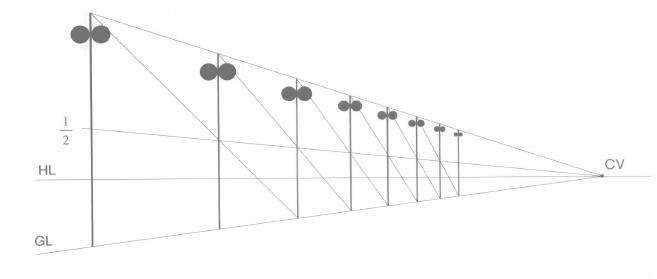
图3.8
在画面上确定视平线、主点和距点。选择视高约2人高,等于一层楼的高度;人物等于1/2 视高,客车宽度等于3 /4 视高,人行道AB 宽度与视高相等。
(1)连线点A 至距点D,与B 至主点CV 的线段相交,交点是店面CD 的深度;以同样方法求出店面②、③的深度。
(2)远处人行道转角C点是人行道的宽度,仍为2人高。以此为准,连线CE,得马路宽度,为16人高;自中点M 连线CV 并反向延长,为马路中线。连线MD 交E 至主点于F,EF是马路十字路口深度。
(3)客车的宽度已知,深度以同样的方法求出;远处电线杆高度为4人高,等于两层楼高度,用“等距离景物透视画法”求出各相同高度电线杆的位置。
(4)得出透视框架后,添加细节,最后完成室外透视图,如图3.9所示。
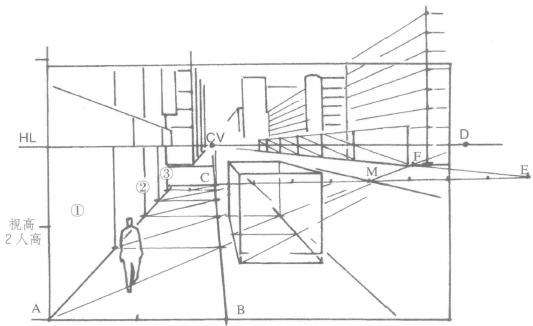
图3.9A

图3.9B
(1)如图3.10A:距点过近,正方形图像失真,图3.10B 为正确图。
(2)如图3.11A、3.11B:平行透视各消失点不统一,平行透视各消失点不在一条视平线上,3.11C 为正确图。
(3)如图3.12:线和面应有透视变化的没有,不应有透视变化的反而有了;物体未画平,后方或侧方高于另一方,图3.12B 为正确图。
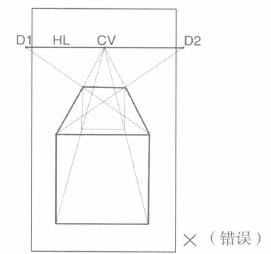
图3.10A
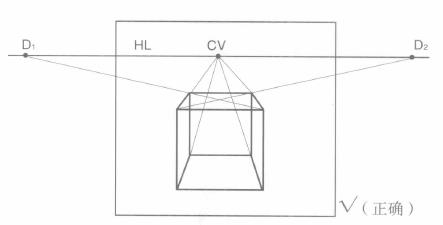
图3.10B
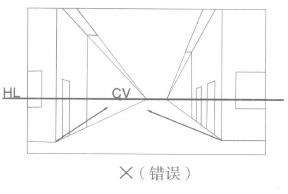
图3.11A
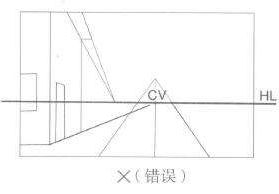
图3.11B
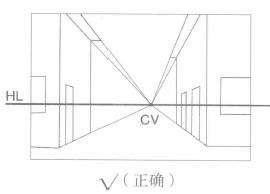
图3.11C
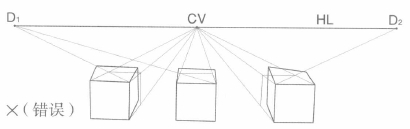
图3.12A
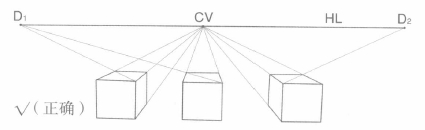
图3.12B