




(1)空间直角坐标系
为了确定平面上一点的位置,我们建立了平面直角坐标系.同样地,为了确定空间内任意一点的位置,就需要建立空间直角坐标系.
在空间任意取定一点
O
,以点
O
为原点,作 3 条相互垂直的数轴,
x
轴,
y
轴,
z
轴,这样就构成了空间直角坐标系
Oxyz.
一般地,
x
轴,
y
轴放置在水平面上,那么
z
轴垂直于水平面,且
x
轴,
y
轴,
z
轴的正方向要符合右手法则,即伸出右手,让四指与大拇指垂直,当右手 4 个手指从
x
轴正向以
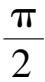 角度转向
y
轴正向时,大拇指的方向就是
z
轴的正向(图 2.2).3条坐标轴中的任意两条可以确定一个平面,这样确定的平面称为坐标面,由
x
轴和
y
轴所确定的坐标面称为
xOy
面,另两个由
y
轴和
z
轴,
z
轴和
x
轴所确定的平面分别称为
yOz
面和
zOx
面.3 个坐标面把空间分为 8 个部分,每个部分为一个卦限.含
x
轴,
y
轴,
z
轴正向的卦限称为第Ⅰ卦限,然后逆着
z
轴正向看时,按逆时针顺序依次为Ⅱ,Ⅲ,Ⅳ卦限,位于Ⅰ,卦限的下面的 4 个卦限,依次为Ⅴ,Ⅵ,Ⅶ,Ⅷ卦限(图 2.3).
角度转向
y
轴正向时,大拇指的方向就是
z
轴的正向(图 2.2).3条坐标轴中的任意两条可以确定一个平面,这样确定的平面称为坐标面,由
x
轴和
y
轴所确定的坐标面称为
xOy
面,另两个由
y
轴和
z
轴,
z
轴和
x
轴所确定的平面分别称为
yOz
面和
zOx
面.3 个坐标面把空间分为 8 个部分,每个部分为一个卦限.含
x
轴,
y
轴,
z
轴正向的卦限称为第Ⅰ卦限,然后逆着
z
轴正向看时,按逆时针顺序依次为Ⅱ,Ⅲ,Ⅳ卦限,位于Ⅰ,卦限的下面的 4 个卦限,依次为Ⅴ,Ⅵ,Ⅶ,Ⅷ卦限(图 2.3).
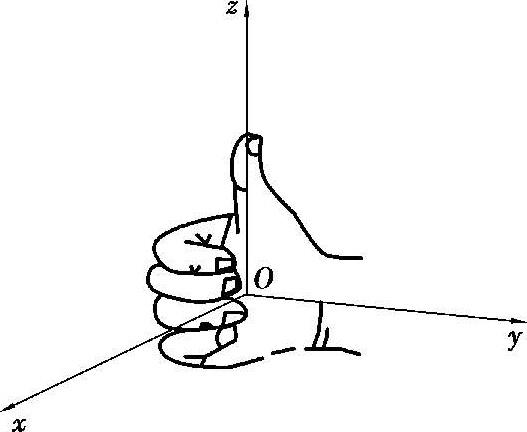
图 2.2
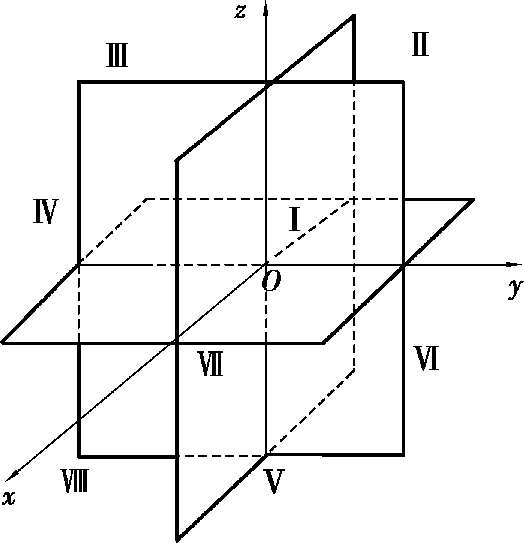
图 2.3
建立了空间直角坐标系,就可以建立空间点与有序数组之间的对应关系.
设 M 为空间任意一点,过 M 作 3 个分别垂直于 x 轴, y 轴, z 轴于点 P , Q , R 的平面,这 3个点在其上的坐标分别为 x , y , z ,于是,空间一点 M 就唯一确定了一个有序数组( x , y , z );反过来,对于某个有序数组( x , y , z ),我们可以在 x 轴, y 轴, z 轴分别取点 P , Q , R ,使 OP = x , OQ = y , OR = z ,然后过 P , Q , R 3 点分别作垂直于 x 轴, y 轴, z 轴的平面,这 3 个平面交于一点 M ,则由一个有序数组( x , y , z )唯一地确定了一点 M. 于是,通过空间直角坐标系,我们就建立了空间的点 M 和有序数组( x , y , z )之间的一一对应关系,有序数组( x , y , z )称为点 M 的坐标,记为 M ( x , y , z )(图 2.4).
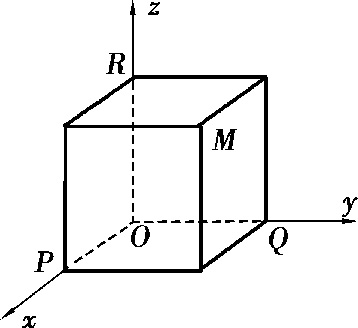
图 2.4
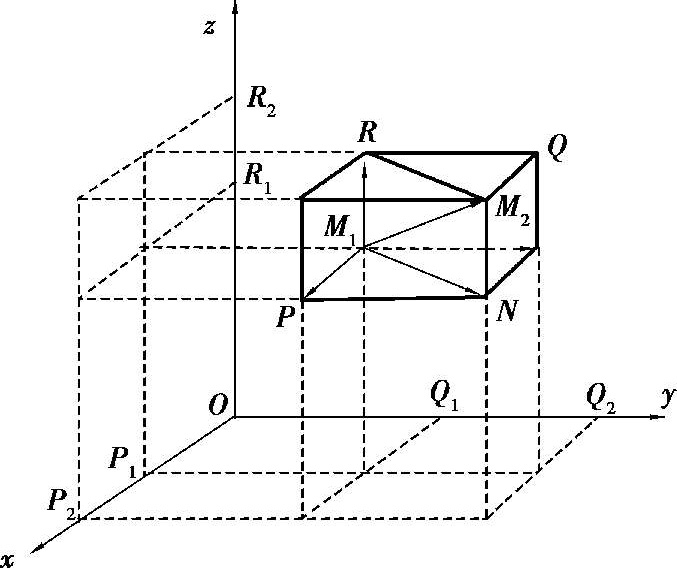
图 2.5
(2)空间两点的距离
设
M
1
(
x
1
,
y
1
,
z
1
),
M
2
(
x
2
,
y
2
,
z
2
)为空间中的两个点,过
M
1
,
M
2
各作 3 个分别垂直 3 条坐标轴的平面,这 6 个平面围成一个以
M
1
M
2
为对角线的长方体,如图 2.5 所示由于△
M
1
NM
2
为直角三角形,∠
M
1
NM
2
为直角,所以
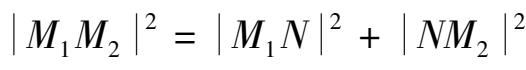 ,又因△
M
1
PN
也是直角三
,又因△
M
1
PN
也是直角三
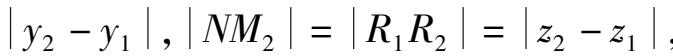 角形,
角形,
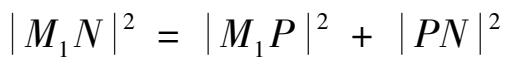 ,所由以于
,所由以于
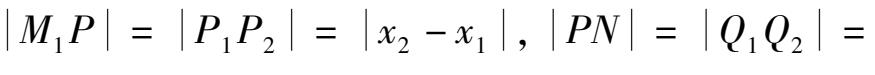
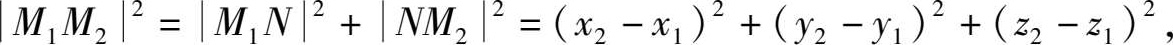
即
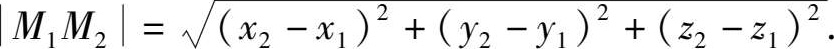
例 2.1 求证以 M 1 (4,3,1), M 2 (7,1,2), M 3 (5,2,3)3 点为顶点的三角形是一个等腰三角形.
解 因为
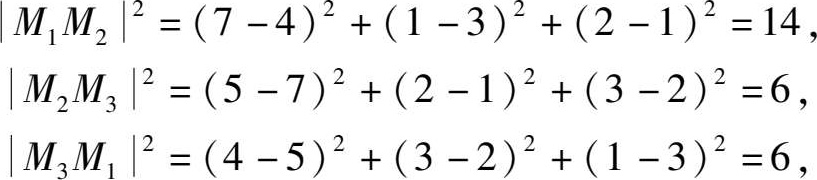
所以
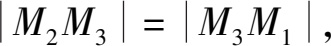
即△ M 1 M 2 M 3 为等腰三角形.
在平面解析几何中,我们把平面曲线看成是平面上按照一定规律运动的点的轨迹.类似地,在空间解析几何中,我们把曲面看成是空间中按照一定规律运动的点的轨迹.空间中的点按照一定规律运动,它的坐标( x , y , z )就满足 x , y , z 的某个关系式,这个关系式就是曲面方程,记为 F ( x , y , z )=0.
定义2.1 如果曲面 S 与三元方程 F ( x , y , z )=0 有下列关系:
①曲面 S 上任意一点的坐标都满足方程 F ( x , y , z )=0;
②不在曲面 S 上的点的坐标都不满足方程 F ( x , y , z )=0.
那么,方程 F ( x , y , z )=0 就叫作曲面 S 的方程,而曲面 S 就叫作方程 F ( x , y , z )=0 的图形(图 2.6).
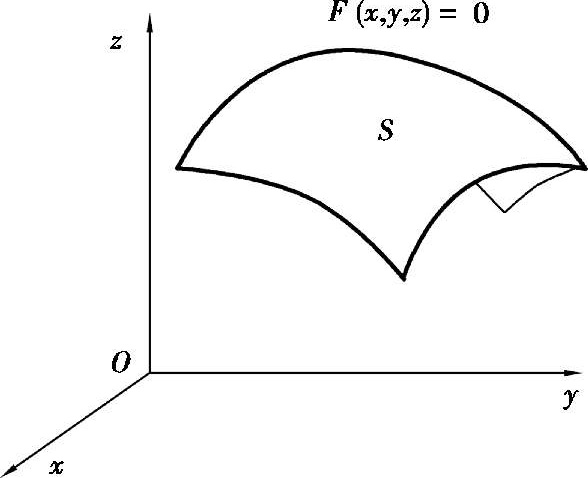
图 2.6
例 2.2 建立球心在 M 0 ( x 0 , y 0 , z 0 ),半径为 R 的球面的方程.
解 设 M ( x , y , z )是球面上的任一点,那么
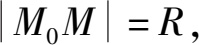
即
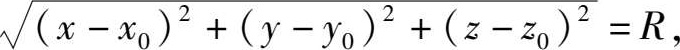
或
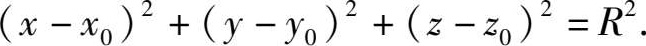
特别地,如果球心在原点,那么球面方程为
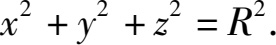
例 2.3 设有点 A (1,2,3)和 B (2,-1,4),求线段 AB 的垂直平分面的方程.
解 由题意知,所求的平面就是与 A 和 B 等距离的点的轨迹.
设所求平面上的任意一点为 P ( x , y , z ),由于 AP = BP ,所以
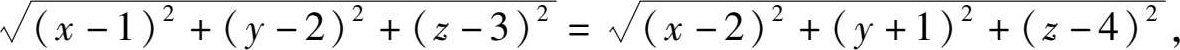
即 2 x -6 y + 2 z -7 = 0 为所求平面方程.
例
2.4 直线
L
绕一条与
L
相交的直线旋转一周,所得的旋转曲面称为圆锥面,两直线的交点称为圆锥面的顶点,两直线的夹角
α
(0<
α
<
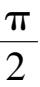 )称为圆锥面的半顶角.求顶点在坐标原点
O
,旋转轴为
z
轴,半顶角为
α
的圆锥面的方程.
)称为圆锥面的半顶角.求顶点在坐标原点
O
,旋转轴为
z
轴,半顶角为
α
的圆锥面的方程.
解
在
y
O
z
坐标面上,直线
L
的方程为
z
=
y
cot
α
,因为旋转轴为
z
轴,所以在直线方程中将
y
改成
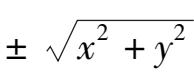 ,便得到所求圆锥面的方程
,便得到所求圆锥面的方程
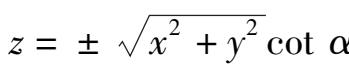 .
.
我们可以用Mathematica方便地作出该方程所表示的曲面,其命令语法格式及其意义:
①命令语法格式:ContourPlot3D[f = = g,{x,a,b},{y,c,d},{z,e,f}].
意义:绘制方程 f ( x , y , z )= g ( x , y , z )在区域{( x , y )| a ≤ x ≤ b , c ≤ y ≤ d , e ≤ z ≤ f }的图形.
②命令语法格式:RevolutionPlot3D[f,{x,x 1 ,x 2 }].
意义: x O z 平面上的曲线 z = f ( x )绕 z 轴旋转一周形成的曲面.
③命令语法格式:RevolutionPlot3D[f,{x,x 1 ,x 2 },RevolutionAxis→{a,b,c}]
意义: x O z 平面上的曲线 z = f ( x )以起点在原点的向量{ a , b , c }为轴旋转.
例 2.5 绘制由方程 x 2 + y 2 + z 2 = 1 所确定的图形.
解 In[1]:= ContourPlot3D[x^2 + y^2 + z^2 = = 1,{x,-1,1},{y,-1,1},{z,-1,1}]
Out[1]=
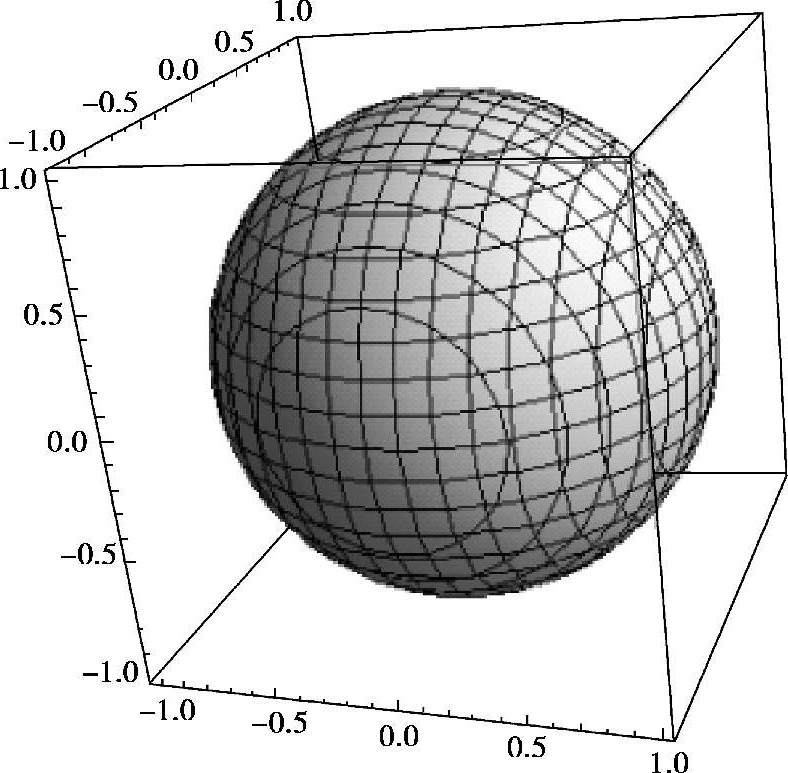
例 2.6 作正弦曲线 z = sin x, x ∈[0,2π]绕 z 轴旋转一周形成的曲面.
解 In[1]:= RevolutionPlot3D[sin[x],{x,0,2π}
Out[1]=
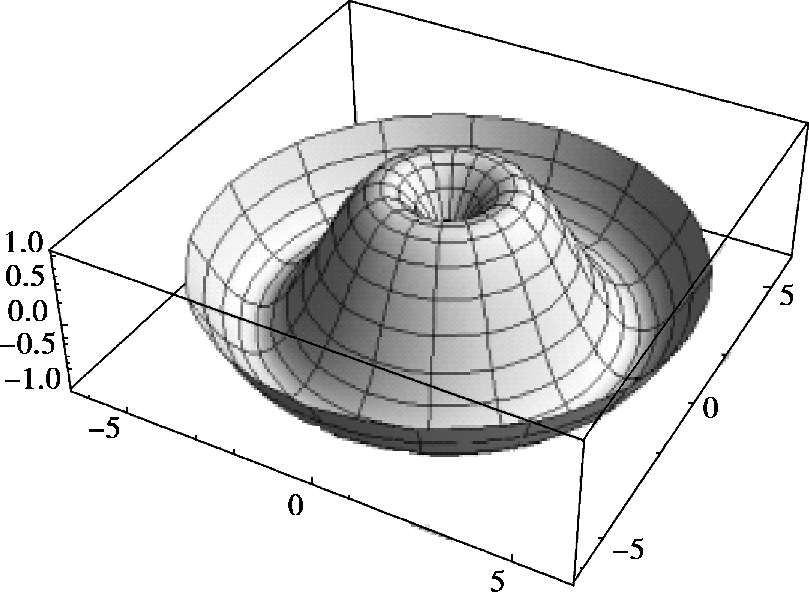
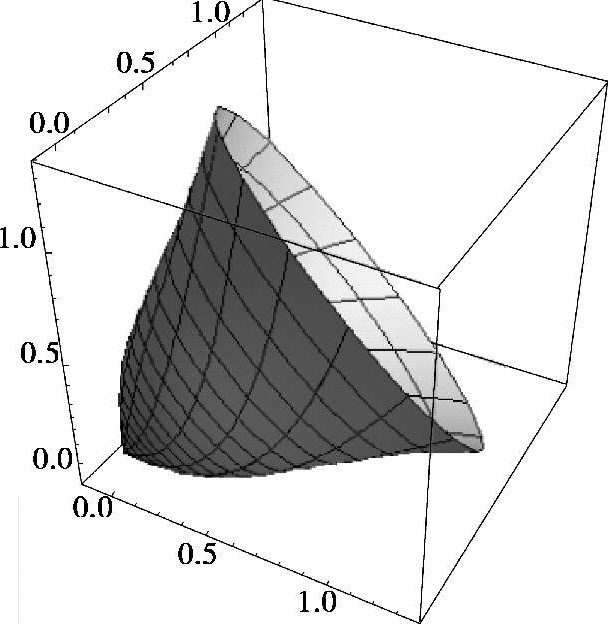
例 2.7 作曲线 z = x 3 绕起点在原点的向量{1,1,1}为轴旋转的曲面.
解 In[1]:= RevolutionPlot3D[x 3 ,{x,0,1}],RevolutionAxis➝{1,1,1}]
Out[1]=
1.求与 z 轴和点 A (1,3,-1)等距离的点的轨迹方程.
2.指出下列各点所在的卦限.
(1)(-1,-2,3);(2)(3,-2,-1);(3)(-1,3,-6).
3.已知点 A (2,3,1), B (2,0,-1):
(1)求 OA 及 AB ;(2) A 点关于 xOy 平面对称点的坐标.