




上一节介绍了如何使用整个训练数据集计算损失函数的梯度,并沿着梯度方向的反向更新模型的参数、最小化损失函数。这就是为什么这种方法有时也被称为全批梯度下降。假设有一个非常大的数据集,包含数百万个数据样本,这在许多机器学习应用中并非罕见。在这种情况下,运行全批梯度下降运算成本巨大,因为向全局最小值点每迈出一步都需要使用整个训练数据集计算梯度。
随机梯度下降(Stochastic Gradient Descent,SGD)是全批梯度下降算法的一个常用替代算法。随机梯度下降算法有时也被称为迭代梯度下降算法或在线梯度下降算法。全批梯度下降算法使用所有训练样本的累积误差总和来更新权重,即
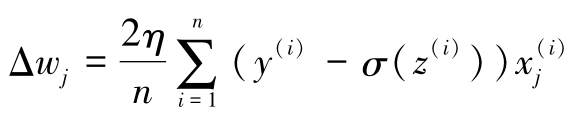
而随机梯度下降算法使用每个训练样本逐步更新权重,即
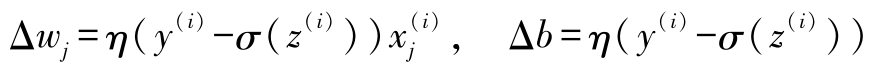
虽然随机梯度下降可以被视为梯度下降的近似,但因为随机梯度下降更频繁地更新权重,所以通常收敛更快。由于随机梯度下降算法的每个梯度都使用单个训练样本计算得到,因此相比于全批梯度下降,随机梯度下降计算的梯度噪声更大。但这也带来一个优势,即如果使用非线性损失函数,那么随机梯度下降可以更容易逃脱不太深的局部最小值。第11章将会展示随机梯度下降的这个优势。为了使随机梯度下降获得满意的结果,很重要的一点是训练样本的顺序随机,同时,在每个epoch中都要对所有训练样本随机乱序以防止每个epoch使用同样顺序的训练样本。
在训练过程中调整学习率
在随机梯度下降中,经常使用随时间变小的自适应学习率 η ,而非固定值的学习率,例如,学习率可以为如下形式:

其中 c 1 和 c 2 为常数。还要注意随机梯度下降并不能保证到达全局最小点,而是收敛到一个非常靠近全局最小点的区域。使用自适应学习率可以进一步靠近全局最小点。
随机梯度下降的另一个优点是可以在线学习。在在线学习中,随着新的训练数据产生,模型可以实时训练,这在积累大量数据的情况下尤其有用,例如,互联网应用程序中的客户数据。使用在线学习,系统可以实时适应数据的变化。另外,如果计算机存储空间有限,可以在模型更新后丢弃训练数据。
小批梯度下降
批梯度下降和随机梯度下降之间的折中即为小批梯度下降。小批梯度下降可以理解为对训练数据的较小子集采用批梯度下降,例如,每次使用32个训练样本。小批梯度下降的优点是权重更新更加频繁,算法收敛更快。此外,小批梯度下降可以使用线性代数中的向量化操作(例如,通过点积实现加权求和)取代随机梯度下降中的for循环,从而进一步提高了算法的计算效率。
由于已经使用梯度下降实现了Adaline学习规则,因此只需要对代码做一些调整让其使用随机梯度下降更新权重。在fit方法中,使用每个训练样本更新权重。此外,为了实现在线学习,增加了partial_fit方法,该方法不重新初始化权重。为了检查算法在训练后是否收敛,在每次epoch后计算所有训练样本的平均损失函数值。此外,在每次epoch开始之前,对训练数据进行乱序,以避免优化损失函数时每次epoch重复循环。通过random_state参数,允许使用随机种子来确保实验可复现。




AdalineSGD分类器使用的_shuffle方法的工作原理如下:通过调用np.random中的permutation函数产生0到100的乱序数字。然后,用这些数字作为索引对特征矩阵和类别标签向量进行乱序。
使用fit方法训练AdalineSGD分类器,并使用plot_decision_regions绘制训练结果:

运行上述代码可以获得如图2.15所示的两个图。
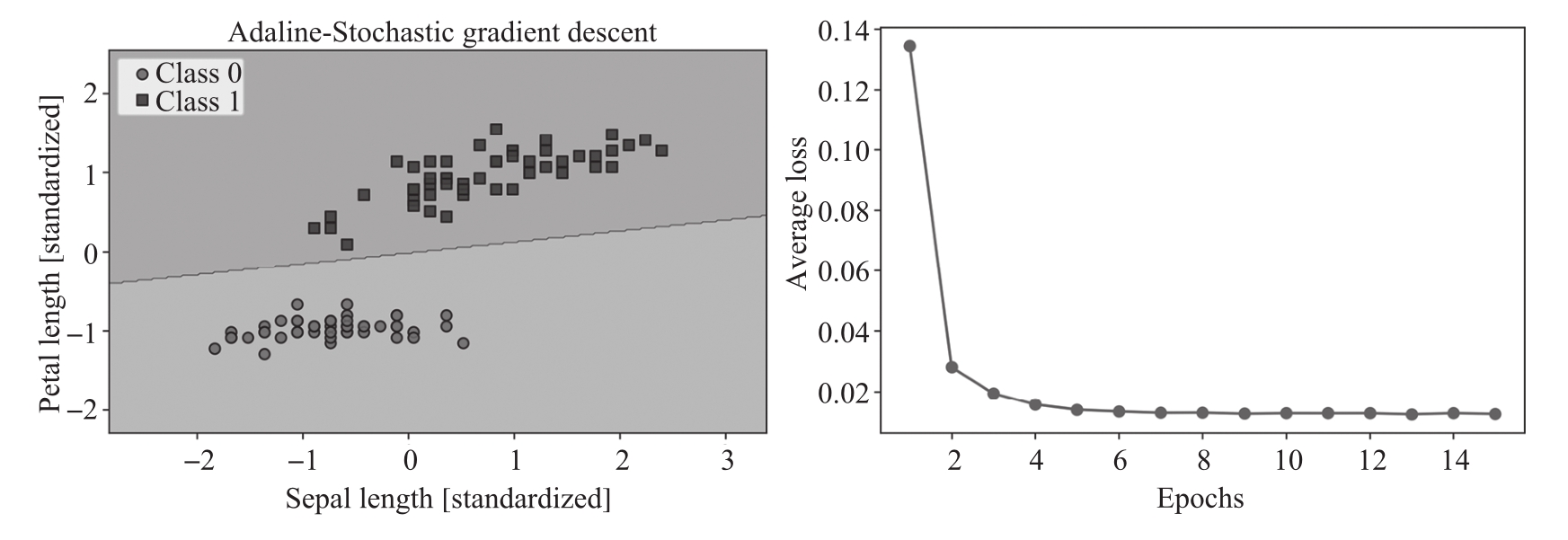
图2.15 使用SGD训练Adaline模型的决策区域和平均损失函数图
如图2.15所示,平均损失函数值下降得非常快,在15次epoch后的最终决策边界看起来与批梯度下降Adaline的结果类似。如果想更新模型,例如,实现使用流式数据的在线学习,可以在单个训练样本上调用partial_fit方法,例如ada_sgd.partial_fit(X_std[0,:],y[0])。