下载掌阅APP，畅读海量书库
立即打开
由于感知机规则和Adaline规则非常相似，因此可以使用之前实现的感知机代码，更改其fit方法，从而通过梯度下降法最小化损失函数并更新权重和偏置项：
不像感知机中那样在训练完每个样本后更新权重，Adaline使用整个训练数据集计算梯度。通过self.eta*2.0*errors.mean()完成偏置项的更新，其中errors为一个包含偏导数
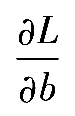的数组。用同样的方法更新权重。但请注意，更新权重需要计算偏导数
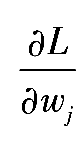，这个偏导数涉及特征值
x
j
，可以通过将errors乘以权重对应的特征值计算得到：
为了更有效地实现权重的更新，不使用for循环，而使用特征矩阵和误差向量的乘积：
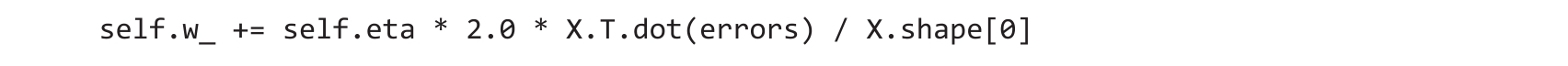
请注意，activation方法对代码没有影响，因为activation方法只是一个输出与输入相同的函数。这里，通过添加激活函数（activation方法）来说明信息通过单层神经网络传递所涉及的一般概念：输入数据的特征、净输入、激活函数、输出。
下一章将介绍使用非恒等、非线性激活函数的逻辑回归分类器。我们将看到逻辑回归模型和Adaline密切相关，唯一的区别在于激活函数和损失函数。
与之前的感知机实现类似，self.losses_列表存储损失函数值，以验证Adaline算法在训练过程中是否收敛。
矩阵乘法
矩阵乘法与向量点积非常相似，计算时把矩阵中的每一行当成一个行向量。这种向量化方法在表示时更加紧凑，从而使用NumPy计算时也更加高效，例如：
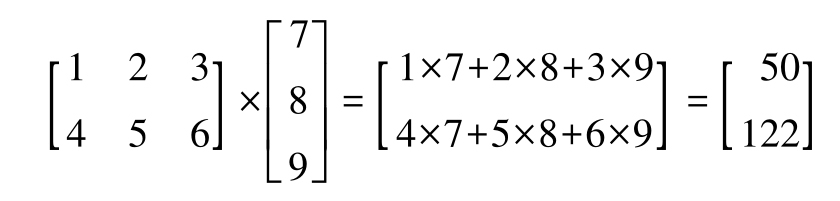
请注意，上述等式用一个矩阵右乘一个向量，数学上对此并无定义。然而，正如本书之前所述，向量可以被表示为3×1的矩阵。
在实践中，通常需要一些实验才能找到一个使算法收敛的学习率 η 。在此，选择使用两个不同的学习率，分别为 η =0.1和 η =0.0001。可以绘制损失函数与epoch次数的关系图，以便查看Adaline在训练过程中学习的情况。
超参数
学习率 η （eta）和epoch次数n_iter是感知机与Adaline学习算法的超参数（或调优参数）。第6章会介绍诸多使分类模型性能最佳的超参数寻找方法。
下述代码使用两种不同的学习率，并绘制了损失函数值与epoch次数之间的关系图：
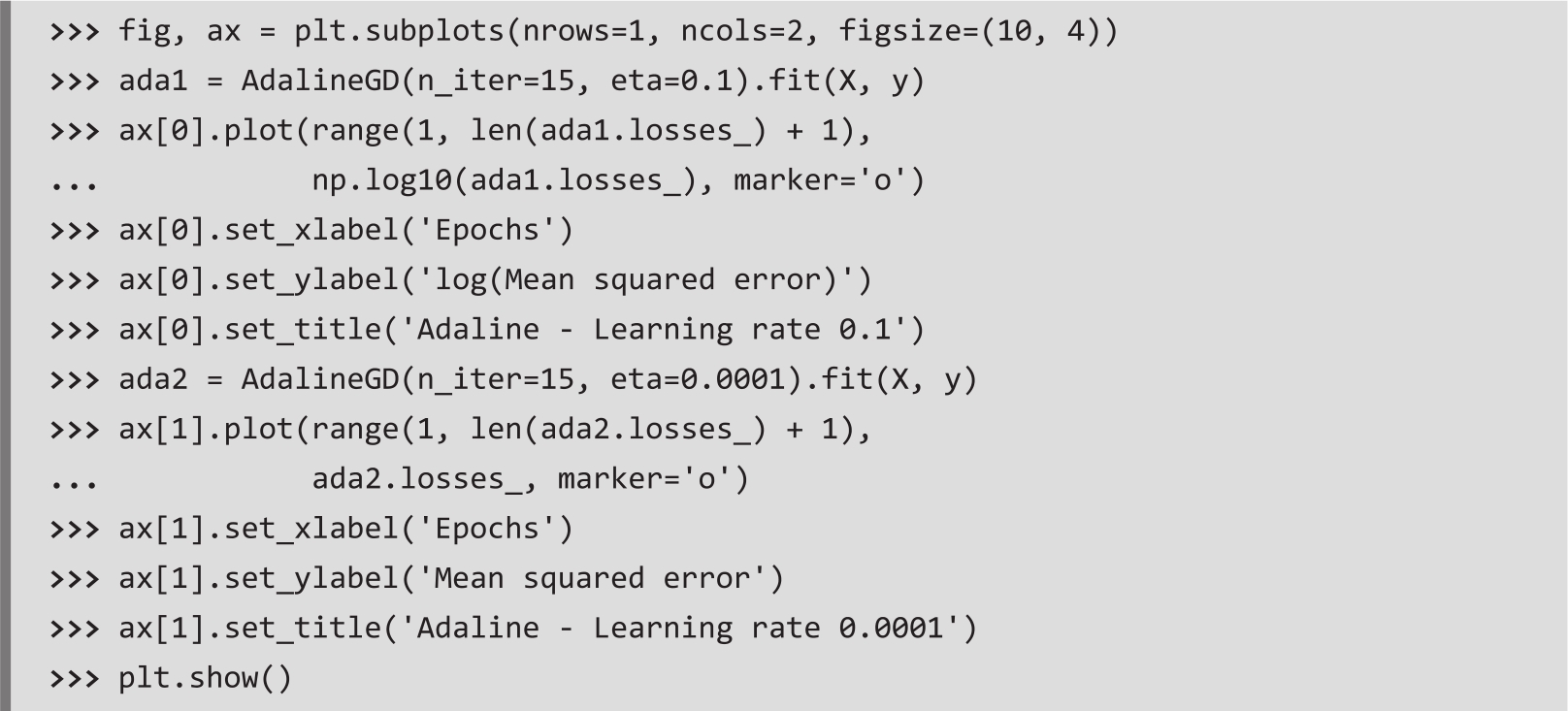
从图2.11绘制的损失函数图可以看到两个问题。左图显示了学习率太大会发生的问题。如果学习率太大，那么损失函数的全局最小值容易被跨过，以至于损失函数没有被最小化，反而均方误差MSE随着epoch次数增加不断变大。从右图可以看到损失函数在减小，但是因为学习率 η =0.0001太小，所以算法需要多次epoch才能收敛到损失函数的全局损失最小值。
图2.12说明了学习率对最小化损失函数的影响。左图显示如果选择一个好的学习率，损失函数值会逐渐减小，并朝着全局最小值的方向移动；右图显示如果选择的学习率太大，则会跨过全局最小值。
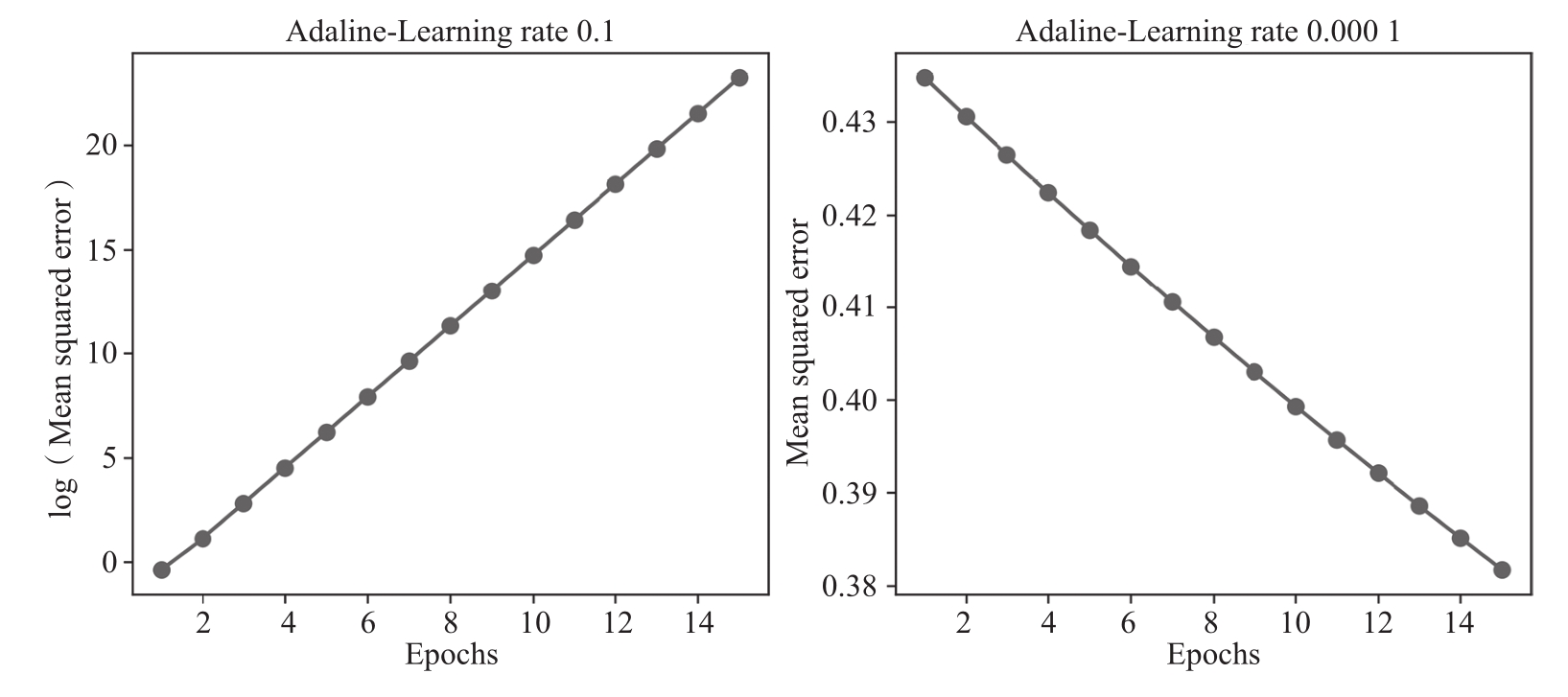
图2.11 误差与次优学习率关系图
图2.12 好的学习率和过大的学习率对梯度下降的影响