




(1) Verify the law of conservation of momentum.
(2) Understand the characteristics of incompletely elastic collision and completely inelastic collision.
(3) Master the application methods of the air track and the general computer counter.
Air track, sliding block, photoelectric door, general computer counter, nylon sticky tape, etc.

Figure 3.1.1 Air track
1—Surface of track; 2—Track; 3—Supporting feet; 4—Sliding block; 5—Pulley; 6—Air inlet
1) Air track
Air track(Figure 3.1.1) is a new mechanical experimental instrument invented in the 20th century. It is mainly composed of a 1.5 meter-long hollow track and the sliding block. There are several air holes on the smooth surface of the air track. The supporting feet installed under the track are used to adjust the level of the air track. The photoelectric gate is installed on the track to detect the corresponding time.
(1) Surface of the track: The air track is made of aluminum alloy, about 1 500 mm or 1 800 mm long, and 50 mm wide. There is a 90° included angle between the two smooth planes. Moreover,each side has two rows of 0.5 mm air holes with about 20 mm hole center distance.
(2) Track: A hollow structure made of aluminum alloy.
(3) Supporting feet: Three-point structure and adjustable screws, where one foot at one end and two feet at the other end.
(4) Sliding block: It is made of aluminum alloy and possesses a smooth inner surface, which is consistent with the rail surface. The light baffle and the spring can be respectively placed above the slide top and its two ends.
(5) Pulley: Composed of the plastic pulley and the clock pendulum needle, the pulley weighs 0.3 g can flexibly rotate.
(6) Air inlet: It is used to collect the external gas supply device.
2) Application methods and attentions
We should firstly connect the air supply, vent pipe and track, then turn on the air supply device to assure about 1 standard atmosphere gas ejection from air holes of track. In the following, the sliding block can be placed on the track and some researches can be conducted. The sliding block can be approximately used as an ideal movement body with little sliding friction, therefore, the experimental results can be almost identical to that without sliding friction. During the experiment,some attention points are in the following:
(1) Do not vibrate or weigh the air track to avoid deformation.
(2) Avoid collisions between the rail surface and the sliding block. Handle the sliding block with care to prevent falling, which may lead to damage or deformation.
(3) The rail surface and the inside surface of the sliding block should be kept dry and clean,and they should be cleaned regularly with anhydrous alcohol.
(4) During the experiment, we must first turn on the air supply device, and then put the sliding block gently on the rail surface. After finishing the experiment, we must first remove the sliding block, and then turn off the air supply device. Do not place or move the sliding block on the rail surface when no air is supplied!
(5) The compressed air into the track must be dried and filtered. Water vapor, oil and impu rities should be strictly prohibited to avoid blocking of air holes or damaging the air track.
(6) When the experiment is over, the air track should be covered with the tablecloth to pre vent dust.
(7) If the air holes are blocked, we should clean the air holes with 0.5 ~ 0.8 mm steel wire,and clean them with anhydrous alcohol.
According to the law of conservation of momentum, the total momentum of a system remains constant when the net external force on this system is zero or no external force exists in this system.It can be further concluded that the total momentum of a system in one direction is conserved when no external force acts in this direction or the net external force in this direction is zero. Moreover ,the conservation of momentum is a very useful tool for dealing with collision processes. During the collision experiment on the air track, on the one hand, the slide friction is negligible due to the floating effect of the air track. On the other hand, the air resistance can also be ignored when the speed of the object is relatively small. As a result, the collision system along the horizontal direction on the air track can be approximately regarded as a system with no external force so the total momentum before the collision is the same as that afterwards.
Assuming that the masses of the two sliding blocks are m 1 and m 2 respectively, and their veloc ities before the collision are v 10 and v 20 , and the velocities after the collision are v 1 and v 2 . According to the law of conservation of momentum:

1) Elastic recovery coefficient
The elastic recovery coefficient e is the ratio of the absolute value of relative velocity of two bodies after the collision to that before the collision, which can be expressed as:

2) Classification of collision motions
According to the elastic recovery coefficient, collision motion can be divided into the following three categories:
(1) When e is equal to 1, it is a completely elastic collision. In this case, the collision object is made up of elastic material, and the deformation after collision can be completely recovered, so the momentum and mechanical energy of such collisions are conserved.
(2) When 0 < e < 1, it is an incompletely elastic collision. In this case, the collision object has certain plasticity and the deformation after collision cannot be completely recovered. Moreover,the lost kinetic energy can be transformed into other types of energy, such as thermal or potential energy. Therefore, the total momentum of such collisions is conserved, but the mechanical energy is not.
(3) When e is equal to 0, it is called a completely inelastic collision. In this case, the two objects stick together and move at the same speed as the result of the collision, so the momentum of such collision is conserved, but there will be more lost mechanical energy of the object.
3) Verification of the law of conservation of momentum by the incomplete elastic collision
During the experiment, two sliding blocks with the mass of m 1 and m 2 ( m 1 > m 2 ) are used and the sliding block 2 (the smaller one) is put between the two photoelectric gates, where v 20 = 0, and then we push the sliding block 1 (the bigger one) with the velocity v 10 to collide the sliding block 2. After the collision, the velocities of the two sliding blocks become v 1 and v 2 respectively. According to the law of conservation of momentum:

The kinetic energy changes before and after collision can be expressed as:
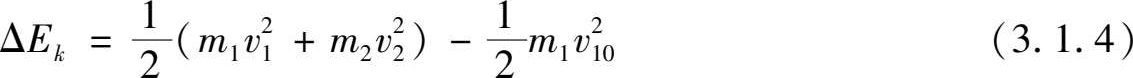
According to Equation (3.1.3) and Equation (3.1.4), as long as the masses of the two sliding blocks, the velocities v 10 , v 1 , v 2 of the sliding blocks before and after the collision are measured, the conservation of momentum can be verified and then the change of kinetic energy before and after the incomplete elastic collision can be calculated.
During the actual moving process, the sliding blocks will move at a certain acceleration over the “leveling” air track. The reason can be interpreted in the following: on the one hand, the air resistance can introduce the damping effect at a certain extent. One the other hand, it is very difficult to absolutely level the track. Also, a little bend on the track can exist. Therefore, the difference between the speed measured by the photoelectric door and the actual movement speed is inevitable and the corresponding speed correction must be conducted.
According to Figure 3.1.2, the three accelerations can be measured and the corresponding velocity can be corrected. In Figure 3.1.2, two sliding blocks are placed at the collision positions C and D, which are respectively corresponding to the center position of the light block of the two sliding blocks. A and B are in the actual measurement position for the sliding block speed during the experiment.

Figure 3.1.2 Schematic diagram of velocity correction
(1) Assuming that the distance between A and C is s 10 , and the velocity of the big sliding block 1 passing through door A is measured as v 1A , and then move door B to position C while keeping door A motionless, the acceleration of the sliding block 1 between A and C is measured as a 10 . It can be expressed as:

(2) Assuming that the distance between B and C is s 1 , and the velocity of the big sliding block 1 passing through door B is measured as v 1B , and then move door B back to position B, and move door A to position C, and the acceleration of sliding block 1 between C and B is measured as a 1 . It can be expressed as:

(3) Assuming that the distance between D and B is s 2 , and the velocity of the small sliding block 2 passing through door B is measured as v 2B , and then move door A to position D while keeping door B motionless, and the acceleration of sliding block 2 between D and B is measured as a 2 .It can be expressed as:

4) Verification of the law of conservation of momentum by the complete inelastic collision
When a completely inelastic collision occurs between two objects, the elastic recovery coefficient e = 0. We place the sliding block 2 between the photoelectric gate A and B, and v 20 = 0,and then the sliding block 1 collides with the sliding block 2 with the velocity v 10 . After the colli sion, the two sliding blocks stick together and move at the same velocity v 2 . According to the mo mentum conservation formula, it can be expressed as:

The energy loss during the collision is
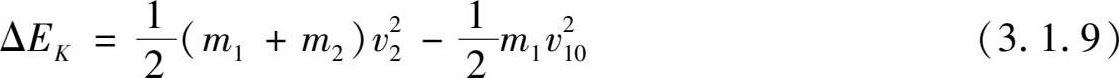
The corrections of velocity v 10 and v 2 are similar to that in Figure 3.1.2.
1) Flatten the air track
Turn on the gas supply device and place a sliding block on air track, and then the leveling state can be judged according to the state of the sliding block.
(1) Judging in the stationary state: when the air track is leveling, the sliding block can be stabilized at any position on the track.
(2) Judging in the state of motion: when the sliding block moves on the air track, the velocity remains unchanged or the acceleration is zero.
2) Incomplete elastic collision experiment
(1) Preparation: The photoelectric gates are fixed at A and B positions about 40 cm apart.The function of the computer counter is set to measure the speed, and the unit is also converted to the speed unit accordingly. Check the states of the light baffle and spring of the sliding block to ensure that the light baffle is valid and the head-on collision occurs when the sliding block passes through the photoelectric gate.
(2) Select the collision location: Place the sliding block 1 and 2 between doors A and B, as is shown in Figure 3.1.2 (the springs of the two sliding blocks just touch each other, and the small sliding block is on the side of door B), and then record the central positions of the two sliding blocks, namely positions C and D.
(3) Measure v 1A , v 2B and v 1B : Place the small sliding block 2 in position D and make it motionless ( v 20 = 0), gently push the large sliding block 1 to the back spring equipped in the rear end of the track, which can bounce the sliding block 1 back to collide the sliding block 2, and then record the corresponding velocities before and after the collision.
(4) Velocity correction: Referring to Figure 3.1.2, the values of a 10 , a 1 and a 2 can be measured respectively. When we measure the acceleration, the velocity of the sliding block should be almost equal to that at the time of collision. Especially, in order to reduce the measurement error, the measurement should be repeated about 3 ~ 5 times to get the average value.
3) Complete inelastic collision experiment
The collision surfaces of the two sliding blocks should be placed with nylon tape for collision and the spring is removed, and make sure v 20 = 0. Then the experimental observation and data recording methods are similar to that in content 2).
1) Record of experimental data
Record your observations in Table 3.1.1 and Table 3.1.2, respectively.
Table 3.1.1 Record table for incompletely elastic collision experiment

Table 3.1.2 Record table for completely inelastic collision experiment

2) Experimental data processing
(1) Judge whether the momentum and mechanical energy are conserved through calculating the variations of momentum and kinetic energy before and after the collision for the two types of collisions.
(2) Calculate the elastic recovery coefficient e for two types of collisions.
(3) Analyze and evaluate the experimental results.
(1) How does the photoelectric gate measure velocity and acceleration?
(2) Why the large sliding block is used to collide with small sliding block in the incompletely elastic collision experiment?
(3) What measurements can be adopted to reduce the experimental errors?