




Significant figures are closely related to that of the measurement error. Since measurement error is inevitable, both observations and measurements are approximations. Significant figures are to indicate how reliable the approximations are. The measured values are usually estimated to a few tenths of the minimum scale of the measuring apparatus in one measurement. Thus, error exists in the last digit of a measured value, which is called doubtful figures. The other figures on top of the doubtful figures are accurate, which are called reliable figures, say for reliable figures, together with the last digit of relevant doubtful figures, constitute the significant figures.
The digits of significant figures of an approximation can roughly indicate the magnitude of relative error. Forexample,the relative error of the approximate value 0.023 7 m is
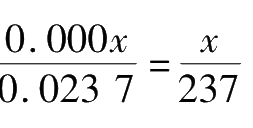 (
x
is the error of the last digit of the significant figures), the relative error of the approximate value 312.0 cm is 0.
x
/312.0 =
x
/3 120. Generally speaking, the relative errors of an approximation with one, two, three … digits of significant figures are
x /
10 ~
x /
100,
x /
100 ~
x /
1 000 …. respectively. Therefore, the number of significant digits indicates the magnitude of the error.
(
x
is the error of the last digit of the significant figures), the relative error of the approximate value 312.0 cm is 0.
x
/312.0 =
x
/3 120. Generally speaking, the relative errors of an approximation with one, two, three … digits of significant figures are
x /
10 ~
x /
100,
x /
100 ~
x /
1 000 …. respectively. Therefore, the number of significant digits indicates the magnitude of the error.
As the digit of the significant figures of the approximate value is related to the magnitude of the error, the digit will not change when the unit changes. For example, 0.027 3 m can be written as 2.73 cm or 0.000 027 3 km. They both are 3-digit significant figures with a doubtful figure in the last digit. However, the approximation can not be written as 27 300 μm because it is a 5-digit significant figure. Instead, it should be written as 2.73 × 10 4 μm as the scientific notation. The proper format for scientific notation is ( a times 10 to the power of b ) to put a as a number or decimal number which conform to 1 ≤| a |< 10, and b is the power of 10 required so that the scientific nota tion is mathematically equivalent to the original number.
The number of significant digits of a measured or calculated value should be recorded based on the absolute error (usually take one significant digit). The order of magnitude of the last digit of the result should be consistent with that of the error. For example, the average of multiple measurements of a length comes at 68.583 cm, and the calculation reveals that the absolute error is 0.2 cm,then the average value should be 68.6 cm, leaving the result denoted as (68.6 ± 0.2) cm. The error is reflected in the last digit of the result.
(1) While conducting addition or subtraction, the digits of significant figures in the decimal portions are only brought into consideration. The result should have no more significant decimal dig its than the least number of digits counted earlier. For others with more decimal digits, rounding them off is always acceptable. Take one more decimal digit for calculation, and round off the final result according to the standard significant digits. For example, 1.2345 + 3.456 -4.18 + 13.2≈13.7.
(2) While conducting multiplication or division, the least digit of significant figures (considering the number as a whole, not just the decimal portion) determines the digit of significant figures in an answer. Round the others with more significant digits off. Take one more digit for calculation then round off the final result based on the standard significant digits.For example,
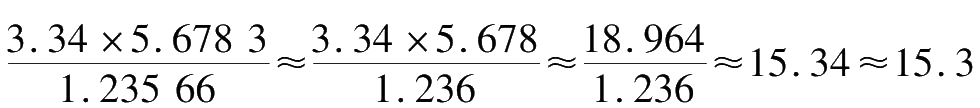 .
.
(3) While conducting exponentiation, extraction of root, logarithm operation and others, the digit of final result should be consistent with that of the original value. For example,
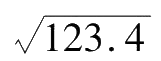 ≈11.11,3.12
2
≈9.92, log 12.34≈1.091.
≈11.11,3.12
2
≈9.92, log 12.34≈1.091.
(4) The digit of constants (π,
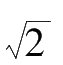 , etc. ) and intermediate results can be determined by following rules: take one more digit for calculation, and round off the final result according to the standard significant digit. The best way to implement the method of Banker’s Rounding. When the last digit stands more than 5, round it up to the nearest integer. If it stands less than 5, round it down no doubt. If the last digit stands at 5 precisely, round it up towards the nearest even integer.
, etc. ) and intermediate results can be determined by following rules: take one more digit for calculation, and round off the final result according to the standard significant digit. The best way to implement the method of Banker’s Rounding. When the last digit stands more than 5, round it up to the nearest integer. If it stands less than 5, round it down no doubt. If the last digit stands at 5 precisely, round it up towards the nearest even integer.