




1.设M是{1,2,…,15}的一个子集,且M中任意3个元素的乘积都不是完全平方数,求|M|的最大可能值。
2.给定有限非空集合A,定义P(A)为A的所有子集组成的集合。设f:P(A)→P(A)满足:若X⊆Y,则f(X)⊆f(Y)。证明:存在A的一个子集T满足f(T)=T。
3.设S={1,2,…,100},求满足下列条件的最大正整数n:存在S的n个两两不同的子集,使得对于任意两个子集,若它们的交集非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同。
4.取出{1,2,…,2021}的一些子集,使得任意两个被取出的子集的交集都含有3个连续的正整数,求取出的子集数目的最大值。
5.设n是一个大于1的奇数,A 1 ,A 2 ,…,A n 是两两不同的集合,考虑集合T={A i ΔA j |1≤i<j≤n}。证明:|T|≥n。
6.给定正整数n,设A 1 ,…,A k ,B 1 ,…,B l 是一些有限数集(可以有空集),且满足:
(1)A 1 ,…,A k 中任意两个集合不同,B 1 ,…,B l 中任意两个集合不同;
(2)k+l>2 n 。
设S={X|∃1≤i≤k,1≤j≤l,使得X⊆A i ∪B j },求|S|的最小可能值。
7.对于非空数集S,T,定义S+T={s+t|s∈S,t∈T},2S={2s|s∈S}。设n为正整数,A,B是{1,2,…,n}的非空子集,证明:存在A+B的子集D,使得D+D⊆2(A+B),且
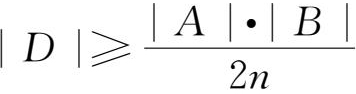 。
。
8.求所有整数n≥3,使得存在n元集S的三元子集族F满足以下两个条件:
(1)对S中任意两个不同元素a,b,F中恰存在一个集合同时包含a,b;
(2)对S中任意六个不同元素a,b,c,x,y,z,若{a,b,x},{b,c,y}和{c,a,z}都在F中,则{x,y,z}在F中。
1.在一个2021×2021的方格表中,每个格子均被染成黑色或白色之一,下面可以进行如下操作:选取一个3×3或4×4的小正方形,将其内部的9个或16个方格颜色全部改变(黑变白,白变黑)称为一次操作。请问,是否不论初始条件如何,都一定能通过若干次操作,使得所有方格都变白?
2.给定正整数k,甲乙两人轮流在9×9的方格表中填数,甲每次可以选择一个空方格填入0,乙每次可以选择k个空方格并依次填入1。若在操作的过程中出现每行每列的所有数之和都是奇数,则乙获胜,若所有格子都被填入数之后此状态还未出现,则甲获胜。求最小的正整数k,使得乙有必胜策略。
3.求最小的正整数n,使得可以将25×25的棋盘n染色并满足:任取一个不是最右边一列也不是最上面一行的格子A,在A的正上方任取一个格子B,在A的正右方任取一个格子C,均有A,B,C不全同色。
4.一个N×N的方格表的每个格都填有一个0,现可进行如下操作:擦去某行或某列的所有数字,然后将1,2,…,N按任意顺序填入这些格中。经过有限次操作后,求所有方格中数字之和的最大可能值。
5.求所有的正整数n,使得存在正整数N,a,b(a≠b)满足下列条件:可以将N×N的正方形分成n个a×b或b×a的矩形,且两种矩形都要出现。
6.有一百万头牛分别位于1000×1000网格的各个格子中,每格里一头牛。将该网格的左右两边粘在一起,上下两边也粘在一起。有些牛是诚实的,总是说实话;而其余的牛是不诚实的,从不说实话。这一百万头牛中的每头牛均宣称:与我相邻的牛中至多有一头是诚实的。我们称一对相邻的牛为“牛仔对”,如果其中恰有一头牛是诚实的。求此网格中牛仔对的最小可能值。
注:如果两头牛所在的网格(x 1 ,y 1 ),(x 2 ,y 2 )满足如下条件:x 1 =x 2 且y 1 -y 2 ≡±1(mod1000),或者x 1 -x 2 ≡±1(mod1000)且y 1 =y 2 ,则称它们是“相邻”的。
7.证明:存在正整数N满足对任意正整数n>N,若将一个n×n的方格表用n种颜色染色,每种颜色染n个方格,则存在一个边长为
 且边平行于方格表的边的正方形,它至少包含4种颜色的完整方格。
且边平行于方格表的边的正方形,它至少包含4种颜色的完整方格。
8.坐标平面上每个横纵坐标是整数的点都被染成了1201种颜色之一。已知对任意两点(x 1 ,y 1 )与(x 2 ,y 2 ),若|x 1 -x 2 |+|y 1 -y 2 |≤48,则它们颜色不同。证明:对任意两点(x 1 ,y 1 )与(x 2 ,y 2 ),若它们的一个坐标相同,另一个坐标之差(大减小)小于1201,则它们的颜色不同。