




1.平面上3000条直线,任意两条都不平行,任意三条都不共点,求证:这些直线将平面分成的区域中,至少有2000块是三角形。
2.一次比赛的所有选手中,有些人互相认识。已知存在整数k≥2满足:所有选手可以分成k组,使得每组中的任意两名选手都不认识,但不可按同样的要求分成k-1组。证明:可以将所有选手分成k组(记为A 1 ,A 2 ,…,A k ),使得每组中的任意两名选手不认识,并选择选手c i ∈A i (i=1,2,…,k),使得c i 与c i +1认识(i=1,2,…,k-1)。
3.设G是一个有2021个顶点的简单图,对每个顶点v,定义f(v)为满足下列条件的最大正整数n:存在v的n个邻居,这些邻居两两不相邻。求所有f(v)之和的最大可能值。
4.100×100的方格表的每一格内有一只蜜蜂,在某一时刻它们全部飞起并各自降落在方格表的某个格子中(允许同一个格子内落多只蜜蜂,也允许某些蜜蜂不动)。已知对于任意两只起飞前在相邻(这里的相邻指具有公共边或公共顶点)格子中的蜜蜂,它们或者落在同一个格子中,或者落在相邻的两个格子中。试证明:一定有一只蜜蜂,它或者没有移动,或者飞到了其所在格子的某相邻格子中。
5.整数n,k满足n≥k≥3。某个年级有2n名学生,其中每名学生恰有k个朋友(朋友是相互的)。证明:可以将这些学生分成两个班,每个班有n名学生,且每名学生在他自己的班级里至少有一个朋友。
6.设k是一个大于1的整数,S是一个k元集合,f
1
,f
2
,…,f
k
是S→
R
的映射。对于1≤n≤k,定义由S的两两不同的元素组成的序列(A
1
,A
2
,…,A
n
)是一个“n-好的”序列,若对任意由S的两两不同的元素组成的序列(B
1
,B
2
,…,B
n
),都有
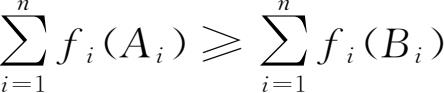 。
。
设(A 1 ,A 2 ,…,A m )是一个“m-好的”序列,其中1≤m≤k-1,证明:存在一个“(m+1)-好的”序列(C 1 ,C 2 ,…,C m+1 )满足{A 1 ,A 2 ,…,A m }⊆{C 1 ,C 2 ,…,C m+1 }。
7.给定正整数n,选出集合{1,2,…,n}的一些子集,已知这些子集满足下列性质:任意两个子集最少有2个公共元素,任意3个子集最多有3个公共元素。证明:选出的子集不超过100n 2 个。
8.一个n阶完全图被拆成了n个小完全图,每个小完全图的点数均不小于3。证明:这些小完全图的点数均相同。