下载掌阅APP，畅读海量书库
立即打开
1．求证：多项式x
6
-x
5
+x
4
-x
3
+x
2
-x+
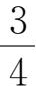没有实根。
2．设a,b,c∈ R 使得方程x 3 +ax 2 +bx+c=0有3个实根。证明：若-2≤a+b+c≤0，则至少存在一个根在区间[0,2]中。
3．设非负实数a,b,c满足a+b+c=1，求证：9abc≤ab+bc+ca≤
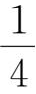(1+9abc)。
4．已知
+
+
+
+
+
=
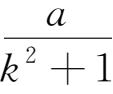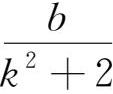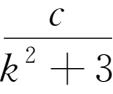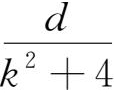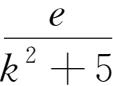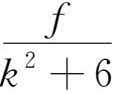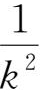对k=1,2,3,4,5,6均成立，求a+b+c+d+e+f的值。
5．设n次多项式f(k)=
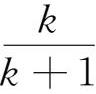(k=0,1,…,n)，求f(n+1)。
6．求最大的实数λ，使得当实系数多项式f(x)=x 3 +ax 2 +bx+c的所有根都是非负实数时，只要x ≥0，就有f(x)≥λ(x-a) 3 ，并求式中等号何时成立。
7．求所有的实系数多项式对(P(x),Q(x))，使得对无穷多个x ∈ R ，有
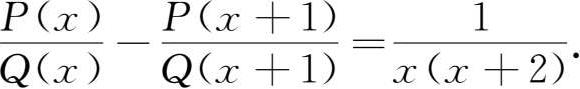
8．n×n矩阵中，第i行第j列的元素等于a i +b j ，这里a 1 ,a 2 ,…,a n ,b 1 ,b 2 ,…,b n 都是给定的实数；矩阵每一行数的乘积都是相等的。证明：每一列数的乘积都是相等的。
9．设ε
k
=cos
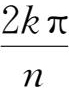+isin
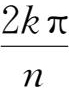(k=0,1,2,…,n-1)，求值：ε
k
·
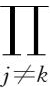ε
k
-ε
j
。
10．设多项式P(x)=x
n
+a
1
x
n-
1
+…+a
n-1
x+a
n
有复根x
1
,x
2
,…,x
n
,α=
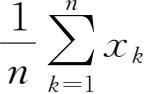,β
2
=
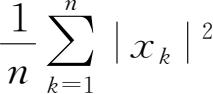，且β
2
<1+|α|
2
。若复数x
0
满足|α-x
0
2<1-β
2
+|α|
2
，求证：|P x
0
|<1。
11．设ζ≠1是复数，ζ
23
=1。计算：
。
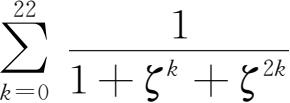