肖磊知道利用计算机技术可以采集、存储和处理各种信息,也可将这些信息转换成人类可以识别的文字、声音或视频进行输出。然而让肖磊疑惑的是,这些信息在计算机内部又是如何表示的呢?该如何对信息进行量化呢?肖磊认为,只有学习好这方面的知识,才能更好地使用计算机。
本任务要求了解计算机中的数据及其单位,了解数制及其转换、二进制数的运算、计算机中字符的编码规则和多媒体技术的相关知识。
在计算机中,各种信息都是以数据的形式呈现的。数据经过处理后产生的结果为信息,因此数据是计算机中信息的载体。数据本身并没有意义,只有经过处理和描述,才有实际意义。例如,单独一个数据“32℃”并没有什么实际意义,但将其描述为“今天的气温是32℃”时,这条信息就有意义了。
计算机中处理的数据可分为数值数据和非数值数据(如字母、汉字和图形等)两大类。无论什么类型的数据,在计算机内部都是以二进制码的形式存储和运算的。计算机在与外部“交流”时会采用人们熟悉和便于阅读的形式,如十进制数据、文字和图形等,它们之间的转换由计算机系统来完成。
计算机存储和运算数据时,通常要涉及以下3种数据单位。
数制是指用一组固定的数字符号和统一的规则来表示数值的方法。其中,按照进位方式计数的数制称为进位计数制。在日常生活中,人们习惯用的进位计数制是十进制,而计算机则使用二进制。除此以外,进位计数制还包括八进制和十六进制等。顾名思义,二进制就是“逢二进一”的数制;以此类推,十进制就是“逢十进一”,八进制就是“逢八进一”等。

计算机中常用的几种进位数制的表示
在进位计数制中,每个数码的数值大小不仅取决于数码本身,还取决于该数码在数中的位置。如十进制数828.41,整数部分的第1个数码“8”处在百位,表示800;第2个数码“2”处在十位,表示20;第3个数码“8”处在个位,表示8;小数点后第1个数码“4”处在十分位,表示0.4;小数点后第2个数码“1”处在百分位,表示0.01。也就是说,同一数码处在不同位置所代表的数值是不同的。数码在一个数中的位置称为数制的数位,数制中数码的个数称为数制的基数,十进制数有0、1、2、3、4、5、6、7、8、9共10个数码,其基数为10。每个数位上的数码符号代表的数值等于该数位上的数码乘一个固定值,该固定值称为数制的位权数。数码所在的数位不同,其位权数也不同。
无论在何种进位计数制中,数值都可写成按位权展开的形式,如十进制数828.41可写成
828.41=8×100+2×10+8×1+4×0.1+1×0.01 (1-1)
或者
828.41=8×10 2 +2×10 1 +8×10 0 +4×10 -1 +1×10 -2 (1-2)

常用数制对照关系表
式(1-1)和式(1-2)为将数值按位权展开的表达式,其中10 i 称为十进制数的位权数,其基数为10。使用不同的基数,可得到不同的进位计数制。假设 R 表示基数,则进位计数制为 R 进制,可使用 R 个基本的数码, R i 就是位权,其加法运算规则是“逢 R 进一”。任意一个 R 进制数 D 均可以展开表示为

式(1-3)中的 K i 为第 i 位的系数; i 的取值范围是[- m , n -1]( m 是小数部分的位数, n 是整数部分的位数); R i 表示第 i 位的权。
在计算机中,可以用括号加数制基数下标的方式来表示不同数制的数。例如,(492)10表示十进制数,(1001.1) 2 表示二进制数,(4A9E) 16 表示十六进制数;也可以用带有字母的形式分别将其表示为(492) D 、(1001.1) B 和(4A9E) H 。在程序设计中,常在数字后直接加英文字母来区分不同的进制数,如492D、1001.1B等。
下面将具体介绍4种常用数制相互转换的方法。
将二进制数、八进制数和十六进制数转换成十进制数时,只需用该数制的各个位数乘各自对应的位权数,然后将乘积相加,用按位权展开的方法即可得到对应的结果。
(1)将二进制数10110转换成十进制数
先将二进制数10110按位权展开,然后将乘积相加,转换过程如下所示:
(10110) 2 =(1×2 4 +0×2 3 +1×2 2 +1×2 1 +0×2 0 ) 10
=(16+4+2) 10
=(22) 10
(2)将八进制数232转换成十进制数
先将八进制数232按位权展开,然后将乘积相加,转换过程如下所示:
(232) 8 =(2×8 2 +3×8 1 +2×8 0 ) 10
=(128+24+2) 10
=(154) 10
(3)将十六进制数232转换成十进制数
先将十六进制数232按位权展开,然后将乘积相加,转换过程如下所示:
(232) 16 =(2×16 2 +3×16 1 +2×16 0 ) 10
=(512+48+2) 10
=(562) 10
将十进制数转换成二进制数、八进制数和十六进制数时,可先将数值分成整数和小数部分,然后分别进行转换,再拼接起来。
例如,将十进制数转换成二进制数时,对整数部分和小数部分分别进行转换。整数部分采用“除2取余倒读”法,即将该十进制数除以2,得到一个商和余数
K
0
;再用商除以2,又得到一个新的商和余数
K
1
;如此反复,直到商为0时得到余数
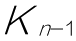 ;将各次得到的余数,以最后一次的余数为最高位、第一次的余数为最低位依次排列,即
;将各次得到的余数,以最后一次的余数为最高位、第一次的余数为最低位依次排列,即
 …
K
1
K
0
,这就是该十进制数对应的二进制数的整数部分。
…
K
1
K
0
,这就是该十进制数对应的二进制数的整数部分。
小数部分采用“乘2取整正读”法,即将十进制数的小数乘2,取乘积中的整数部分作为相应二进制数小数点后的最高位 K −1 ;取乘积中的小数部分反复乘2,逐次得到 K −2 , K −3 ,…, K −m ,直到乘积的小数部分为0或位数达到所需的精确度要求为止;然后把每次乘积所得的整数部分从小数点后自左往右依次排列( K -1 K −2 … K −m ),即所求二进制数的小数部分。
同理,将十进制数转换成八进制数时,整数部分“除8取余”,小数部分“乘8取整”;将十进制数转换成十六进制数时,整数部分“除16取余”,小数部分“乘16取整”。
提示 在进行小数部分的转换时,有些十进制小数不能转换为有限位的二进制小数,此时只能用近似值表示。例如,(0.57) 10 不能用有限位的二进制小数表示,如果要求保留5位小数,则(0.57) 10 ≈(0.10010) 2 。
例如,将十进制数225.625转换成二进制数。用“除2取余倒读”法对整数部分进行转换,再用“乘2取整正读”法对小数部分进行转换,转换过程如下所示:
(225.625) 10 =(11100001.101) 2

(1)二进制数转换成八进制数
二进制数转换成八进制数的转换原则是“3位分一组”,即以小数点为界,整数部分从右向左每3位分为一组;若最后一组不足3位,则在最高位前面添0补足3位;然后将每组中的二进制数按权相加,得到对应的八进制数。小数部分从左向右每3位分为一组;最后一组不足3位时,尾部添0补足3位;然后按照顺序写出每组二进制数对应的八进制数。
将二进制数1101001.101转换为八进制数,转换过程如下所示:

得到的结果为:(1101001.101) 2 =(151.5) 8
(2)二进制数转换成十六进制数
二进制数转换成十六进制数的转换原则是“4位分一组”,即以小数点为界,整数部分从右向左、小数部分从左向右每4位分为一组,不足4位时添0补齐。
将二进制数10111001100011.1011转换为十六进制数,转换过程如下所示:
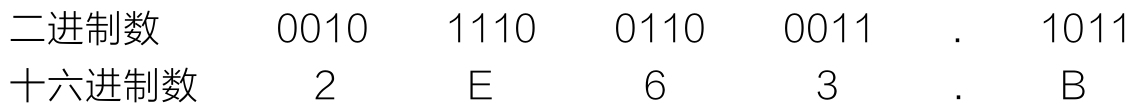
得到的结果为:(10111001100011.1011) 2 =(2E63.B)16
(1)八进制数转换成二进制数
八进制数转换成二进制数的转换原则是“一分为三”,即从八进制数的低位开始,将每一位上的八进制数写成对应的3位二进制数;如有小数部分,则从小数点开始,按上述方法分别向左右两边进行转换。
将八进制数162.4转换为二进制数,转换过程如下所示:

得到的结果为:(162.4) 8 =(1110010.1) 2
(2)十六进制数转换成二进制数
十六进制数转换成二进制数的转换原则是“一分为四”,即把每一位上的十六进制数写成对应的4位二进制数。
将十六进制数3B7D转换为二进制数,转换过程如下所示:

得到的结果为:(3B7D) 16 =(11101101111101) 2
计算机内部采用二进制数表示数据,主要原因是其技术实现简单,易于转换。二进制数的运算规则简单,可以方便地用于逻辑代数分析以及用于设计计算机的逻辑电路等。下面将对二进制数的算术运算和逻辑运算进行简要介绍。
二进制数的算术运算也就是通常所说的四则运算——加、减、乘、除,运算规则比较简单,具体介绍如下。
计算机采用的二进制数1和0可以代表逻辑运算中的“真”与“假”、“是”与“否”和“有”与“无”。二进制数的逻辑运算包括“与”“或”“非”“异或”4种,具体介绍如下。
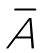 。其运算规则为:
。其运算规则为:
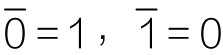 。例如,
A
变量表示男性,
。例如,
A
变量表示男性,
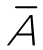 就表示非男性,即女性。
就表示非男性,即女性。
编码就是利用计算机中的0和1两个数码的不同长度表示不同信息的一种约定方式。由于计算机是以二进制编码的形式存储和处理数据的,因此只能识别二进制编码信息。数字、字母、符号、汉字、语音和图形等非数值信息都要用特定规则进行二进制编码后才能存储在计算机中。西文与中文字符由于形式不同,使用的编码方式也不同。
计算机通常采用ASCII和Unicode两种编码方式对字符进行编码。

标准7位ASCII
在计算机中,汉字信息的传播和交换必须基于统一的编码标准才不会造成混乱和差错。因此,计算机能够处理的汉字是包含在国家或国际组织制定的汉字字符集中的汉字,常用的汉字字符集包括GB 2312—1980、GB 18030—2000、GBK和CJK编码等。为了使每个汉字有统一的代码,我国颁布了汉字编码的国家标准,即GB 2312—1980《信息交换用汉字编码字符集 基本集》。这个字符集是目前我国所有汉字系统的统一标准。
汉字的编码方式主要有以下4种。
多媒体(Multimedia)是由单媒体复合而成(融合了两种或两种以上)的人机交互式信息交流和传播媒体。多媒体不仅包含文字、图形、图像、视频、音频和动画等媒体信息本身,还包含处理和应用这些媒体信息的一整套技术,即多媒体技术。多媒体技术是指能够同时获取、处理、编辑、存储和演示两种及以上不同类型的媒体信息的媒体技术。在计算机领域,多媒体技术就是用计算机实时、综合处理图像、文字、声频、音频等信息的技术,这些信息在计算机内都是被转换成由0和1表示的数字化信息进行处理的。
微课1-3

多媒体技术在工作和生活中的应用
多媒体技术主要具有以下5个特点。
多媒体计算机的硬件除了计算机的常规硬件外,还包括音频/视频处理器、多种媒体输入/输出设备、信号转换装置、通信传输设备及接口装置等。具体来说,多媒体计算机的硬件主要包括以下3类。
微课1-4

多媒体计算机的硬件
多媒体计算机的软件种类较多,根据功能的不同可以分为多媒体操作系统、多媒体处理系统工具和用户应用软件3种。
在计算机中,利用多媒体技术可以对音频、图像、视频等多种媒体信息进行综合式交互处理,并以不同的多媒体文件格式进行存储。下面介绍常用的多媒体文件格式。
微课1-5

常见的多媒体文件格式
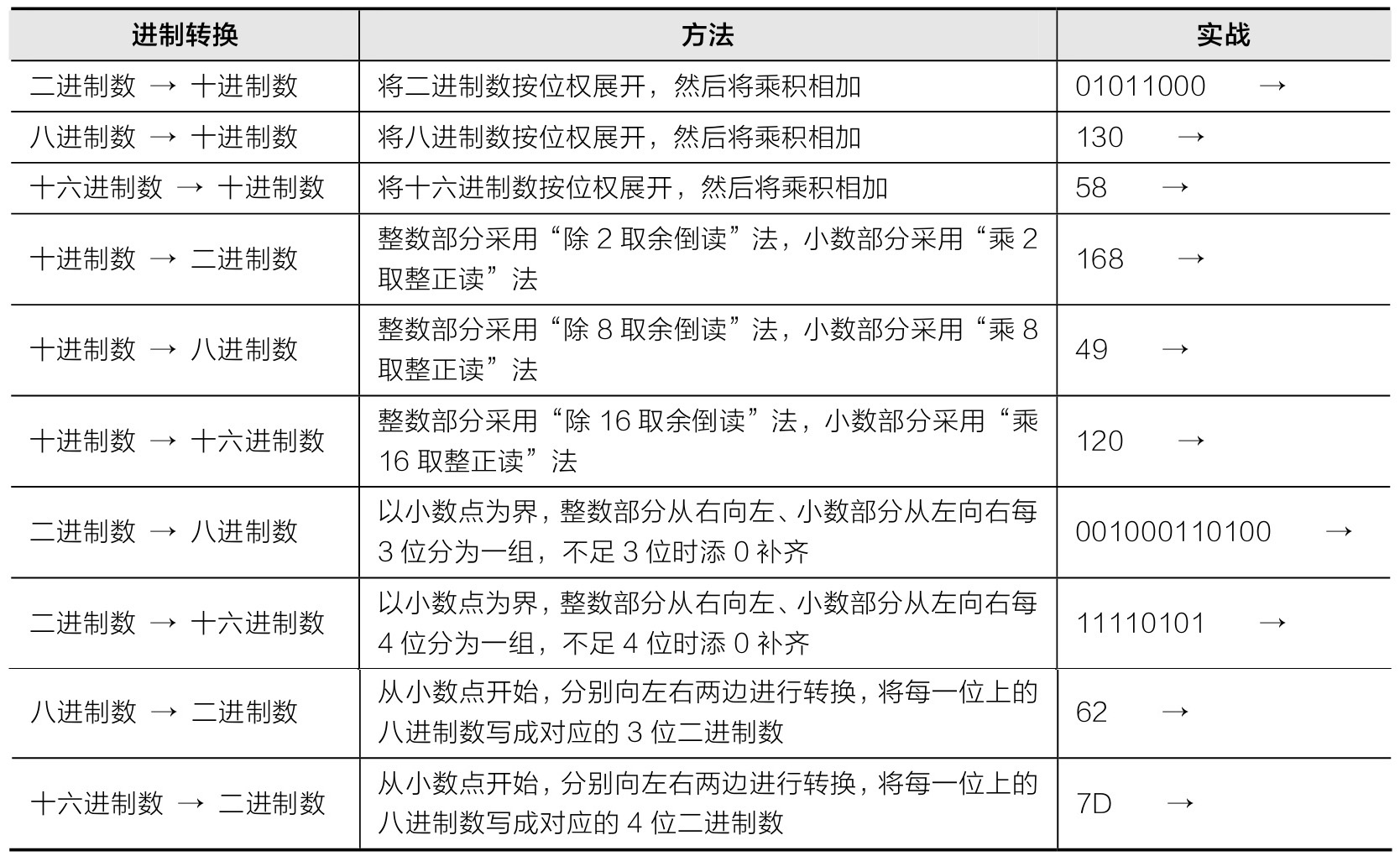
不同进制数字之间的转换是有一定规律的。本任务将带领读者进一步巩固这些转换规律,让大家能够更熟练地进行进制转换。请先熟悉表1-3中各种进制的转换方法,然后将指定的数字转换为要求的进制。
表1-3 不同进制的转换方法
多媒体技术是将文本、图像、动画、音频、视频等多种媒体信息通过计算机进行数字化加工处理,使多种媒体信息建立逻辑联系,并实现实时信息交互的系统技术。多媒体技术的特点非常鲜明,它不仅能够极大地提高处理效率,也更利于数字媒体的传播、分享和管理。多媒体技术能够实现人机互动效果,让大众接收信息的方式从被动变为主动,这样更利于信息的传播和接收。同时,多媒体技术能够将多方位的、多层次的媒体对象,如文字、图像、音频、视频、动画等结合起来,极大地提升数字媒体作品的质量,丰富数字媒体作品的形式。多媒体技术给人们带来的影响非常大,请查询资料并结合自身了解,将多媒体技术给人们带来的影响归纳到表1-4中。
表1-4 多媒体技术给人们带来的影响