




开普勒和第谷合作期间的第一个主攻目标就是火星轨道。研究刚开始的时候,开普勒认为攻克这个任务并不难,但是实际却越做越难。他艰苦卓绝地和火星对抗,过去的他用大胆的先验思辨来设想整个宇宙体系的结构,现在的他“汗流浃背,气喘如牛地跟踪着造物主的足迹”。开普勒在历练中逐渐蜕变为一位用实测数据探索其中所隐含的实验性定律的实践家,而他曾经的猜想由于存在缺陷而被他搁置。
火星在西方以战神(Mars)命名,开普勒总是把探索火星运行规律想象成他和战神之间的战争,他屡战屡败屡败屡战,可以说火星既是开普勒人生中的炼狱,又是他的福星。在数次失败后,他回头转身,暂时放弃进攻火星,开始研究地球的运行律。在第谷庞大的天文数据背后,开普勒凭借其天才的洞察力挖掘出了“矢径”这一概念,也就是“日地距离”的连线——虽然这条线实际并不存在。当实践家开普勒用第谷的实测数据,花了九牛二虎之力逐一计算得180个“日地距离”后,便开始进一步探讨这一大堆实算数据背后是否会有覆盖所有行星的精简的实验性定律。《新天文学》30章所列地球绕日运动,从远日点(0°)开始一直到近日点的角度(180°)的日—地距离 r 如下表所示(地球绕日运动对于近日点和远日点连线成轴对称,取此对称轴之半为100 000个单位长):
表1—1 从远日点到近日点的日一地距离
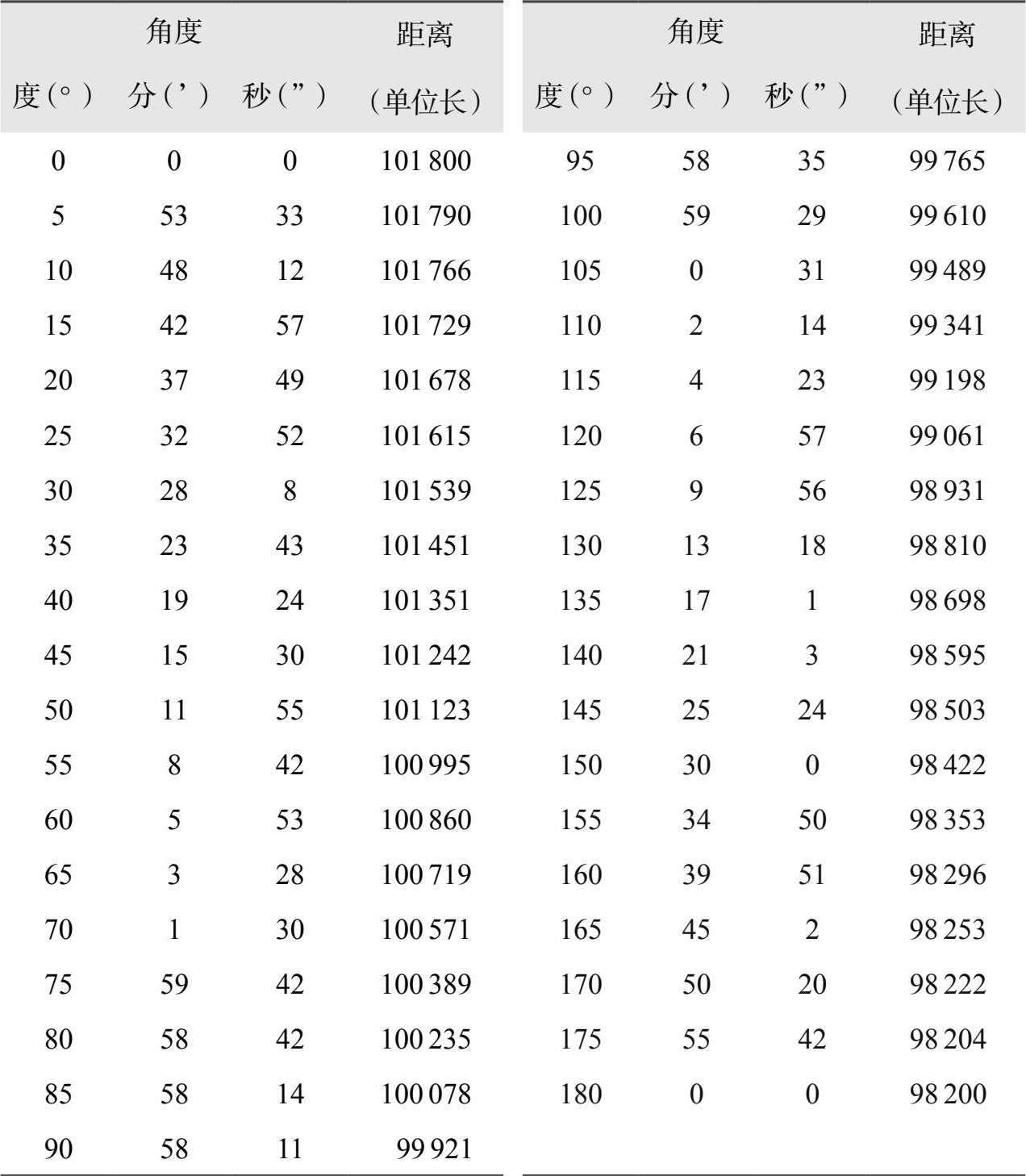
当时的天文学家熟知日—地射线方位的每天变动,即角速度 ω 。测量方法是用某一时刻日—地的方位和隔天的方位差得出每天的角速度。角速度 ω 是实测量,他们还知道近日点的角速度最大,远日点的角速度最小。在近日点、远日点的速率 v 显然等于日地距离 r 乘以角速度 ω ,即 rω 。开普勒根据数据表一眼就看到在近日点、远日点,他所算得的距离和速率成反比,随即猜想 rv 守恒。但是他马上发觉事实并非如此。后来他才领悟到那是因为地球绕日运动并非完美的圆周运动,也就是 v 不总是等于 rω 。通过比对实算数据 r 2 和实测数据ω,开普勒发现了一条简单的法则——面积律,即地球与太阳连线在相同时间扫过相等面积,其实就是 r 2 ω 的守恒律(注1)。由于当时还没有微积分这个工具,随后的推导过程是缘于他想起了公元前3世纪的古希腊数学家阿基米德曾用过的处理方法。就这样开普勒先得出了他的“第二定律”。
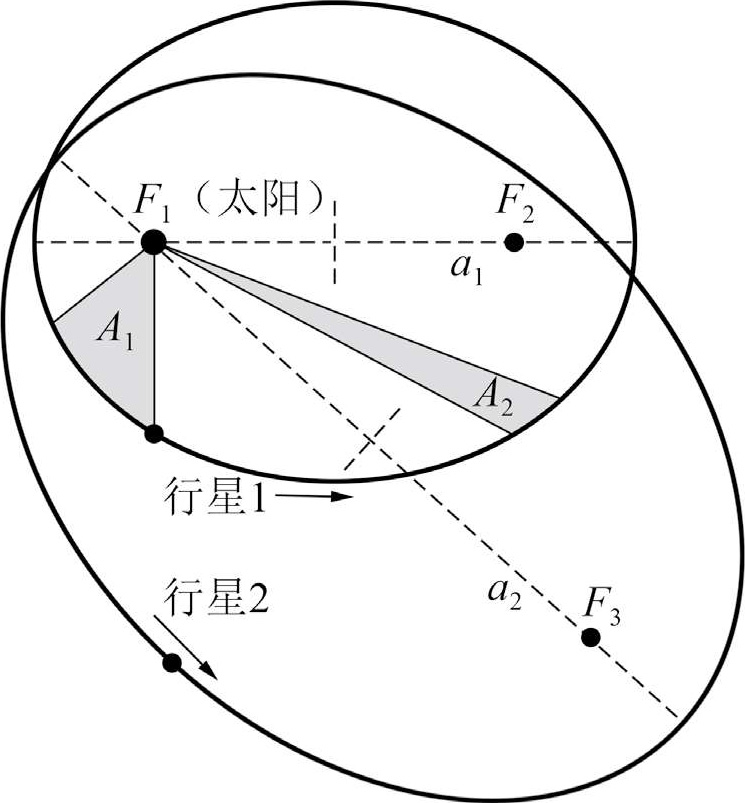
图 1-10 遵守开普勒行星运动定律的两个行星轨道