




1571年,本章的主角开普勒在德国中部符腾堡州魏尔德施塔特的一个贫困家庭出生。开普勒的童年十分凄惨,父亲是个对家庭很不负责的职业军人,母亲性情暴躁古怪。3岁时他又染上了肆虐欧洲的天花,不仅毁坏了面容,还使得一只手半残,视力也受到损害。而父亲的去世犹如雪上加霜,使得他饱受穷苦之累,有时只能乞住在乡村旅店之中。9岁时为了生活,他就开始做佣人,直到12岁才幸得他人帮助回到学校。
童年的苦难在开普勒的心灵上留下了深深的伤痕。幸好他没有被苦难击倒,反而因此磨炼了意志。他从小就喜欢到教堂做祷告,因为教堂那高高的圆形穹顶,管风琴美妙的和声,给苦难中的开普勒带来了温暖和希望。
凭借天赋和刻苦,开普勒17岁时进入了蒂宾根大学,他出众的数学才能很快得到认可,受到了数学教授马斯特林的赏识,而马斯特林就是一位哥白尼日心说的拥护者。当时在天文学界日心说和托勒玫的地心说是争论不休的热门议题,开普勒就曾经以日心论者参加这场辩论。虽然他当时在蒂宾根大学神学院学习,且以全班第二名的优秀成绩毕业,但由于信奉被教会视为洪水猛兽的哥白尼日心说,他失去了担任教会职务的资格。也许冥冥之中自有天意,上帝关上了一扇门却为开普勒打开了另一扇窗,1594—1595年的两起偶然事件使得开普勒踏上了研究天文学的漫漫征程。
1594年,奥地利格拉茨一所高中因一位数学教师突然病故,迫切地向蒂宾根大学的教授团求助,希望为该校推荐一位能胜任的继任者,在马斯特林的帮助下,开普勒被认为是适合人选。因此当年原本想以传教士为职业的开普勒改行到格拉茨当上了数学教师,同时,兼职天文学教师。从此他把当牧师的想法抛到了九霄云外,一心一意地开始研究行星问题。
在任教期间,开普勒最感兴趣的问题是:为什么行星有6颗(当时只发现了6颗行星)?它们的轨道半径为什么恰好成8∶15∶20∶30∶115∶195这样一个比例?他开始时试着用平面几何图形的组合来推出行星轨道,结果失败了。1595年7月19日,另一个偶然事件发生了。开普勒在天文课课堂上突发灵感:“行星在空间中运动,我怎么在平面上研究这些几何图形呢?应该用立体图形!”思路一开,很快就有了可喜的突破。当时人们知道5种正多面体,古希腊数学家还证明过,大自然只可能有5种正多面体。柏拉图在《蒂迈欧卷》里说,这5种规则多面体是“神的形象的天体”。开普勒接受了这种观念,并说:“我企图证明,上帝在创造宇宙和规定宇宙秩序的时候,曾考虑到5种规则的几何立体,他按照它们的大小,确定天体尺寸、数目、比例及其运动关系。”

图 1-7 开普勒位于魏尔德施塔特的出生地
开普勒的设想是,如果把5种正多面体和6个球形套合起来,不就有6个球吗?6个球的半径恰好对应6个行星的轨道。这实在是妙极,开普勒相信这就是只有6个行星的奥秘所在。开普勒的具体方法是这样的:开始以一个球形作地球的轨道,在这个球形外面配一个正12面体,这个正12面体的12个面与球形相切,12面体外面作一个圆球,这个圆球是火星的运动轨道;火星球外面作正4面体,再在它外面作一个圆球,得出木星轨道;木星球外作一个立方体,立方体外面的球就是土星轨道;在地球轨道的球形内作正20面体,20面体内的球形是金星的轨道;金星球内作正8面体,其内的球就是水星的轨道。根据这种方法得出各轨道半径的比,与观测结果大体相同(差别在5%以内)。开普勒十分兴奋,1596年底,他把他的这一发现写进了他的处女作《宇宙的奥秘》。
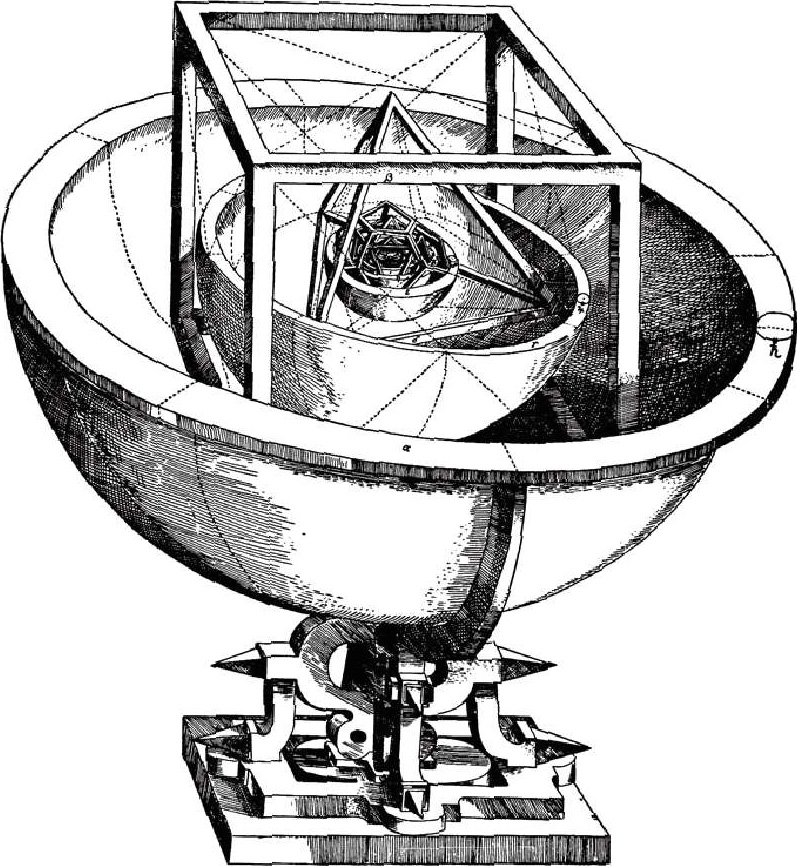
图 1-8 开普勒宇宙秘密模型