勒让德出生于法国巴黎,他在数学上贡献颇多,涉及的领域有椭圆积分、数论、初等几何和天体力学等等。勒让德家庭富裕,最初他可以全职从事科学研究,直到法国大革命的艰苦环境使他耗尽了家产,不得不以担任各种行政职务的小官为生。勒让德在马扎林大学接受教育直至1770年毕业。1775—1780年间,他在军校教授数学,这一时期勒让德出版的大地测量学著作相当重要,它被载入了托德亨特的《引力数学理论史和地球形状》。因此科学院委派勒让德进行重要的大地测量,比如1787年由格林尼治天文台和法国巴黎联合启动的一次工作。1791年,科学院再次提名勒让德和其他几人确定米的长度,以形成一个新的十进制测量系统的基础。然而,勒让德于1792年3月辞去了这个委员会的职务。1799年,拉普拉斯成为内政部长,勒让德接替他担任炮兵团学生的数学考官。在第三次反法同盟战争期间,年过半百的勒让德出版了他的《计算彗星轨道的新方法》一书,在书中他首次描述了最小二乘法的基本方法,他对最小二乘法的推导是完全属于代数的,没有统计的内容。总的来说,勒让德是一个杰出的数学家,而不是统计学家。1833年,勒让德于巴黎去世 [2] 。

图 4-2 勒让德
从统计史上来说,最小二乘法问题的提出来自求解线性矛盾方程组。用现在的术语来说,线性矛盾方程组是源于线性模型参数的估值问题。至于线性模型本身,则是来自天文和测地领域的误差分析中的一系列问题。相较于测地学,天文学是首先出现许多关于测量的误差问题的学科,因为科学的起源就在这里。从开普勒时期的天文学革命至19世纪天文学,这里一直是数学应用最频繁的领域。到了18世纪末19世纪初,天文学迅速发展,在此过程中积累了大量的数据需要分析,应该如何来和数据中的观测误差打交道成为那个年代一个数学家要面对的重要问题。其中的一些数据分析问题可以描述于下:
有若干个我们想要估计其值的量 θ 1 ,…, θ k ,另有若干个可以测量的量 x 0 ,…, x k 。按理论,这些量之间应有线性关系
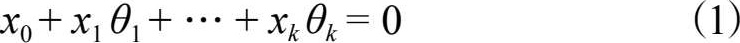
但是由于在实际工作中对 x 0 ,…, x k 的量测不可避免有误差, 加上式( 1 )本来就只是数学上的近似而非严格成立,式( 1 )左 边的表达式实际上不为 0 ,其实际值与量测有关,可视为一种 误差。现假设进行了 n 次观测, n ≥ k ,在第 i 次观测中, x 0 ,…, x k 分别取值 x 0 i ,…, x ki ,按式( 1 ),应有

根据线性代数,我们知道,如果不多不少 n = k ,则由方程组(2)唯一地解出 θ 1 ,…, θ k 之值,可以取它们作为 θ 1 ,…, θ k 的估计值。但当 n > k 时该怎么办呢?如果式(2)严格成立,则只要从这几个方程中任挑出 k 个去解就行,但如上面所讲的原因,式(2)实际上并非严格成立。因此,取不同的 k 个方程可能解出不同的结果。在实际问题中, n 总是大于甚至是远大于 k ,这是为了多提供一点数据信息以便对未知参数 θ 1,…, θ k 做出较精确的估计,这就是当时的天文和测地学家面临的数据分析问题。那应该如何操作?不同的数学家有不成系统的独到做法。
……
令人唏嘘的是,即使天才如欧拉和拉普拉斯这样的杰出数学家,也对解线性矛盾方程组这样一个貌似并非特别艰深的问题束手无策。个中缘由大概是,他们对数学的认识局限于求解那种一板一眼的纯数学问题,而并非像矛盾方程组这种在当时看来奇奇怪怪的问题。它的叙述方法和以往的数学问题不同,是一个新式的数据分析问题,需要一点新的想法。勒让德的成功在于他从一个新的角度来解决这个问题,他不像欧拉或是拉普拉斯那样致力于找出几个独立方程,其中最好的情况是方程的个数等于未知数的个数,然后再用现在本科生都熟悉的线性代数去求解,而是考虑误差在整体上的平衡分布,即不使误差大部分地集中在几个方程内,而是让它比较均匀地分布于各方程,这个考虑使他采取使的原则去求解 θ 1 ,…, θ k 。这段数学史也启发我们,历来数学观念上的突破、数学认识的革新、数学问题的解决是如何的不容易!但是一经点破,我们会感到事情是理当如此,我为什么会没有想到?但在没有发现以前,许多数学家大哲人努力了几十年也无功而返。 [3]