





图 3-19 瓦尔德
1902年,瓦尔德在罗马尼亚的克罗日出生。他是正宗的犹太人,先就读于克罗日大学,1927年进入了维也纳大学,在这里他进修了三门课程,其中包括统计学和经济学,1931年他获得了博士学位。因为政治上的原因,他没能找到很好的工作,只能给一位银行家当数学家教。不过正是因为这样,他对经济学产生了浓厚的兴趣。在第二次世界大战之前瓦尔德去了美国,后进入哥伦比亚大学学习数理统计学。
第二次世界大战是飞机战的开端,谁抢到了制空权,谁就占据了主动。战争期间,几乎每天都有大量飞机参战。于是问题就来了,飞机中弹乃至失事再正常不过,该怎么提高飞机的存活率呢?1943年,美国空军就如何加固飞机来咨询统计学家瓦尔德。因为飞机能够搭载的护甲有限,所以需要选择性地合理分配护甲。当时美国人一贯的做法是将护甲装在飞机机翼和尾部。空军负责人说,选择这些部位搭载护甲是因为那些顺利返航的飞机的这些部位布满了弹孔。瓦尔德意味深长地说:“这么做是不对的”。这些完成任务的飞机在机翼和尾部布满了弹孔,说明飞机被命中这些部位后,它仍然能工作,至少它返航了。瓦尔德随即问道:“那些被命中其他部位的飞机最终到哪里去了?”空军负责人哑口无言,显然它们一去不返。瓦尔德立刻给出了结论,应该在那些顺利返回的飞机没有弹孔的部位加固护甲。这就是有名的“幸存者偏差”。这一理论在今天仍然有着很强的现实意义,我们瞬间就可以理解幸存者偏差,比方说你发现一些没读过书的人很有钱,事实上是你发现的这些“不读书却很有钱的人”是幸存者,而大部分“死亡”的人你都见不到。
随着战争的深入推进,数理统计研究出现了一些重要的新方向,其中最有影响力的是瓦尔德的“序贯分析”和“统计决策理论”。瓦尔德之所以研究出序贯分析这种崭新的统计方法,是二战中军需验收工作的需要。1947年,瓦尔德发表了《序贯分析》专著,使得序贯分析成为数理统计学中一个新的重要部分。之前,人们在统计推断中一般使用的是“固定抽样方案”,即事先确定抽样个数的抽样方案(注5)。而序贯分析则是分步抽样:先抽少量样本,根据结果再决定是停止抽样还是继续抽样以及抽多少样本,然后将得到的样本进行统计推断。在这个方法提出之前,抽样的多少一般在统计之前就已经被确定下来。应用“序贯抽样方案”可以节省很多资源,因为它可以在统计过程中根据具体情况对抽样的多少进行判断。比如,当统计推断得到的结果已经很精确的时候,可以停止抽样。1950年瓦尔德还发表了著述《统计决策函数》,标志着他创始了统计决策理论,即将统计推断所获得的论断会产生什么后果,应采取怎么样的对策或行动也纳入统计范围内,用与大自然博弈的观点看待数理统计问题。其基本思想是人们最初可以根据主观猜测来确定世界状态的概率分布,但是,随着对世界状态的客观知识的增加,人们应根据这些新知识并借助贝叶斯概率公式不断地修正主观概率,以使主观概率逐渐转化为客观概率,根据客观概率的大小进行决策分类,从而使人们的决策更为可靠。不过可惜的是,在出书的同一年,瓦尔德因为乘坐的飞机失事,不幸去世。
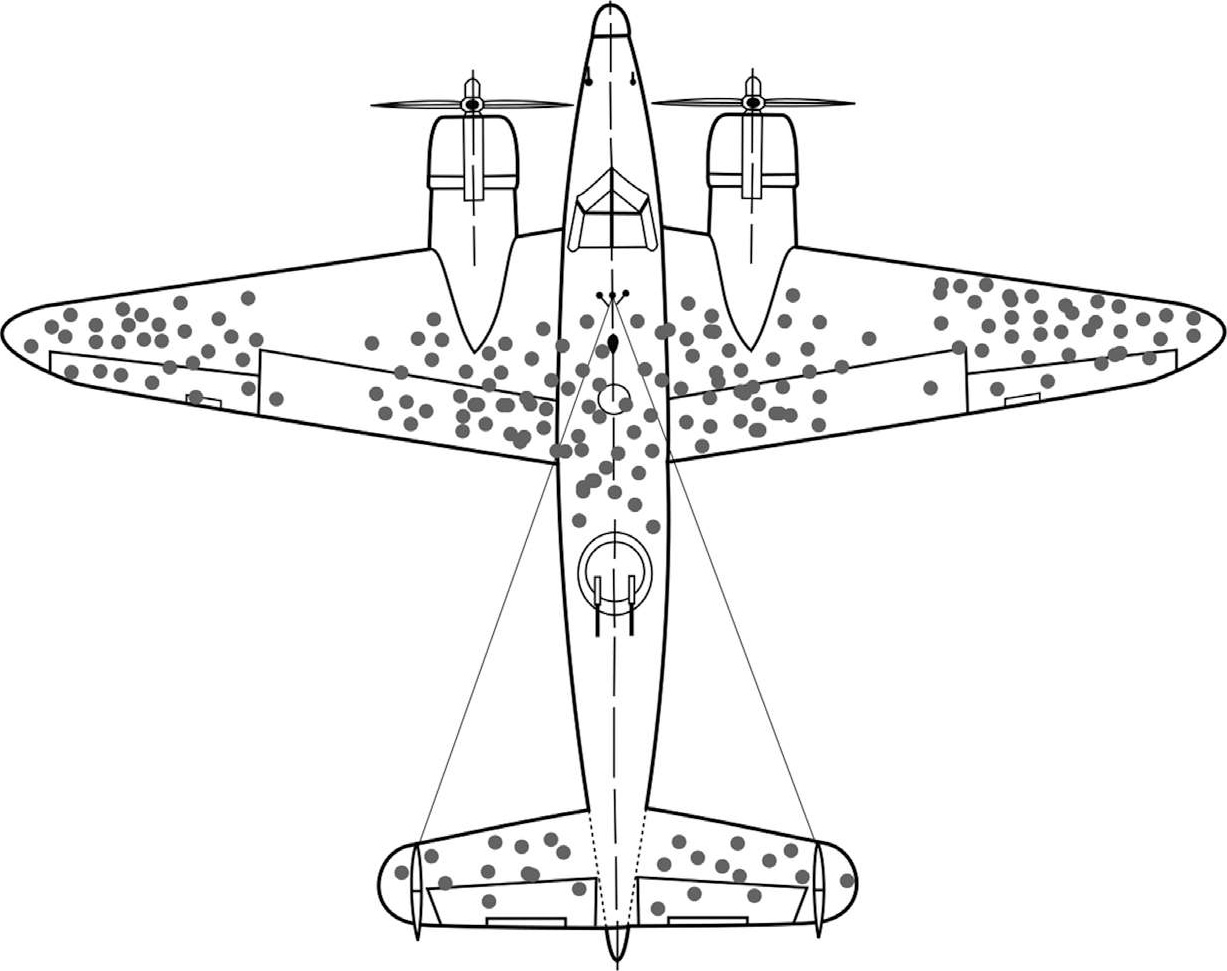
图 3-20 返回基地的飞机上弹孔的位置

图 3-21 萨维奇
另一位和瓦尔德同时代的杰出贝叶斯主义者萨维奇把概率看成了是私人的事情,他拓展了拉姆齐和菲耐蒂的主观概率理论,建立了规范人们行动的主观期望效用理论。萨维奇指出,概率是决策理论中一个基本的概念,而效用则是另一个基本概念(注6)。由于概率反映了决策者实际的信念,这种概率是主观的,效用则反映了决策者的价值观念、向往或期望,因此效用也是主观的。萨维奇的主观期望效用理论是把贝叶斯学派的归纳理论应用于实际的结果。该决策理论主张个体的概率分布由行动的偏好决定,理性人的行动选择应该遵循主观期望效用的最大化。但是,该理论也遭受了不少批评和挑战,最著名的例子是阿莱斯悖论 [17] 和埃尔斯伯格悖论 [18] 。这两个悖论指出,在现实生活中,人们实际行动的选择并不总是和该理论的结果相一致,人们并不总是按照主观期望效用最大化进行决策。虽然阿莱斯悖论和埃尔斯伯格悖论不是严格意义上的逻辑悖论,但是它们表明了在不确定情形下,行动决策存在非理性。这使得经济学家开始对完全理性人假设进行重新审视,决策研究开始重视非理性因素的作用。因此,在萨维奇的主观期望效用决策理论遭遇悖论挑战后,主观决策理论开始朝两个方向发展。一是继续坚持理性决策宗旨,或对现有的期望效用理论进行改进,或研究更具普遍性的理性决策理论;一是质疑期望效用理论本身,开始研究行为人行动时的心理因素。毫无疑问,这对促进决策理论的发展起到了极大的作用 [19] 。
瓦尔德和萨维奇提出的这些理论与当时“统计学界的恺撒”费希尔的理念相违背。费希尔认为,统计学的任务是进行数据分析、获取相应的信息,而不是做出决策,他尽量避免使用先验分布。相反的是,瓦尔德在进行统计推断时,提倡使用先验分布和贝叶斯定理,由此引起了很多学者的关注。以至于在20世纪下半叶,统计学家们分成经典学派和贝叶斯学派,对贝叶斯统计及其先验分布进行了激烈的讨论。两派之间一直存在着各种争议,不过这对数理统计不仅没有坏处,还激励了其发展。