




首先,联合概率是可交换的,即 P ( AB )= P ( BA ) (1)
然后按条件概率的定义展开为乘法公式, P ( AB )= P ( A ) P ( B | A )
同理, P ( BA )= P ( B ) P ( A | B )
所以由(1)可得下面的表达式:
P ( B ) P ( A | B )=P( A ) P ( B | A ) (2)
式(2)变形得到:
P ( A | B )= P ( B | A ) P ( A )/ P ( B ) (3)
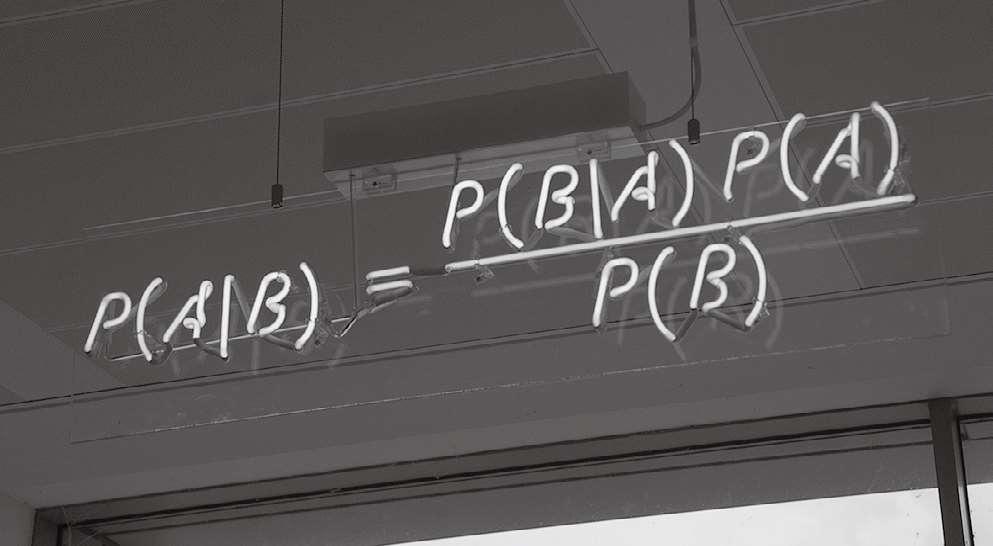
图 3-8 贝叶斯公式
我对贝叶斯公式感触最深的还是茆诗松老师在《概率论与数理统计教程》里的一道例题,《伊索寓言》里的《狼来了》。

图 3-9 《伊索寓言》中《狼来了》的插图
一个小孩每天上山放羊,山里有狼出没。第一天,他在山上喊:“狼来了!狼来了!”山下的村民闻声都去打狼,可到山上发现狼没来;第二天仍是如此;第三天,狼真的来了,可无论小孩怎么喊叫,也没有人来救他,因为前两次说了谎,人们不再信他了。这里 A 是“小孩可信”, B 是“小孩说谎”。 A 是我们希望了解其发生概率的现象, B 是我们希望与现象 A 联系起来的现象。
P ( A | B )是发生 A
P ( B | A )是发生 A
这里假设村民对小孩的印象 P ( A )=0.8, P (┐ A )=0.2。我们现在来求 P ( A | B ),就是这个小孩说了一次谎后村民对他的可信度的改变。在求 P ( B )时用到全概率公式(注2):
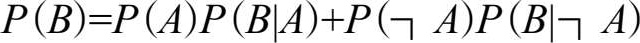
不妨设“可信”( A )的孩子“说谎”( B )的可能性 P ( B | A )=0.1,“不可信”(┐ A )的孩子“说谎”( B )的可能性 P ( B |┐ A )=0.5,则 P ( B )=0.18。第一次村民上山打狼,发现狼没来,就是小孩说了谎( B ),村民根据这个信息,对小孩的可信程度改变为:
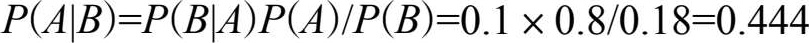
这表明村民上了一次当后,对这个小孩的可信程度由原来的0.8调整为0.444,也就是新的 P ( A )=0.444, P (┐ A )=0.556。在此基础上,我们再一次计算 P ( A | B ),也就是这个小孩第二次说谎后,村民对他的可信程度变为:
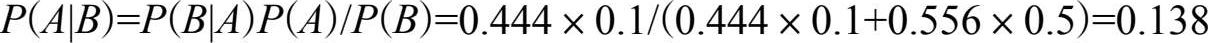
这表明村民经过两次上当,对这个小孩的可信程度已经从0.8下降到了0.138,如此低的可信度,村民听到第三次呼叫怎么会再上山呢?
这个故事用到的原理正是贝叶斯定理,当年贝叶斯在摆弄条件概率公式时惊奇地发现,这些公式都是内部对称的!以“前事件”为条件讨论“后事件”的概率一直以来都是有意义的,而以“后事件”为条件计算“前事件”发生的概率居然也是可行的。这个定理看起来不起眼,却一举解决了以“后事件”推测“前事件”的“逆概率”问题。下面几节它会显示出更强大之处,且耐心听我一点一点慢慢道来。
首先改变一下定理的形式,将之推广到具有多个独立同分布(注3)的可观测随机变量 X 1 , X 2 ,…, X n ,每一个变量有概率密度函数 f ( x | θ )。也就是说, f 代表了一个随机向量 X 的密度,它以另一个随机变量 Θ = θ 为条件。假定 θ 是不可观测的,而 θ 代表了 Θ 取定的值。 g ( θ )为 Θ 的概率密度函数。那么,贝叶斯定理变为:
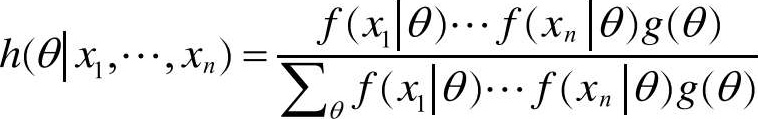
这里, h 被称为 θ 的后验概率密度函数。
证明很简单,只需利用条件概率定义和全概率公式,在此不再赘述。
我们来看上式,由于分母只依赖于 x i ( i =1,2,…, n ),而不是 θ ,上式可以表示为:
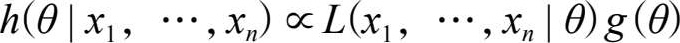
符号∝表示成比例,而
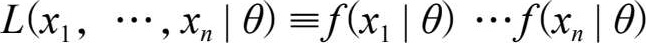
表示参数 θ 给定后数据的“似然函数”(“似然”的字面意思是“看起来像”。“似然”可以理解为“可能性”,“似然性”与“概率”意思相近,都是指某种事件发生的“可能性”,但是在统计学中,“似然性”与“概率”又有明确的不同。“概率”用于在已知一些参数的情况下,估计后面观测会得到的结果。而“似然性”则是用于在已知某些观测所得到的结果时,对参数进行估计),其中各数据 x i ( i =1,2,…, n )是相互独立的。当 L 被看作 θ 的一个函数时,似然函数是唯一的,仅相差一个乘积常数,该常数在贝叶斯定理中不加区别。 g ( θ )被称为 Θ 的先验概率密度函数,这是由于 g ( θ )是在当下实验观察 X 之前确定的。也就是说, g ( θ )是以过去的实践经验和认识为依据的。 h ( θ | x 1 , x 2 ,…, x n )被称为 Θ 的后验概率密度函数,这是因为 h 是在观察了当下数据之后才确定的。所以贝叶斯定理的等价表述为:
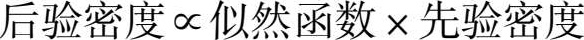
贝叶斯定理告诉我们,如果没有当下观测值可以利用,那么我们就必须根据以前的经验对 θ 做出一切判断,即我们仅使用先验概率密度函数 g ( θ )。如果我们既有以前的经验,又有依据观察数据的当下认识,我们就可以利用贝叶斯定理修订 g ( θ ) [8] 。