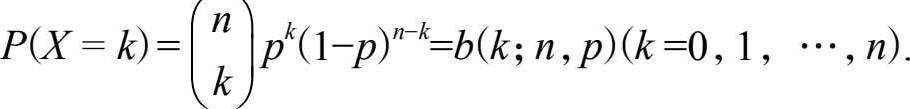注 1:伯努利试验
伯努利试验是只有两种可能结果(事件 A 发生或不发生)的随机试验。该试验在同样的条件下重复地、相互独立地(事件 A 发生或不发生对事件 B 不产生影响,就说事件 A 与事件 B 之间存在某种“独立性”)进行 n 次,那么就称这一系列重复独立的随机试验为 n 重伯努利试验。
注 2:伯努利分布
这里或许我们先要解释一下“概率分布”以及“概率密度”为何物。首先我们要提到“随机变量”,简单来说,随机变量指的是“不能确定取值,但能确定取的值的概率的变量”。打个比方,在投掷骰子的时候“第一次出现的数字”(1到6的任何一个整数)就是一个随机变量。粗略来说概率分布指的就是随机变量以什么样的概率取什么样的值,这时的随机变量,我们称其“服从”这个概率分布。另外,我们也经常简称概率分布为“分布”。具体来说,比如掷正常的骰子,记 X 表示出现的点数,则 X 的可能取值为1,2,…,6。这是一个离散随机变量,在离散情况下这被称为“概率分布列”: P ( X =1)= P ( X =2)=…= P ( X =6)=1/6。如果是连续的情况,我们就称其为概率密度。下面我们记事件 A =“点数小于等于 x ”,可以表示成 A ={ X ≤ x }。我们取 x =1,2,…,6的任意一个值,则 F ( x )= P ( X ≤ x )就是概率分布: F (1)= P ( X ≤1)=1/6, F (2)=1/3, F (3)=1/2, F (4)=2/3, F (5)=5/6, F (6)=1。我们可以看到概率分布是概率分布列的逐步累加,在连续随机变量的情况下,概率分布就是概率密度的积分。如下图所示:
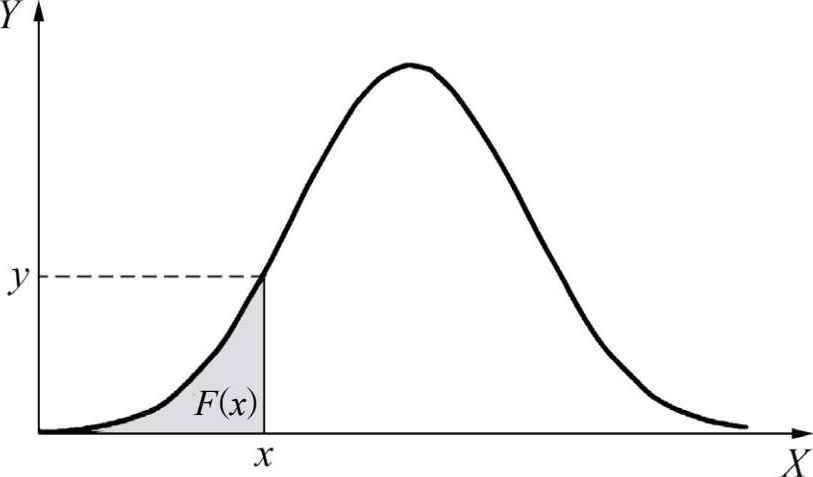
图 2-14 概率密度图(被覆盖的阴影部分面积表示概率)
伯努利分布,是一种离散分布,又称为“0—1分布”或“两点分布”。参数为 p 的伯努利分布主要用来描述一次伯努利试验中的一个事件的出现次数(0次或1次)。 [9] 所谓“参数”,在概率论和数理统计中指的是为某概率分布加上特征的数字,比如我们在说“参数服从 p 的伯努利分布”时,蕴含着“这个伯努利分布可以用1个数字确定”。
伯努利分布列为
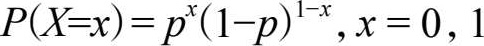
或记为

注 3:二项分布
二项分布就是重复 n 次独立的伯努利试验中表示一个试验结果发生次数的随机变量服从的分布。当试验次数为1时,二项分布服从0—1分布即注2中的伯努利分布。二项分布列为