




棣莫弗无疑是名垂青史的天才数学家。他出生在法国香槟省维特里—勒弗朗索瓦的一个小康之家。由于早年所读的学校里没有数学课程,他就在课外自习数学。大约在1684 年,他到巴黎的哈考特学院学习,才第一次接受正规的数学训练。但很快在当时法国的新旧教斗争中因自己的加尔文教派身份而被投入监狱。1688 年他出狱后去了伦敦,在那里结识了好友哈雷,就是那个计算出“哈雷彗星”轨道的哈雷,还有大科学家牛顿。牛顿对于棣莫弗的数学才能予以了高度赞赏。据说当人们向牛顿提出数学方面的问题时,牛顿经常回答说:“请去询问棣莫弗,这些问题他比我了解。”
棣莫弗如此名声在外,可是一生却苦难不断。由于他新教徒的出身,在英国只要不是国教徒(即天主教徒)就不可能获得教授的职位。棣莫弗曾著书出版,但微薄的版税收入还不够糊口。为了生活,棣莫弗除了给贵族子弟们开数学课,据说还去咖啡馆接受有关概率、保险和养老金的咨询。前来咨询的既有赌徒,也有保险从业者和养老金的销售者,他在咖啡馆过着有一顿没一顿的生活。

图 2-11 棣莫弗
1718年,棣莫弗出版了《偶然论》这部著作。这本书是那个时期集概率论成果之大成者,书中介绍了今天我们称之为“二项分布的正态近似”的内容。这一成果是棣莫弗在概率论上的最大发现。关于正态分布,我们将在第4章详细解说,那是测量误差的概率曲线,而棣莫弗的研究是出于一个完全不同的目的——计算二项分布(注3)的概率。棣莫弗在书中考察那些发生或不发生有着相同概率的事件,比如抛硬币,正面朝上或不朝上的可能性是相同的。在观察大量的此类事件中,棣莫弗感兴趣的是计算某一结果出现特定次数的概率。例如,当一枚硬币被抛掷多次时,计算正面出现次数的概率。让我们来分析这个问题,看看试验次数非常大时会发生什么情况。
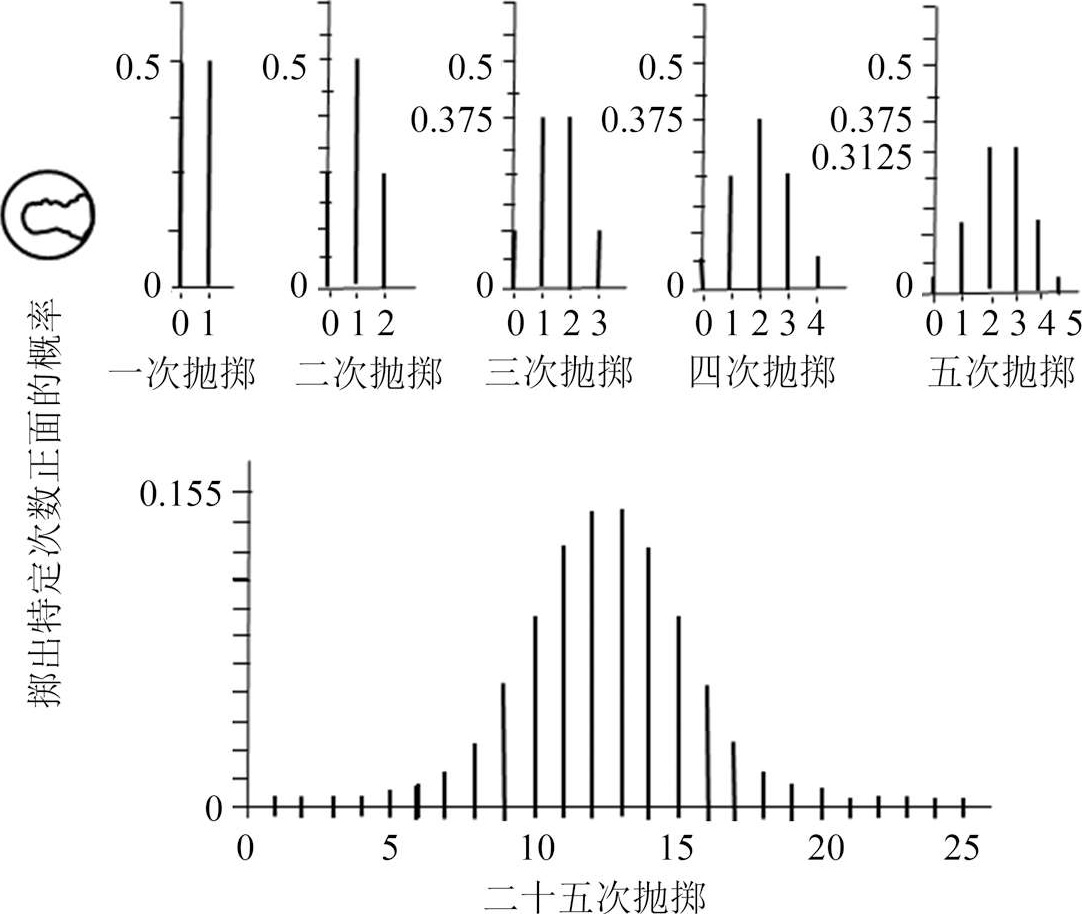
图 2-12 当一枚硬币被抛掷一次,两次,三次,四次,五次和二十五次时正面出现次数的概率
如图2—12,抛掷一次硬币时,我们能够得到总共0次正面(即一次反面)或1次正面。因为0次正面和1次正面这两个结果是等可能的,所以概率线条图显示出两条线段等高,表明概率等可能。当抛掷一枚硬币2次时,我们可能得到0次正面,1次正面,或2次正面。出现1次正面的概率是出现0次正面或2次正面概率的两倍。随着抛掷次数的增加,可以发现二项分布的模式逐渐向“钟形曲线”或者说“正态分布”靠近。
至此,古典概率论就告一段落了。由于牛顿和莱布尼茨创立了微积分,数学分析在18世纪开始逐渐发出耀眼夺目的光芒。之后分析概率论开始盛行,其标志就是拉普拉斯于1812年出版的《概率的分析理论》,这一阶段“中心极限定理”成为概率论舞台的中心。现代概率论受公理化数学潮流的影响,成了一门严密的数学学科。公理化方法就是从尽可能少的原始概念和一组不证自明的命题出发,利用纯逻辑推理法则,把一门数学建立成为一个演绎系统的方法。现代公理化方法的开端就是希尔伯特在其《几何基础》一书中对欧氏系统加以完善后,不仅在公理的表述或定理的论证中摆脱了几何学中空间概念的直观成分,而且给出和奠定了对一系列几何对象及其关系进行更高一级抽象的可能性和基础。通俗说来就是,几何学的点、线、面假使换成了桌子、椅子、啤酒杯,几何学也能成立。