




使用骰子、硬币的游戏曾在欧洲流行了2000多年,但直到15世纪末17世纪初,意大利的学者们才逐渐对概率产生了正确理解。虽然那时的赌徒们已经拥有了大量赌博知识,但直到卡尔丹和伽利略的著作出版,才展现出人类对概率的深刻见地。可惜的是,这门诞生于意大利的学问并没有在意大利本国开花结果,历史的使命落在了法国数学家的身上。
1654年,一位法国贵族梅雷把在赌场中遇到的难题请教伟大的数学家和物理学家帕斯卡。帕斯卡又把问题寄给另一位法国大数学家费马,之后在他们7封充满智慧的往来信件中,不仅各自独立而正确地解决了这个问题,还共同开创了概率的数学理论。1654 年 7 月29日,费马和帕斯卡的第三封通信被视为概率论的生日。他们信中究竟讨论了什么问题呢?其实就是帕乔利提出过的“分赌本问题”:有两个人,甲和乙,假定两人赌技相当,开始了一场公平的赌博,他们各出36枚金币共72枚作为赌注,赌局将在一个人赢过6轮后结束。赌博实际在甲赢5轮而乙赢4轮时中断。假定赌博过程中不存在平局的情况,此时应该如何分配赌金?

图 2-6 帕乔利
这是一个在数学史上非常著名的问题,在历史上曾经有不少解决方案,接下来就介绍其中最具代表性的四种:
方案A
分赌本问题的最早提出者帕乔利于1494年给出了解决方案。他根据已知条件,甲胜5局而乙胜4局,所以甲获得最终胜利的可能性较大。于是,可以根据甲乙两人胜局数之比,即5∶4来分配赌金。所以甲分到40枚金币,乙分到32枚金币。但之后1556年被同为意大利的数学家塔尔塔利亚发现了其中的错误:如果比赛停止时一个参加者赢了一局而另一个赢了零局,第一个人将拿走全部赌注,这显然是不公平的结果。
方案B
这一方案的提出者就是数学家卡尔丹,他思考:比赛若不中断,甲只需要再赢一局就可以获得最终胜利,乙则需要赢两局。显然,离开全胜所差的局数越少,获胜的可能性就越大。所以,可以考虑根据甲乙两人待胜局局数的反比,1∶2的反比,即2∶1来分配赌金。于是甲分到48枚金币,乙分到24枚金币。不难看出,卡尔丹已经开始意识到赌金的分配不应只依赖于已胜局,还应和赌徒离全胜所差的局数有关。然而待胜局是一个定值,比赛一旦继续下去胜负不能确定,因此他给的解答仍然欠缺一定的合理性,但朝着正确的方向迈进了一步。
方案C
这个方案的提出者是17世纪的“数学神童”法国人帕斯卡。帕斯卡生于1623年,父亲是一名贵族,对数学和科学有着很大的兴趣,母亲也很有教养。自幼帕斯卡就受到良好的家庭教育,而且天赋出众。1639 年当时只有 16 岁的帕斯卡就发表了《圆锥曲线专论》,其中记载了现在仍广为流传的“帕斯卡定理”。据说当时最著名的数学家笛卡儿简直无法相信这是一位16岁少年的成果。那之后又过了几年,帕斯卡发明了机械式加法器—近代现金出纳机的祖先。24岁时帕斯卡跨入欧洲大陆的科学界,完成了《有关真空的新实验》。此后一直到1653年,帕斯卡又作为先驱者之一开创了流体力学。

图 2-7 帕斯卡
1654年他与数学家费马通信,描述了他对分赌本问题的解法。他分析道:赌博中途停止了,比赛结果就不能确定了,双方都有可能获胜。此时甲离全胜只差一局,因此假设比赛继续进行,先增加一局,产生两种可能情况:要么甲胜,要么甲负。如果甲胜,他将赢得6局比赛,继而拿走全部赌金。如果甲负,此时甲乙胜局为5∶5,那么甲应该分得一半赌金。所以,在已知条件下,甲胜的话将分得72枚金币,甲负的话得到36枚金币。于是,帕斯卡认为可以这样分配赌金,先将赌金中的一半36枚金币分给甲,剩下的一半18枚可能甲得,也可能乙得,两人赌技相当获胜机会均等,所以甲得36+18=54枚,乙得18枚。赌金分配为3∶1。这一解法无疑是正确的,若干年后他在《论算术三角形》的末尾又做了更为详细的叙述。
然而就在当年,帕斯卡的信仰受到一个天主教派“冉森教派”的影响,对宗教有了些新的看法。在一次出行时,他所乘马车的马突然受惊狂奔,险些使他送掉性命。他把这件事解释为“神的不悦”,于是更坚定地信仰天主,这促使他把兴趣转向神学方面,将他短暂的、受疾病折磨的余生献给沉思默想、禁欲主义及宗教著述。从那时起直至去世,他都是在修道院中过着半僧侣式的生活。按照帕斯卡的观点,上帝或者存在或者不存在。对两个命题哪个为真,一个人只能进行“押宝”,这里押宝就是按照上帝存在与否来行事为人。帕斯卡分析道:如果上帝不存在,生前如何行事为人,结局都没区别;如果上帝存在,那押宝押在上帝不存在,生前放纵生活,最终就将被扔进地狱;如果押宝押在上帝存在,那你就会得到拯救。显然遵循上帝旨意生活的人结局要好多了。
让人颇为意外的是,即使如此帕斯卡在数学领域的发现也并没有完全止步于1654年。1658年的某个傍晚,帕斯卡觉得牙疼难忍,为了分散注意力,他决定全神贯注地研究一项当时许多数学家都关心的摆线难题。于是,牙疼完美地得到了抑制。帕斯卡认为这是一个好兆头,在那之后的整整8天他投身相关的问题,解开了不少当时无人可解的难题。
方案D
这个方案的提出者正是帕斯卡的好友,法国数学家费马。费马1601年出生在法国南部图卢兹附近博蒙—德洛马涅的一个富商家庭,父亲是皮革商人。费马在大学时专攻法律,毕业后成了一名律师,曾担任图卢兹议会的法律顾问三十余年。费马特别喜爱数学,他30岁时开始把业余时间几乎全部用于研究数学。他在数学和几何光学的许多领域都取得了丰硕成果,有“业余数学家之王”的美誉。大约是1637年,费马在阅读古希腊数学家丢番图的《算术》一书时,在书的空白处写下许多注释。其中一条注释说:“ 不可能把一个整数的立方分解为两 个立方数之和,也不可能把一个四次幂分解为两个四次幂之和,一般 地说,不可能把任意高于两次的幂分解为 两个同次的幂之和。对此,我已发现 了一个真正奇妙的证明,可惜这里 的页边空白太小,写不下了 。”他的这个注释在他去世三年后发表,人们为了纪念费马,把它称为“费马大定理”。经过三个半世纪的努力,这个数学史上最著名的数论猜想才由英国数学家怀尔斯和他的学生泰勒于1994年成功证明。

图 2-8 费马
回到分赌本问题,费马的这个方案堪称一绝。他在方案C的基础上,假设比赛继续进行下去,先增加一局,产生两种可能结果。如果甲胜,他将赢得最终比赛。如果甲负,此时甲乙胜局数比为5∶5,按照比赛规则还不能决出胜负。按照游戏规则,即便已经分出了胜负(如果甲胜)也要比完既定的次数,而费马所使用的技法正是如此。他尝试再增加一局比赛。结果如下:
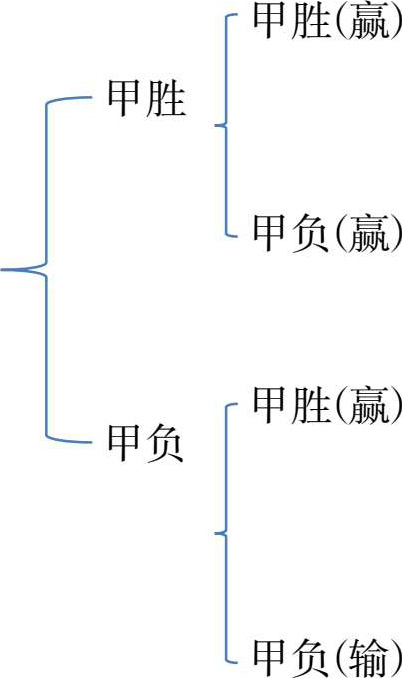
我们发现,在四种可能结果中,甲在前3种情况下都获胜,按约定应该获得全部赌金,只有在最后一种可能乙会获胜。因此,甲获胜的可能性为3/4,而乙为1/4。赌金分配为3∶1。
从以上4个方案中不难看出,方案A、B都是依据比赛停止之前已经进行的比赛结果来分配赌金,考虑的是既定事实。而方案C、D则是分析比赛所有可能的结果,考虑了最终比赛结果的随机性。至此,帕斯卡和费马各自从不同的观点出发,都给出了问题正确的解答,从而平息了分赌本问题在数学史上近两百年的争论。概率论这门新兴的数学学科也伴随着分赌本问题的发现、提出、分析、解决而诞生了。帕斯卡和费马的圆满合作使得他们建立了深厚的友谊,彼此欣赏对方的才华。在1660年7月的信中,费马热情洋溢地邀请帕斯卡会面,“我非常想热烈地拥抱你,并奢望和你聊上几天几夜”。在8月10日的回信中,帕斯卡表达了对费马的尊重,“一旦身体允许,我立刻会飞到图卢兹,绝不会让您为我迈出一步”。然而最终两人未能见面。